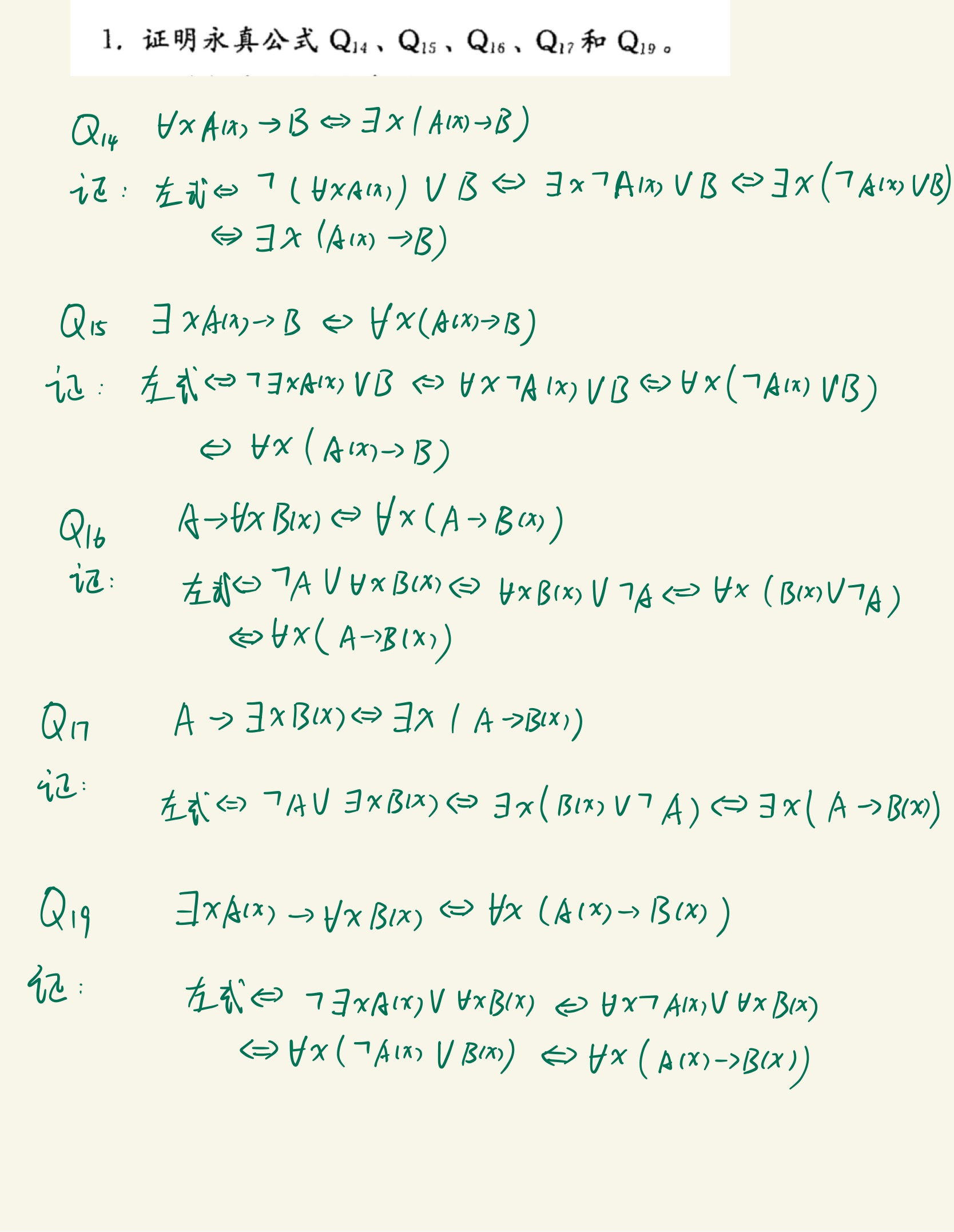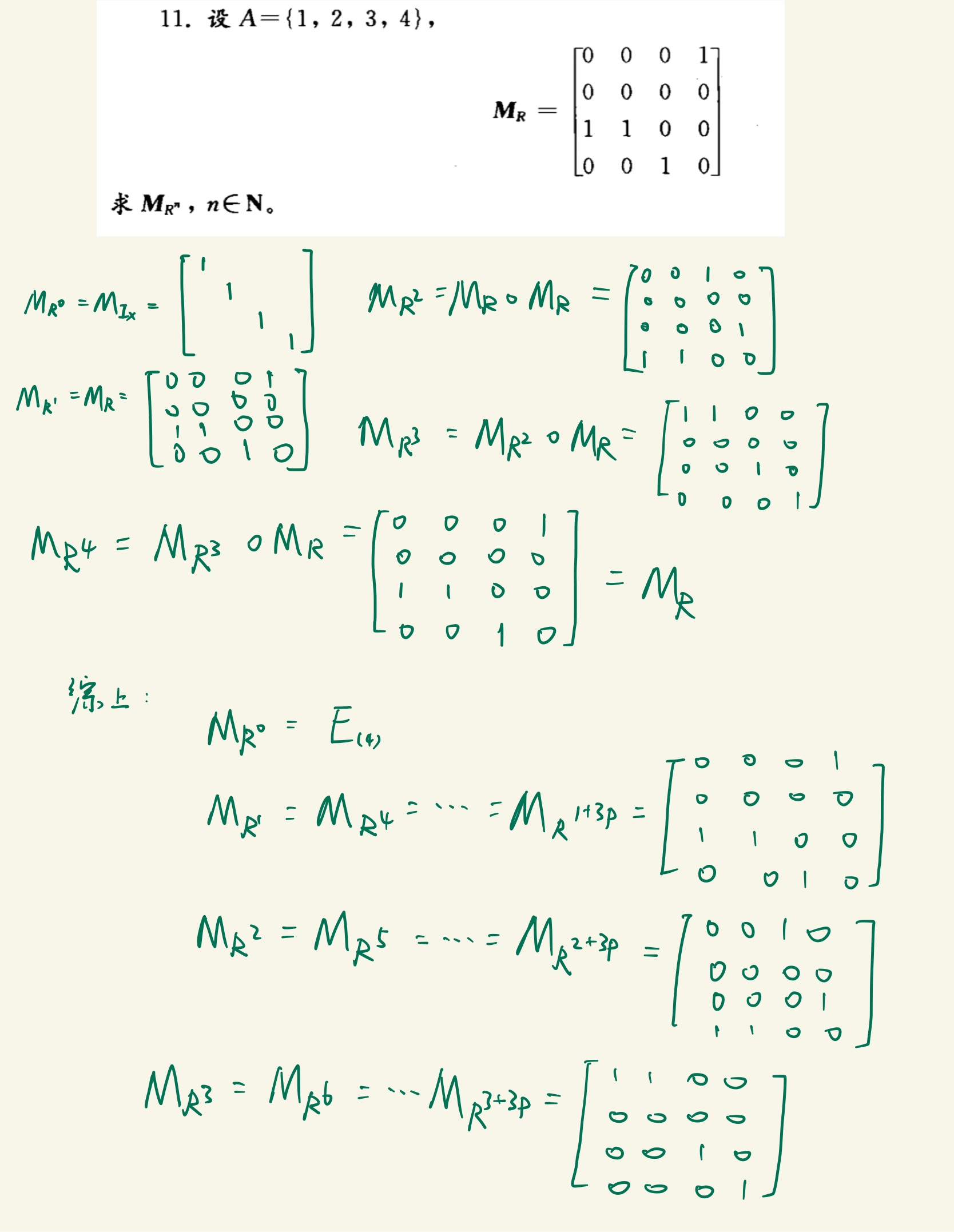离散数学笔记
先贴作业,笔记在后面。
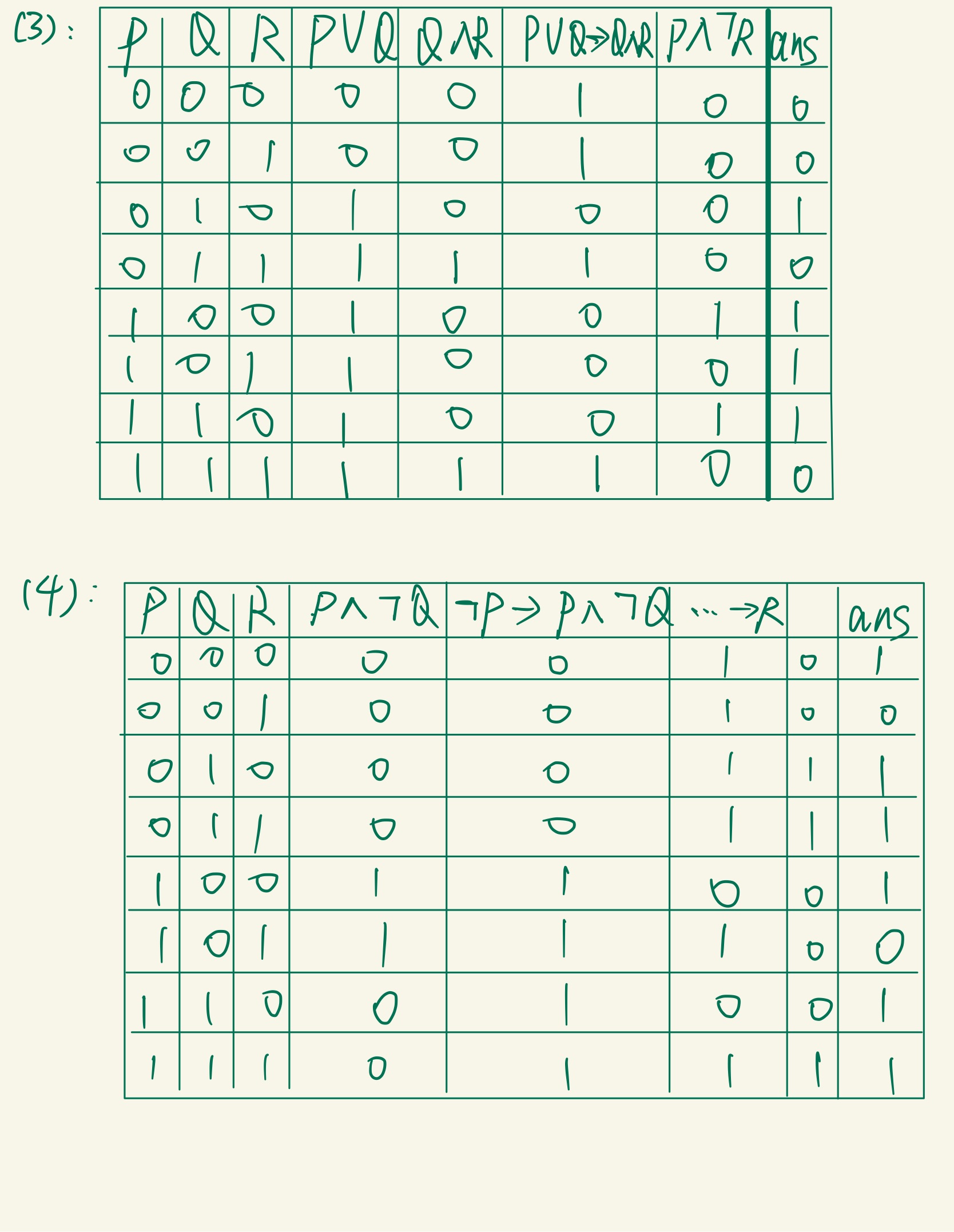
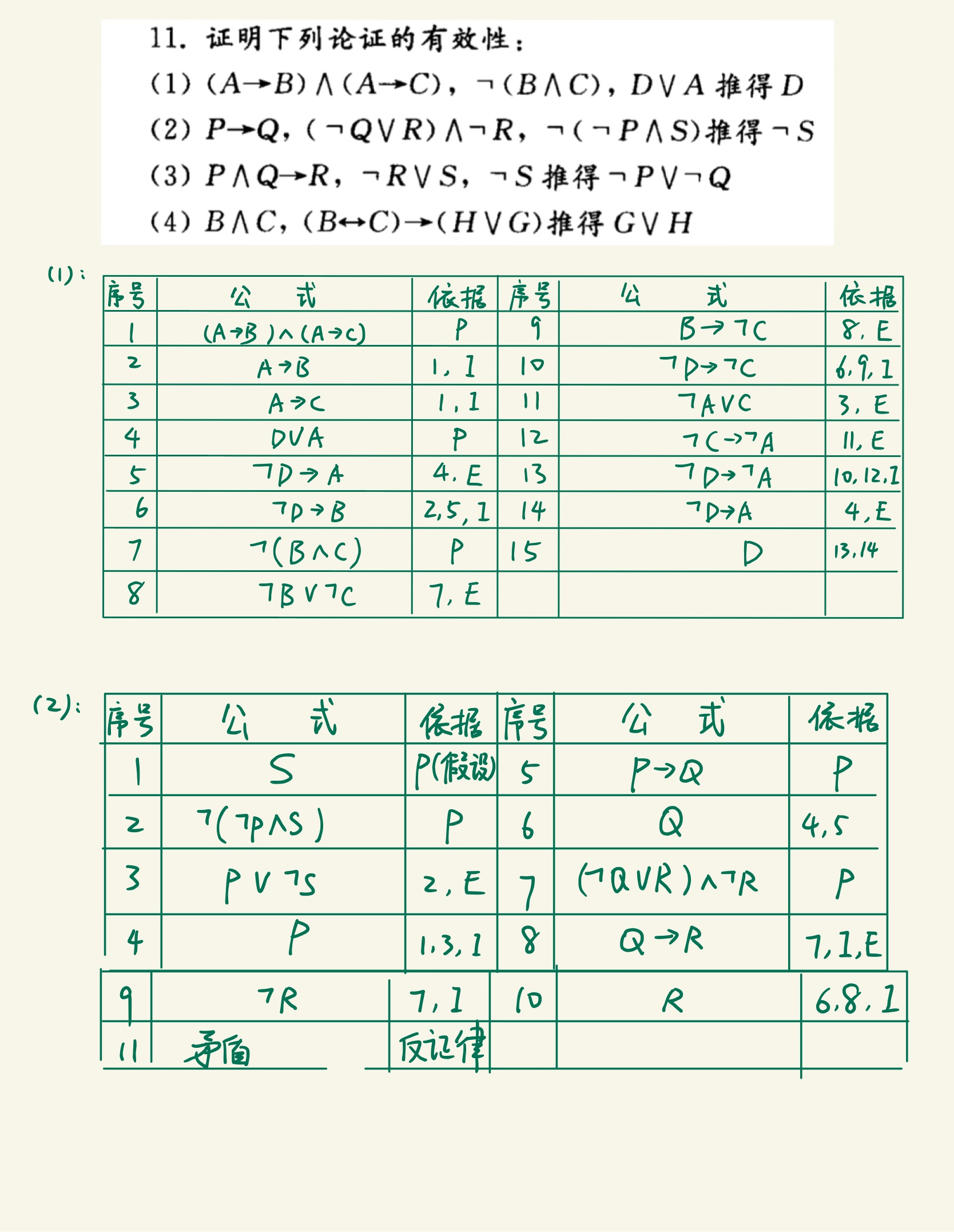
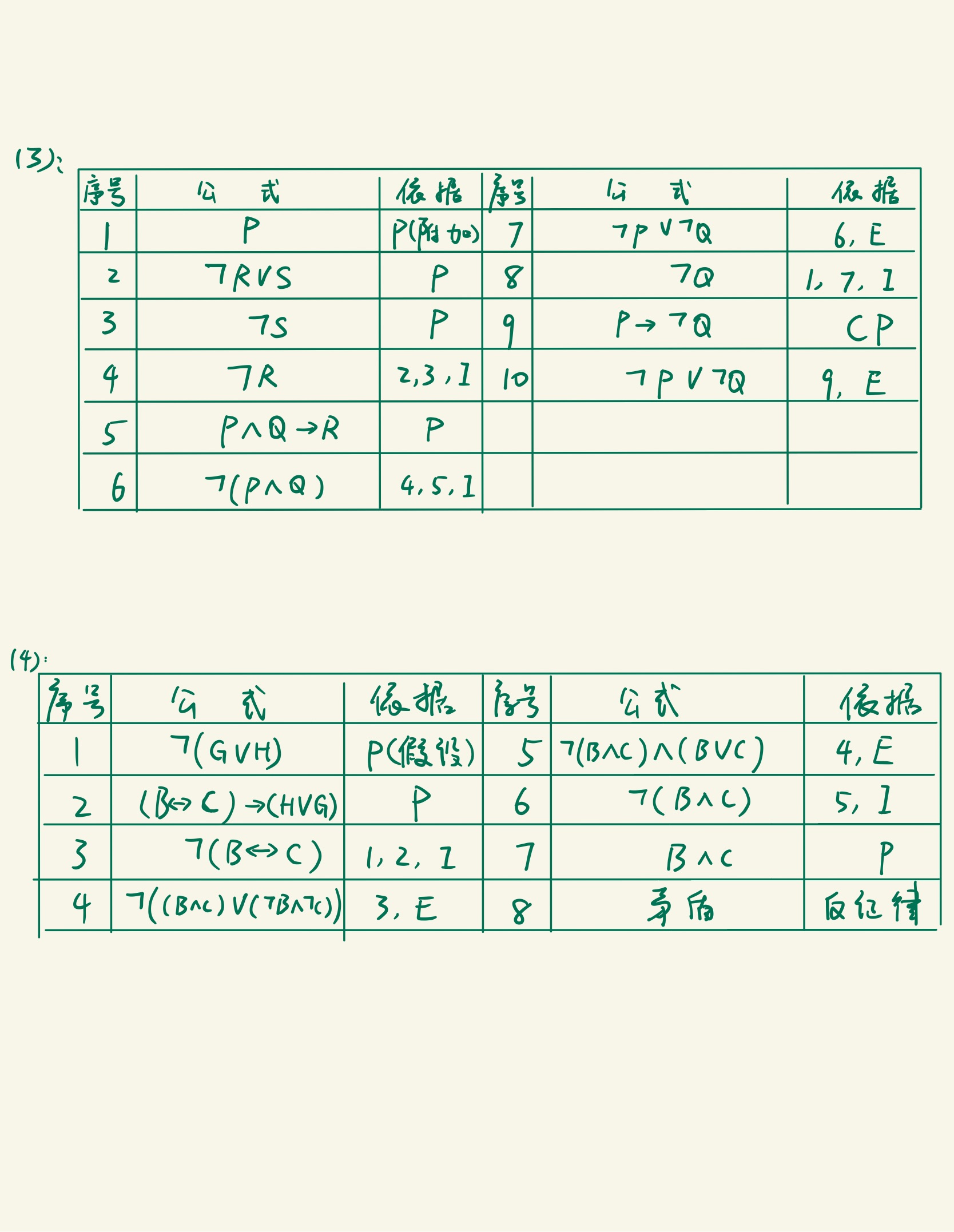
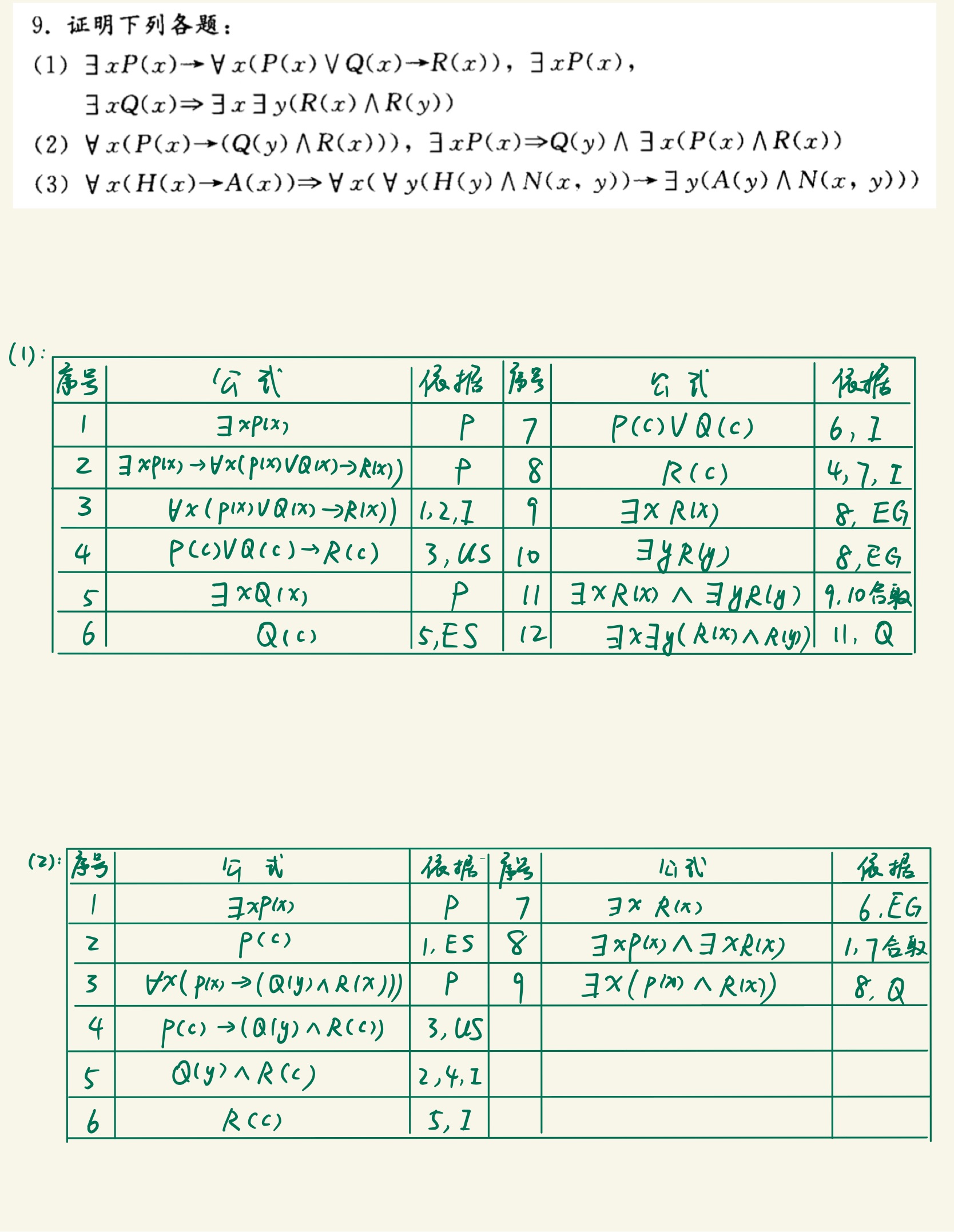
离散作业 1
离散作业 2
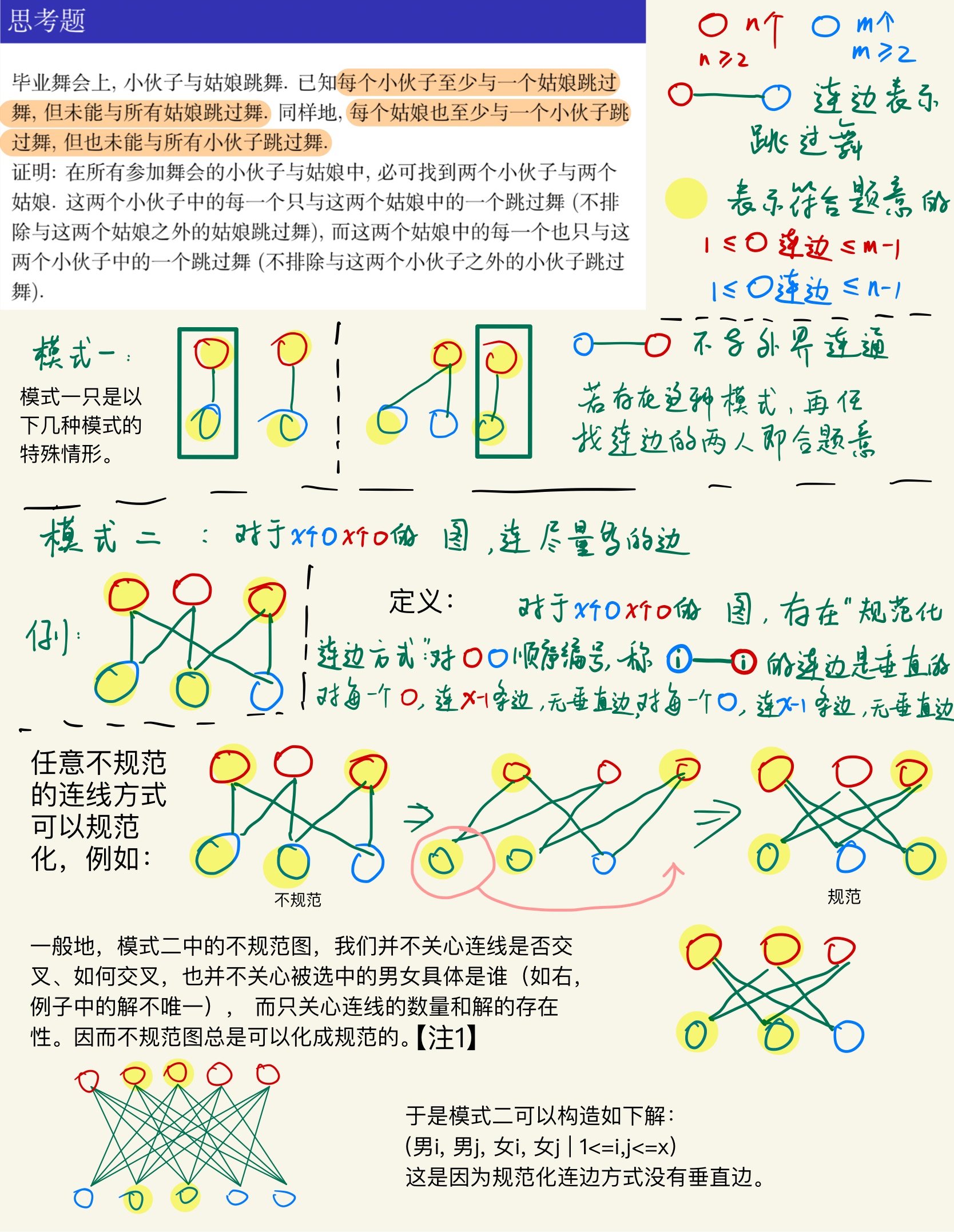
思考题
Pure love but limited.
博主的分析思路:(有点民科的感觉有木有OvO)
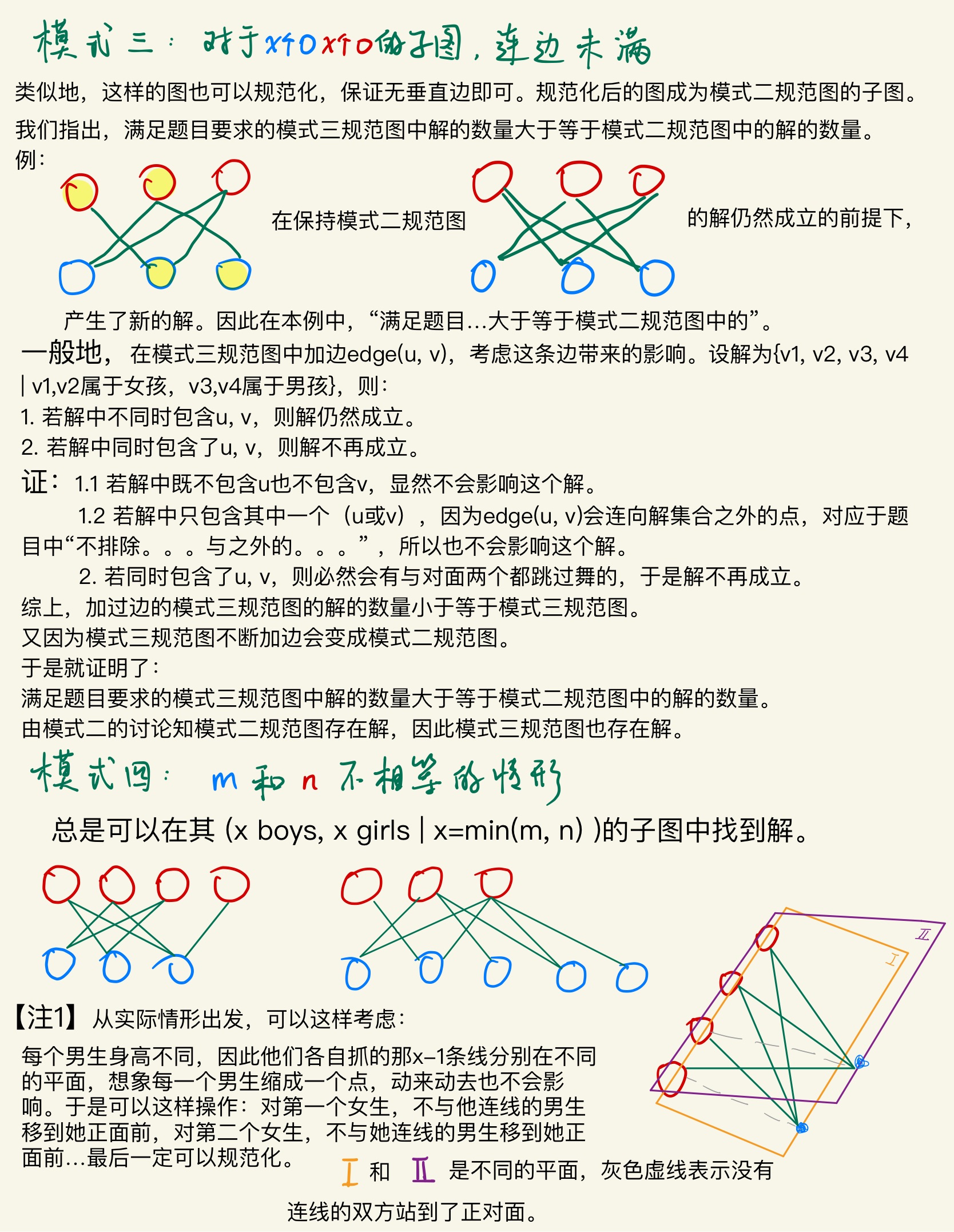
上面这种思路或许可以给出构造解。
注意:证明有误。在修了,目前有点思路。
老师的解答:
设有 $m$ 个小伙 $b_1,b_2,\cdots ,b_m$ ,有 $n$ 个姑娘 $g_1,g_2,\cdots ,g_n$. 设和第 $i$ 个小伙 $b_i$ 跳过舞的姑娘的集合为 $G_i$ ,其中 $i=1,2,\cdots ,m$.
对 $G_1,G_2,\cdots ,G_m$ 有两种情况:
$\mathcal{A}:$
存在 $1\leqslant i<j\leqslant m$ ,使得 $G_i\nsubseteq G_j$ 且 $G_j\nsubseteq G_i$ .
于是存在 $g_k\in G_i$ 但 $g_k\notin G_j$ ;存在 $g_l\in G_j$ 但 $g_l\notin G_i$ .
这样对于小伙 $b_i,b_j$ 和姑娘 $g_k,g_l$ 结论成立 .
$\mathcal{B}:$
对任意 $1\leqslant i<j\leqslant m$ ,要么 $G_i\subseteq G_j$ ,要么 $G_j\subseteq G_i$ .
于是可以按照 $\subseteq$ 排序:
这与题设矛盾。
综上,结论得证。
离散作业 3
离散作业 4
离散作业 5
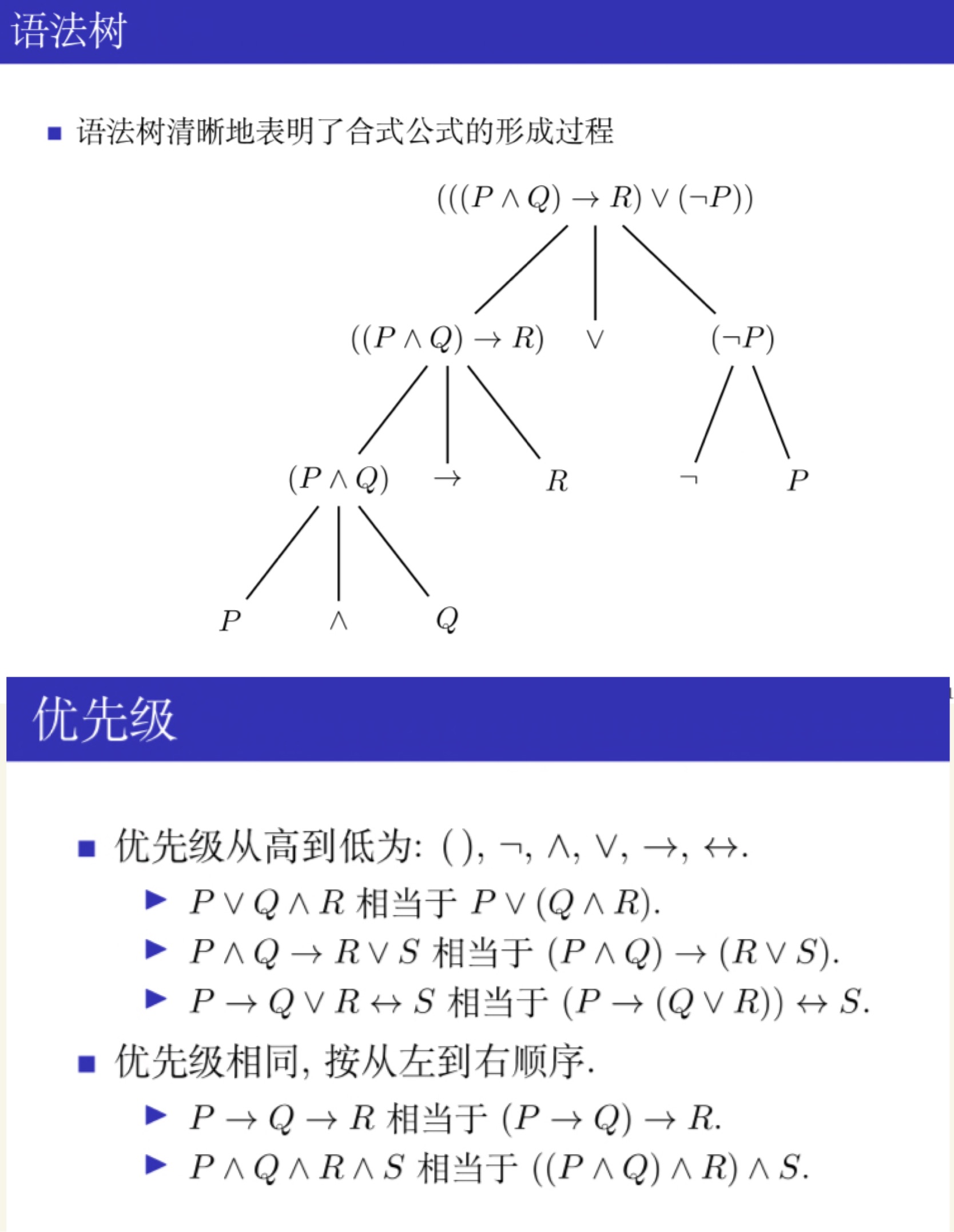
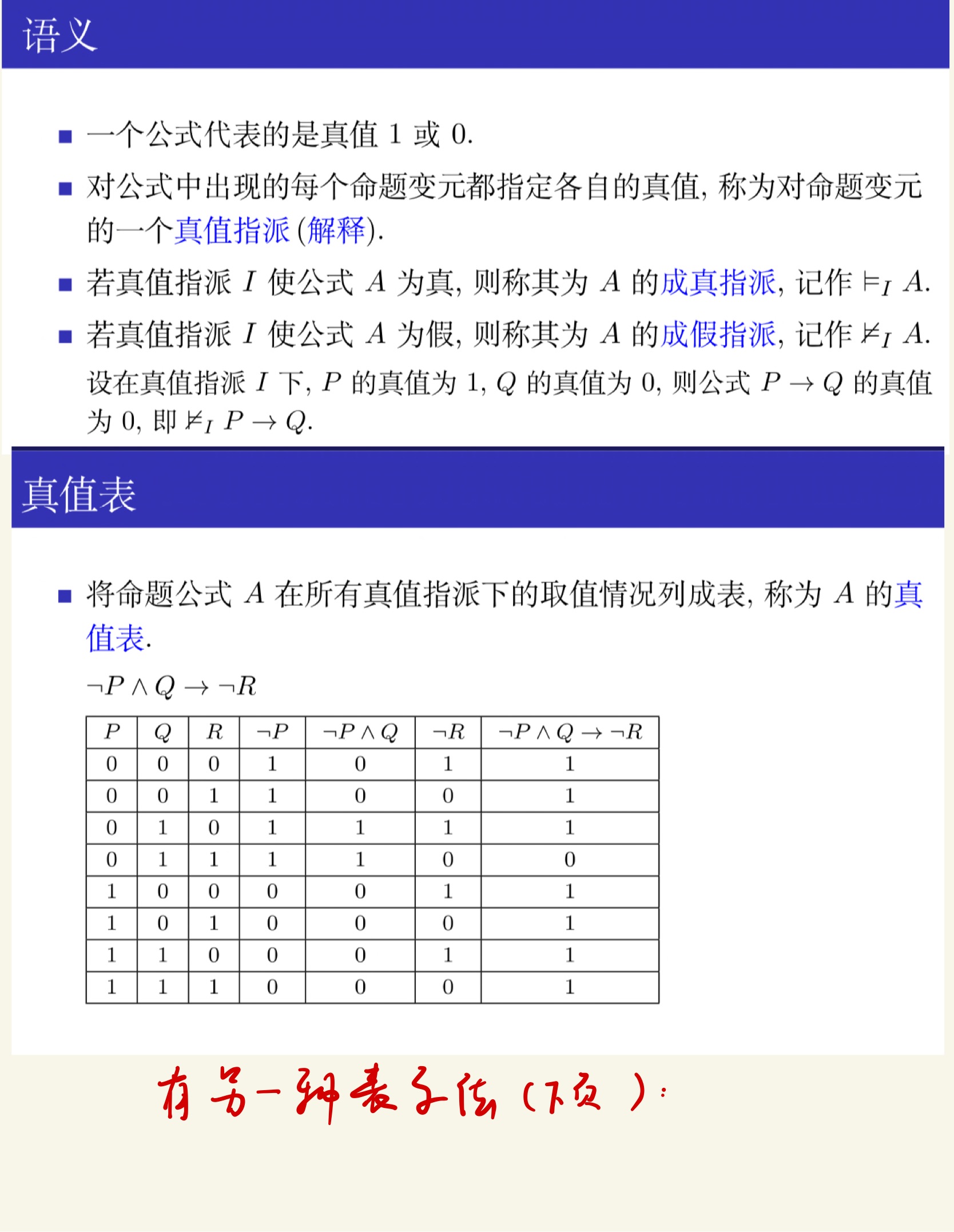
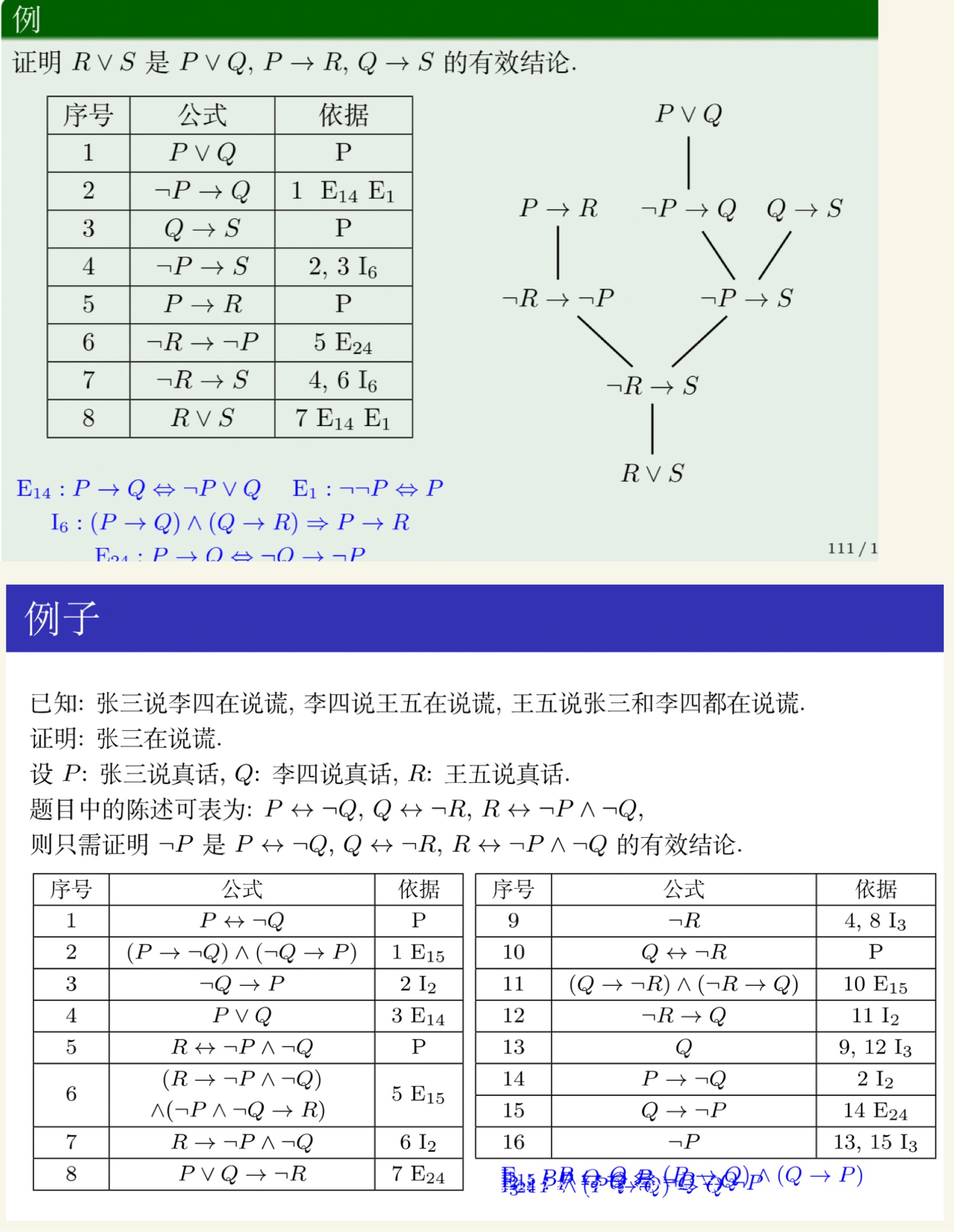
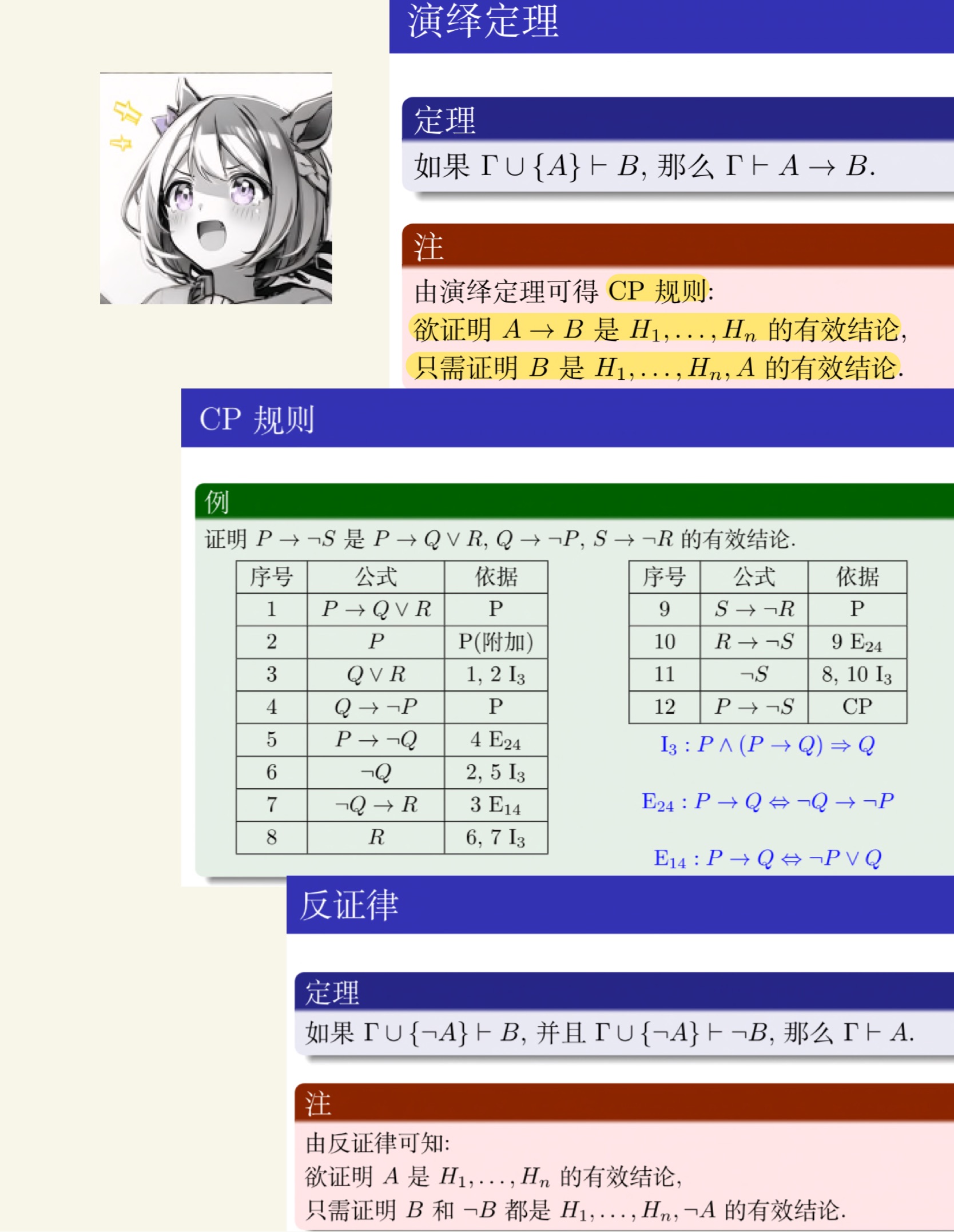
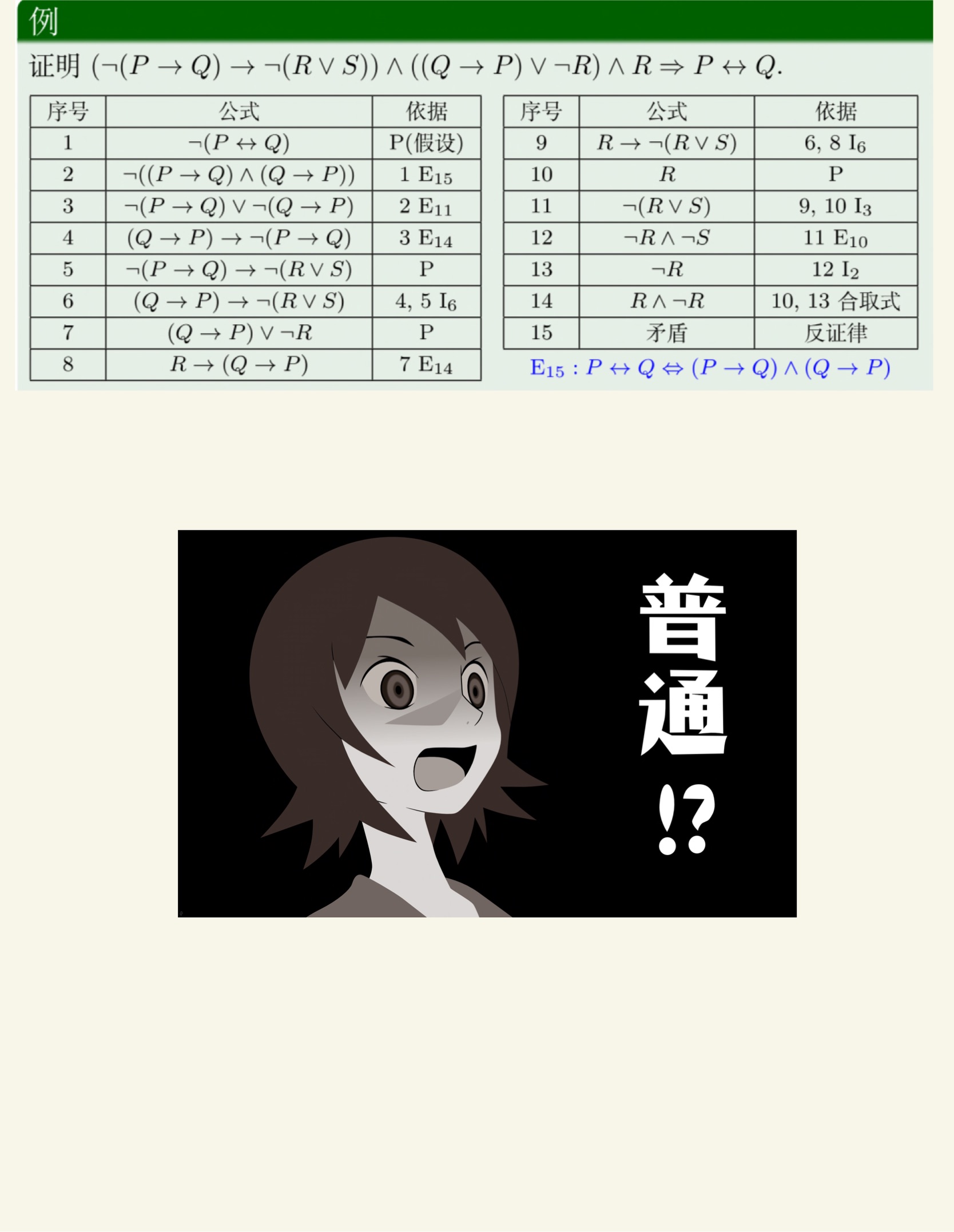
命题逻辑
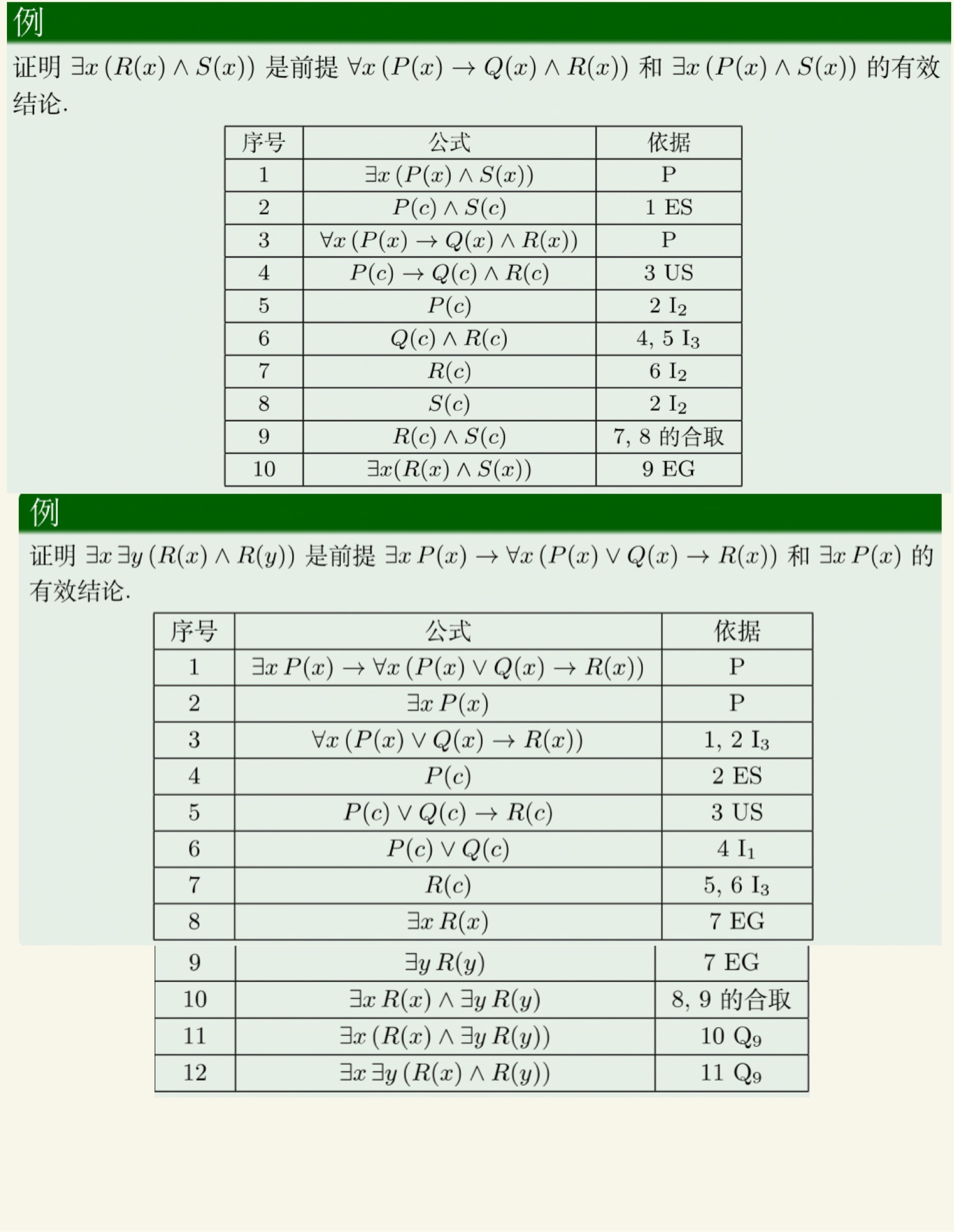
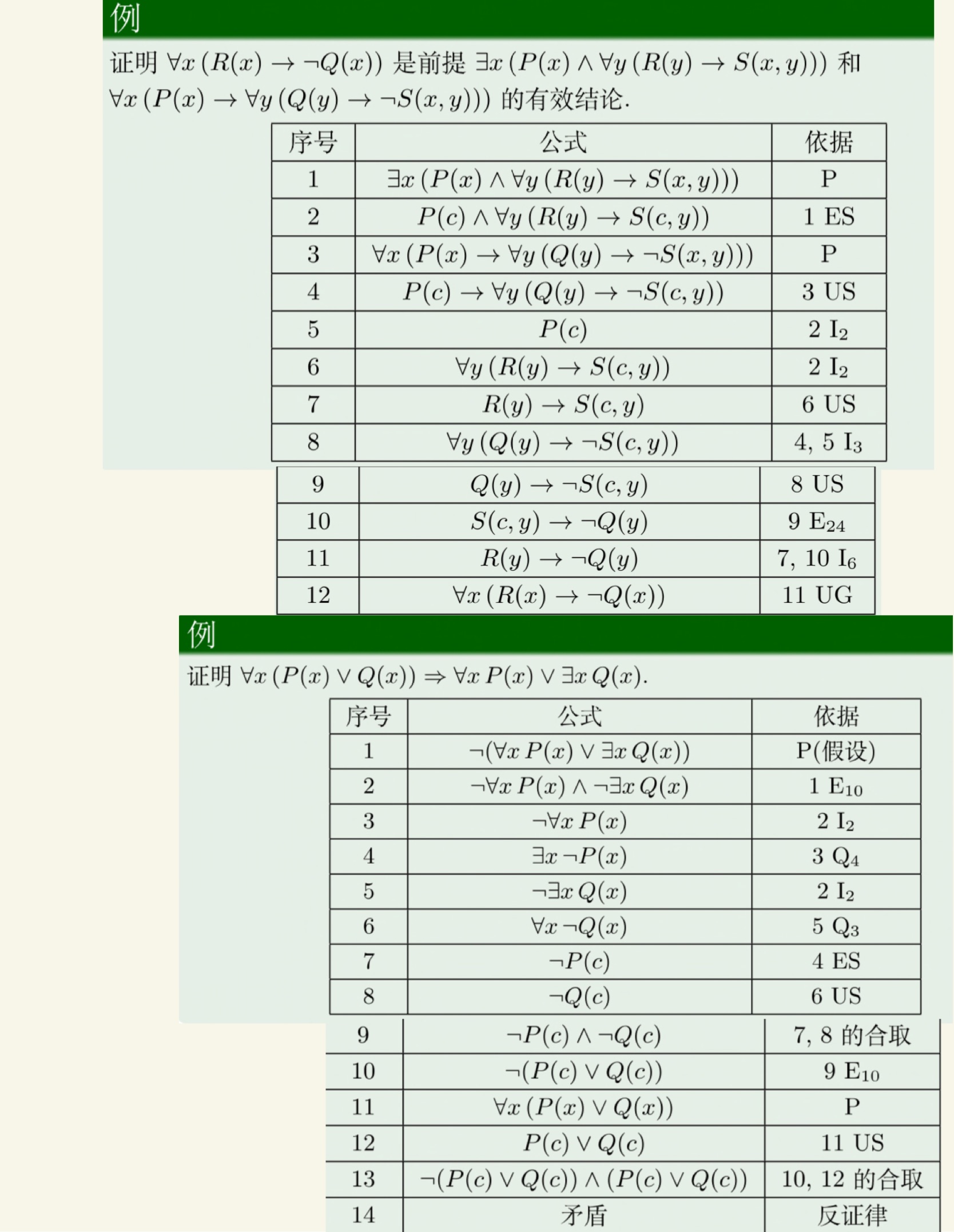
谓词逻辑
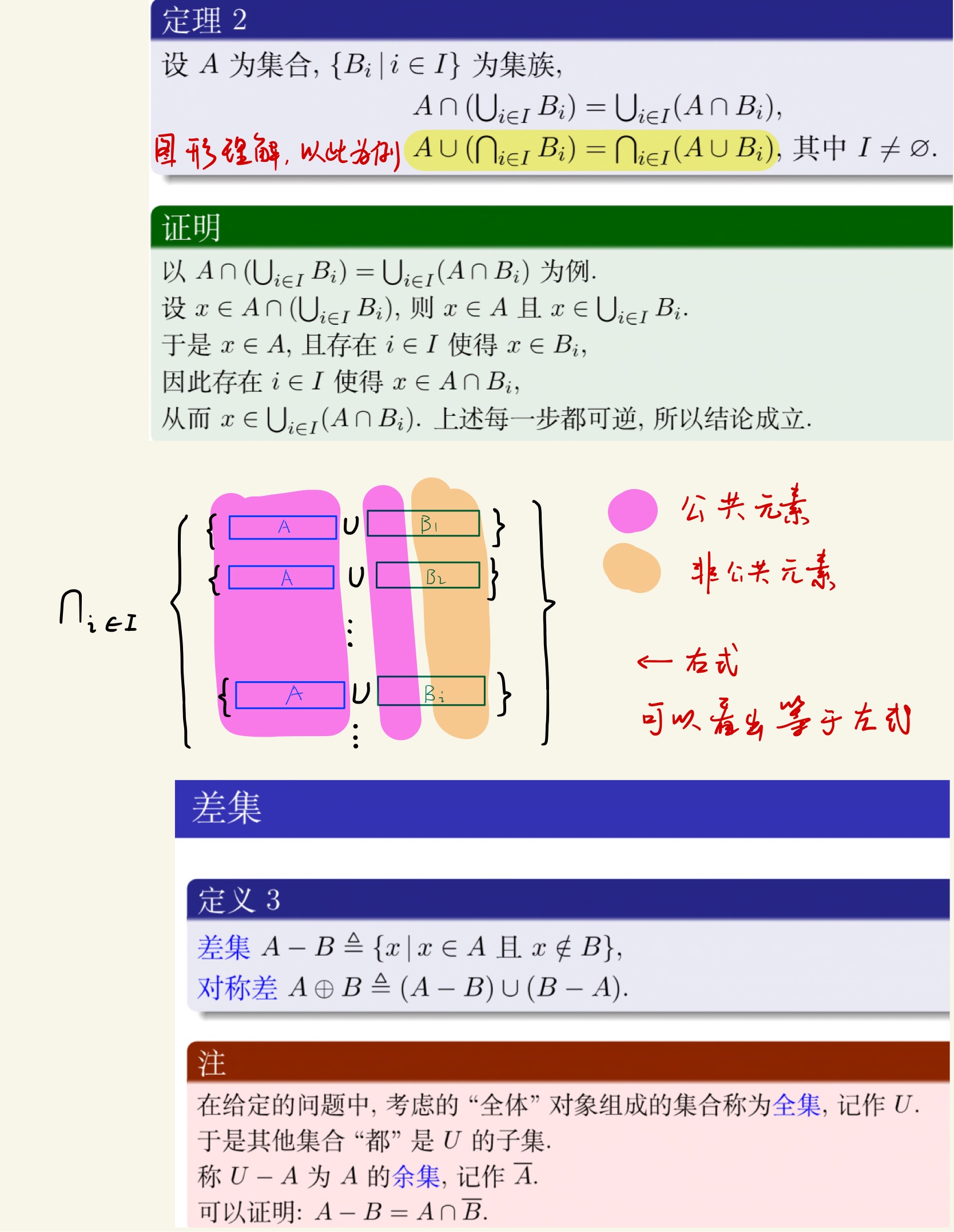
集合
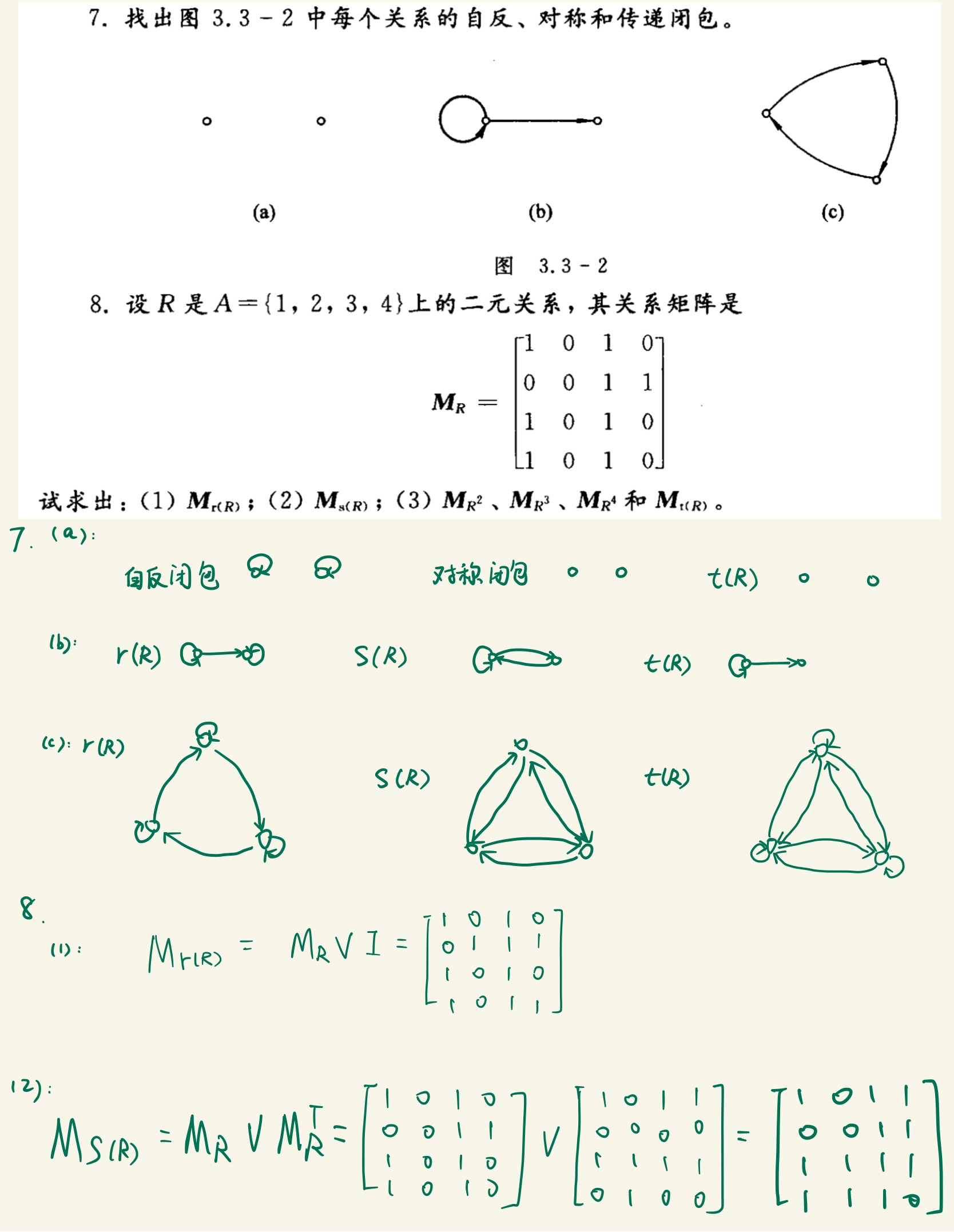
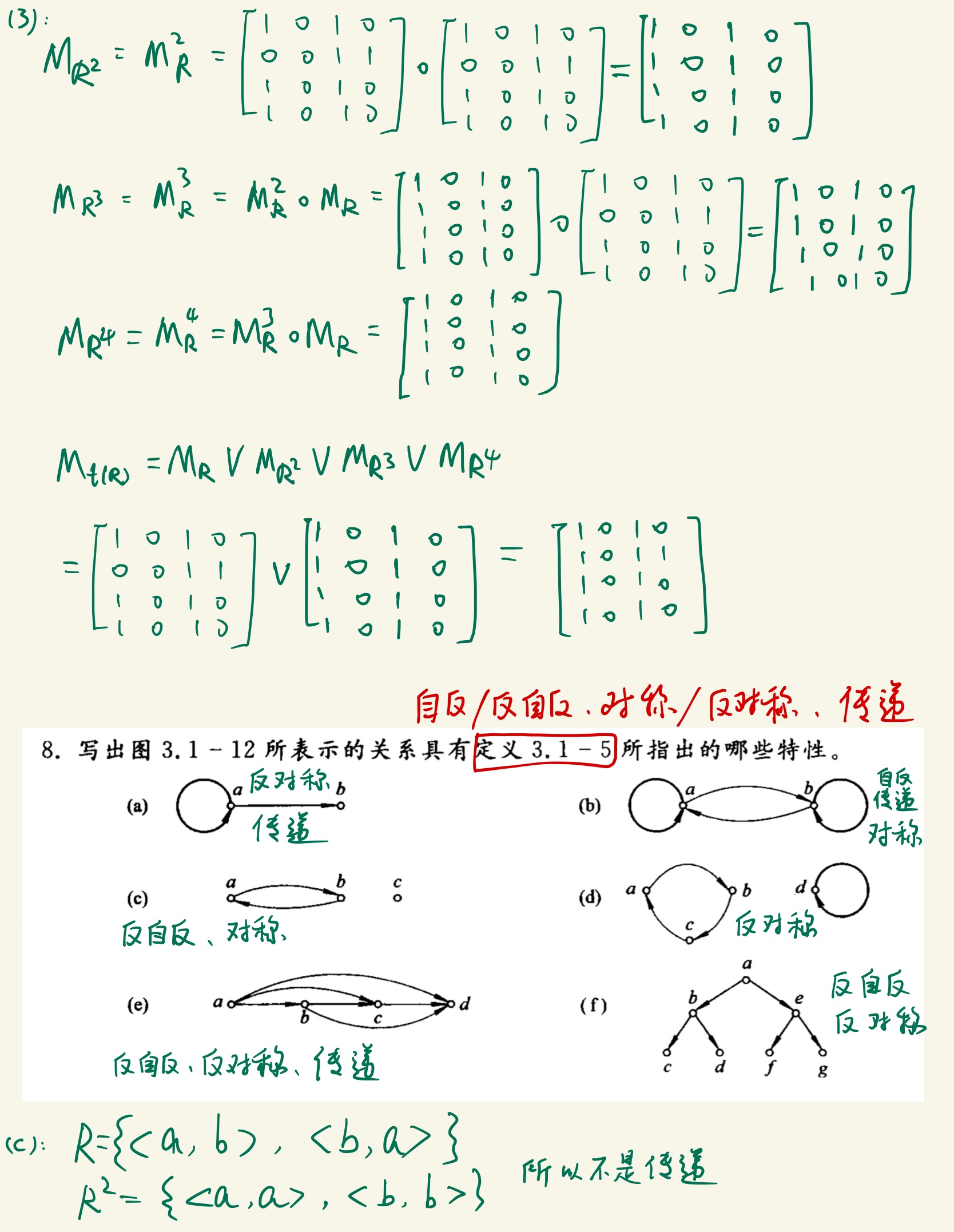
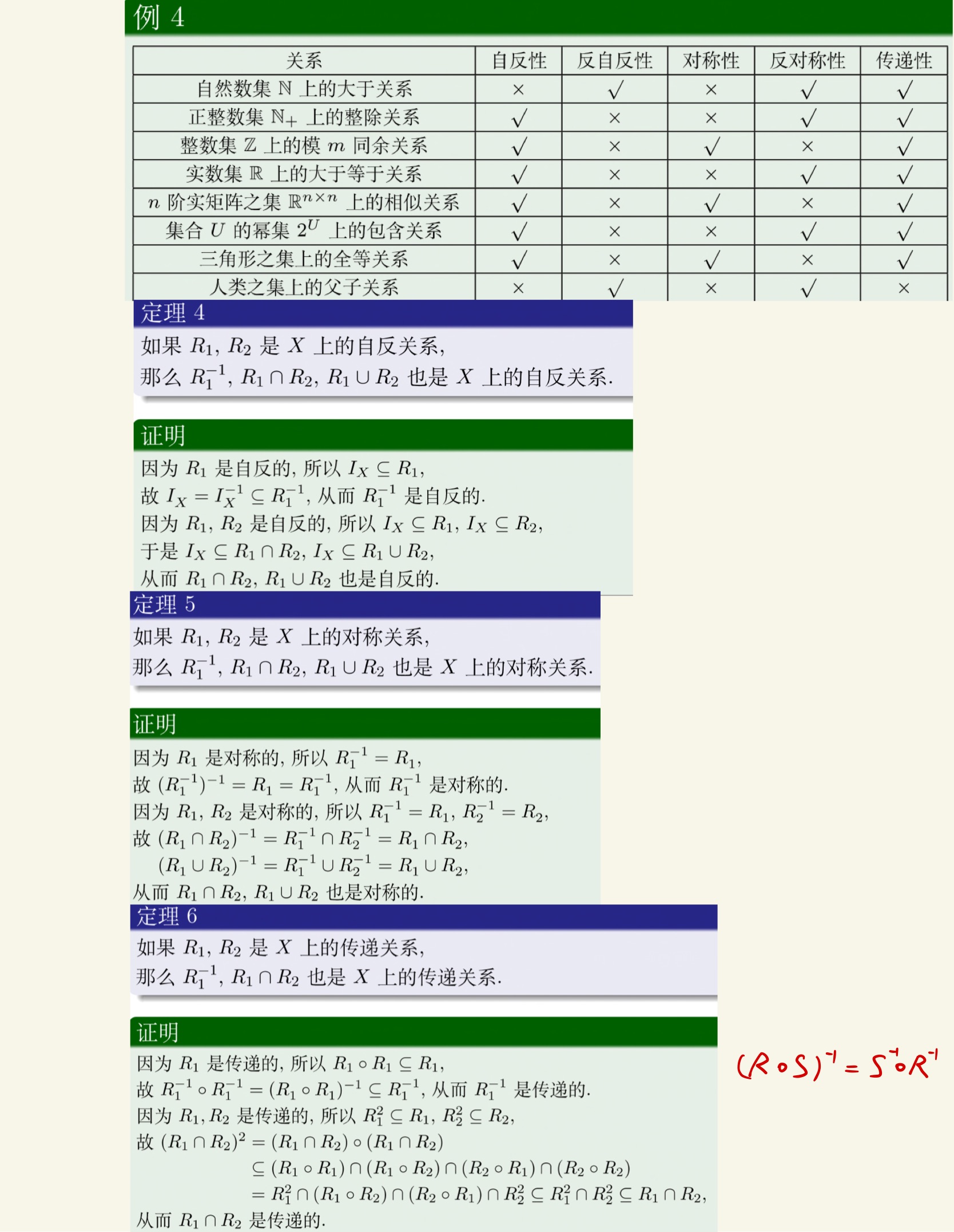
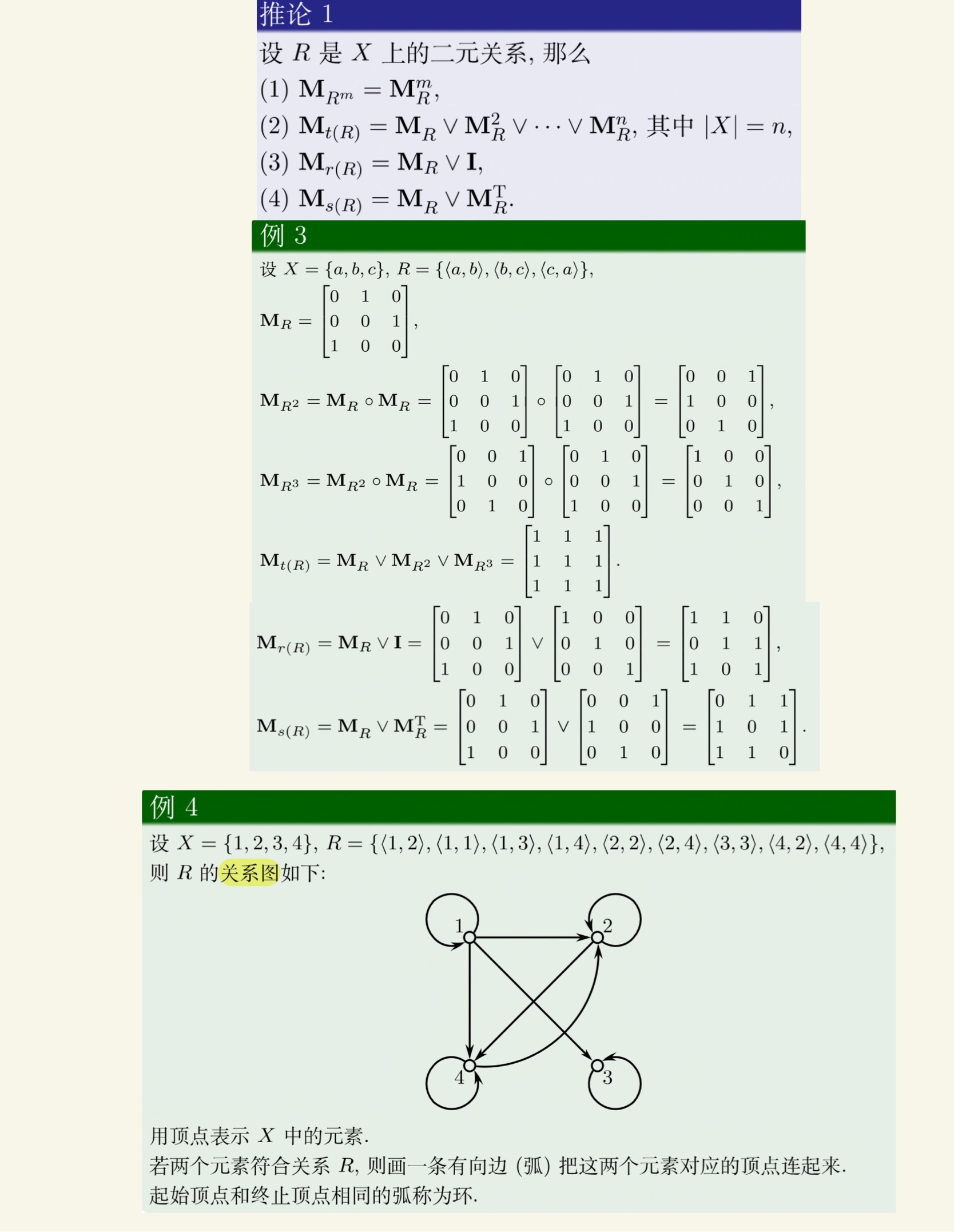
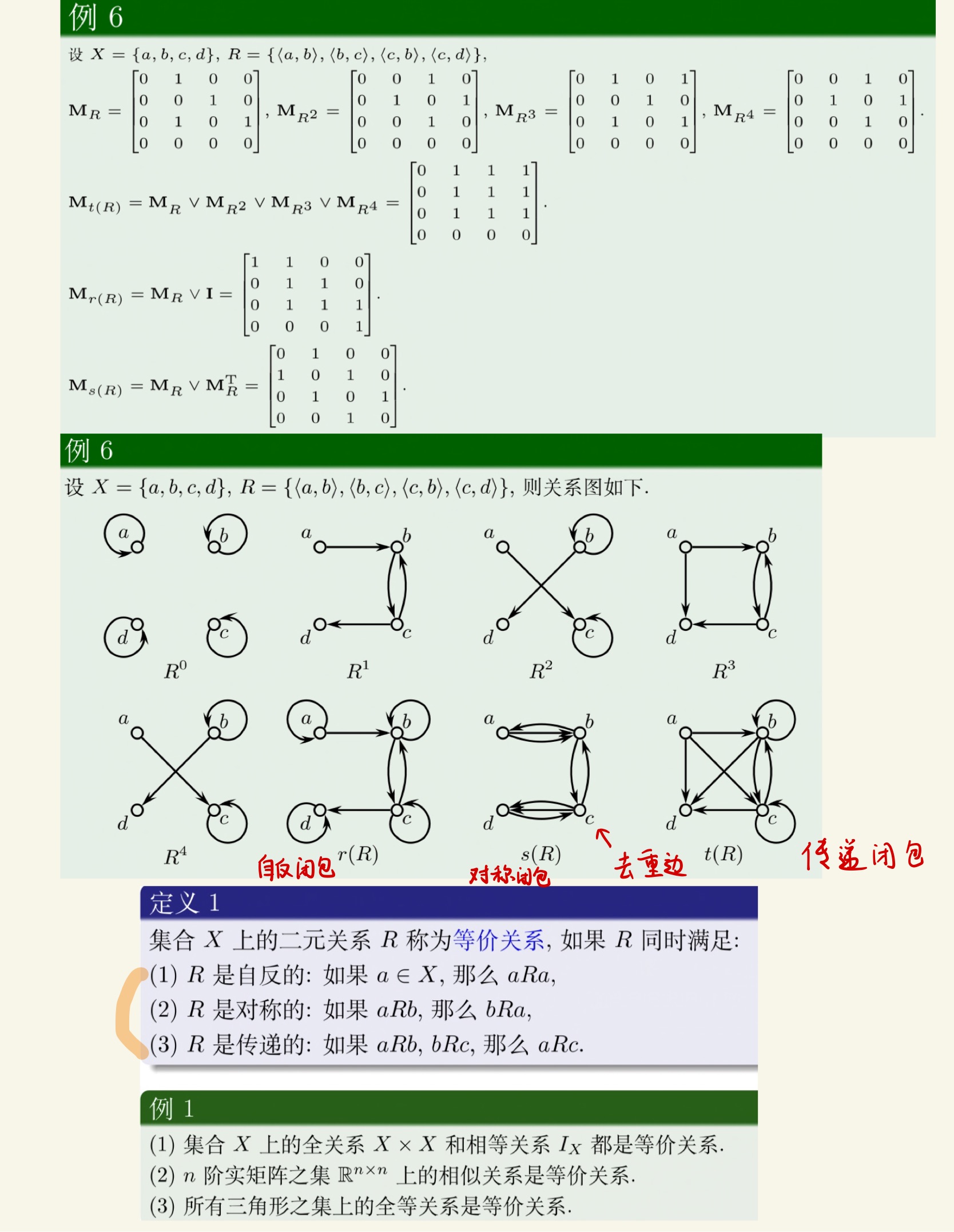
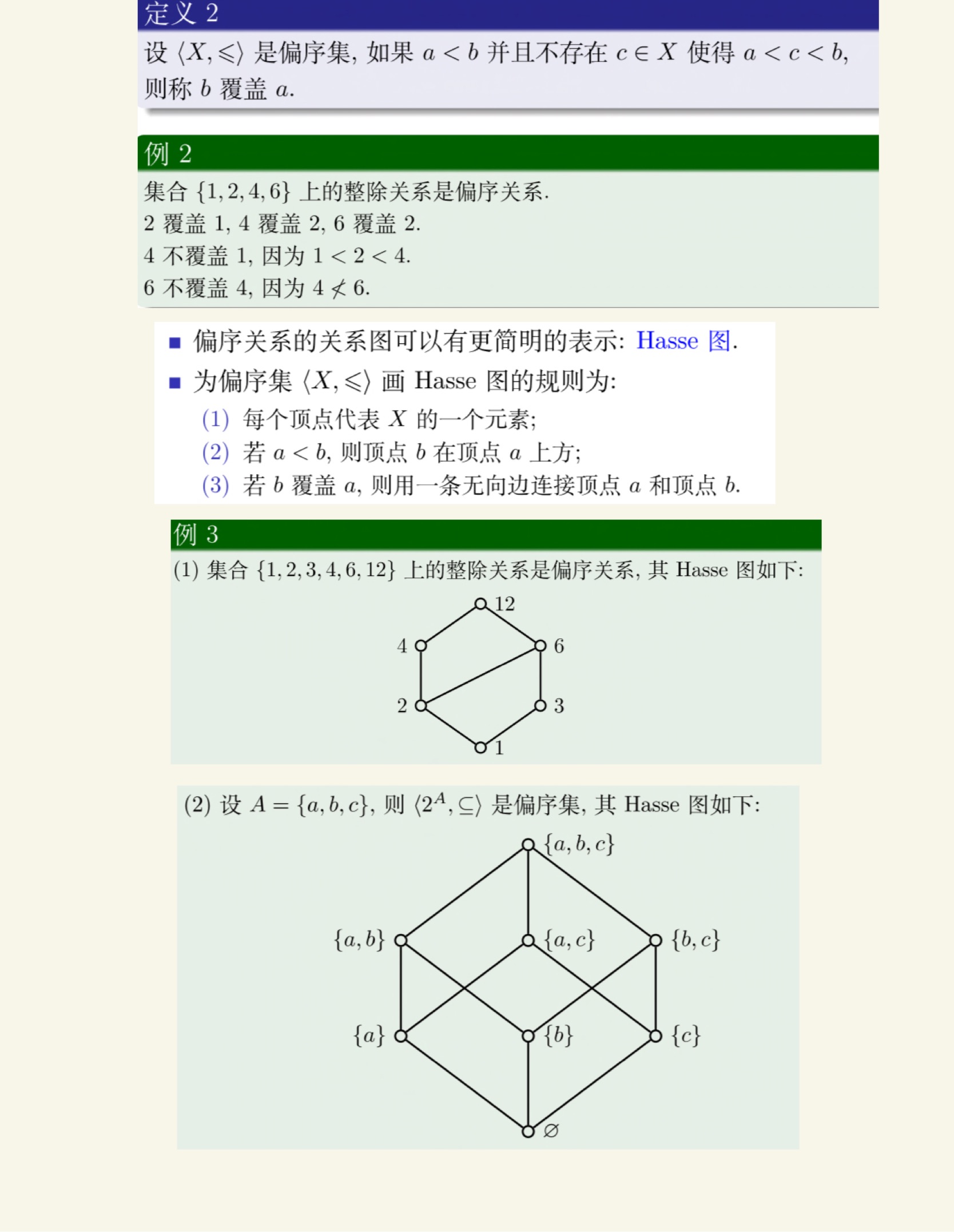
关系
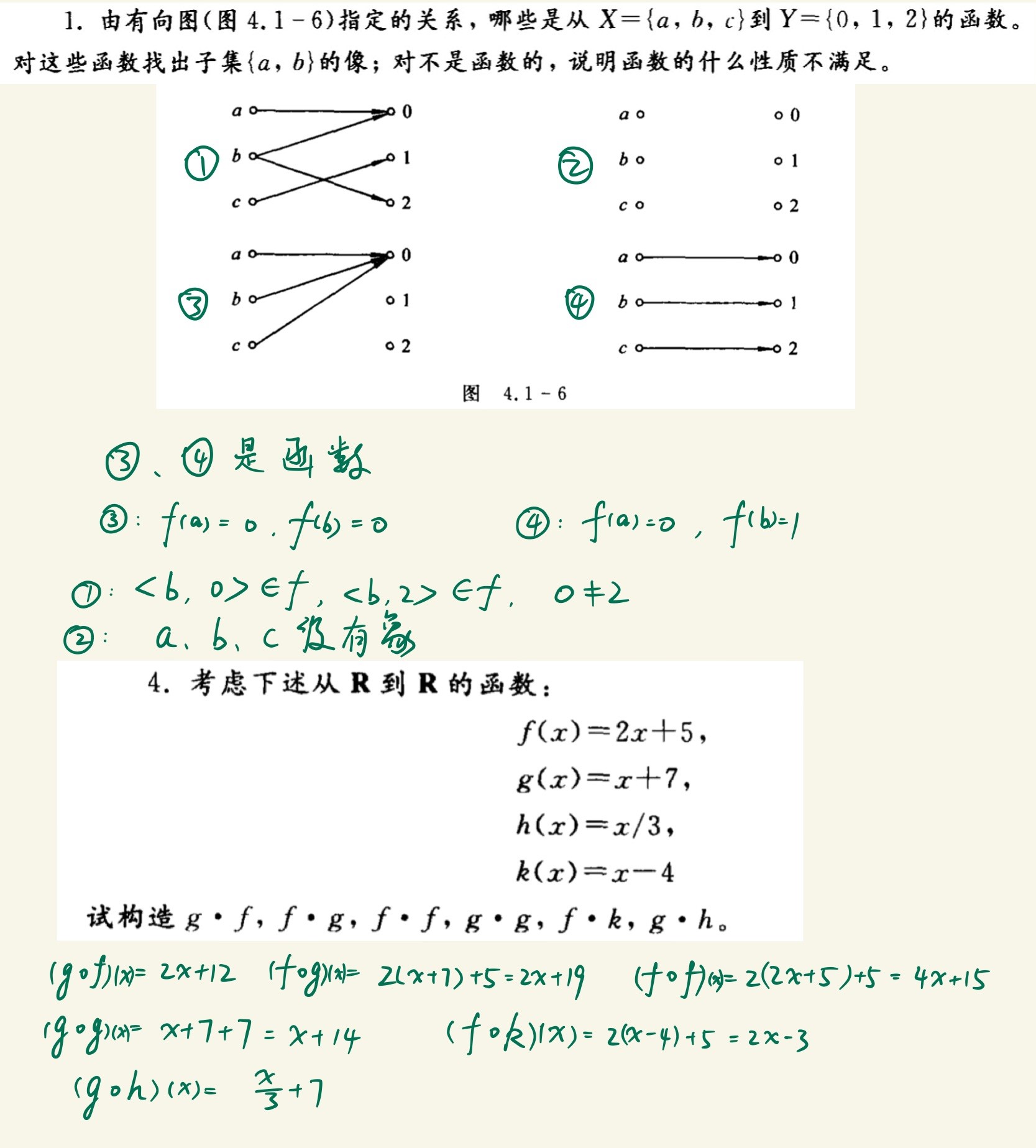
映射
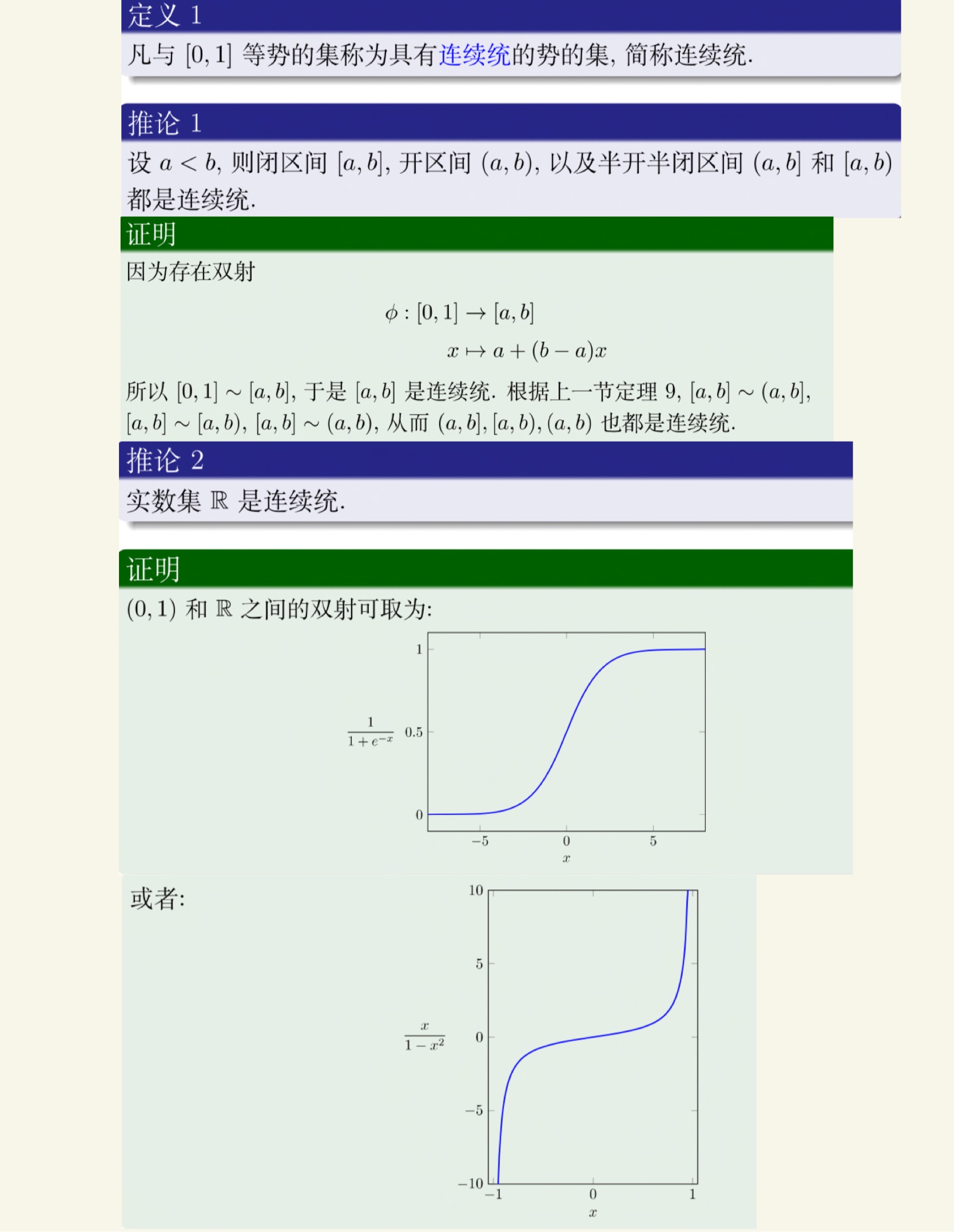
无穷集合
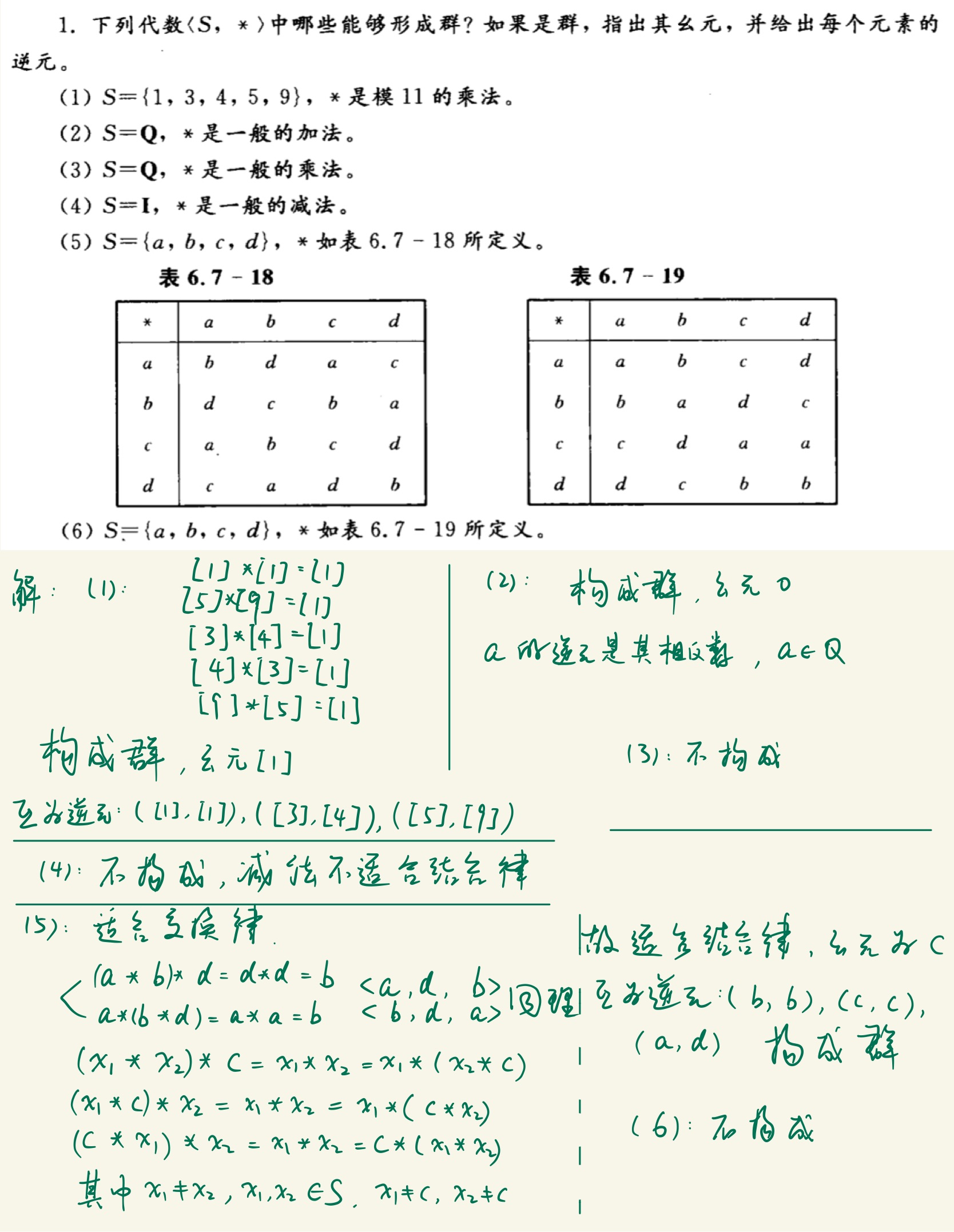
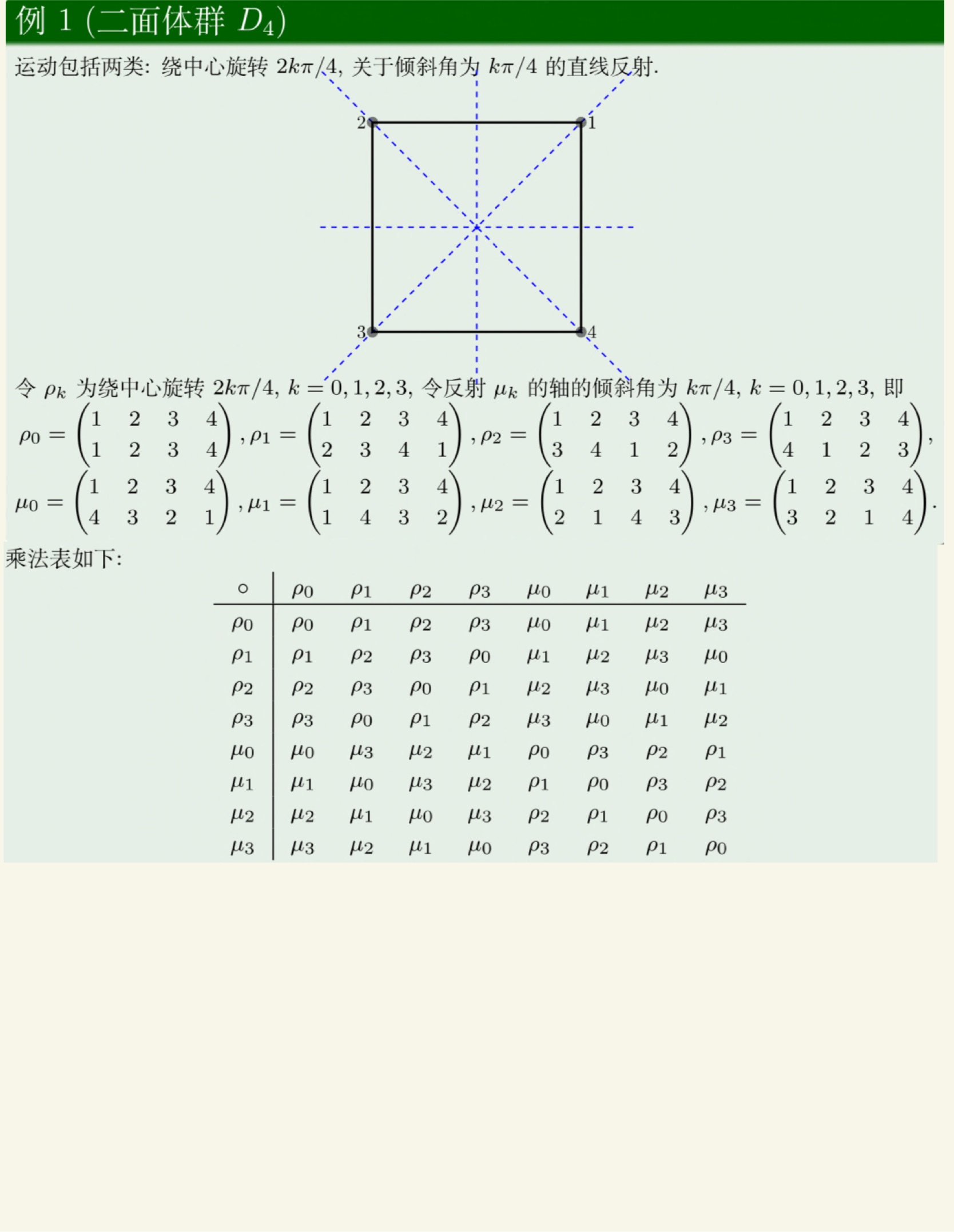
抽象代数
这部分是最难理解的,在课堂上跟思路非常耗神。
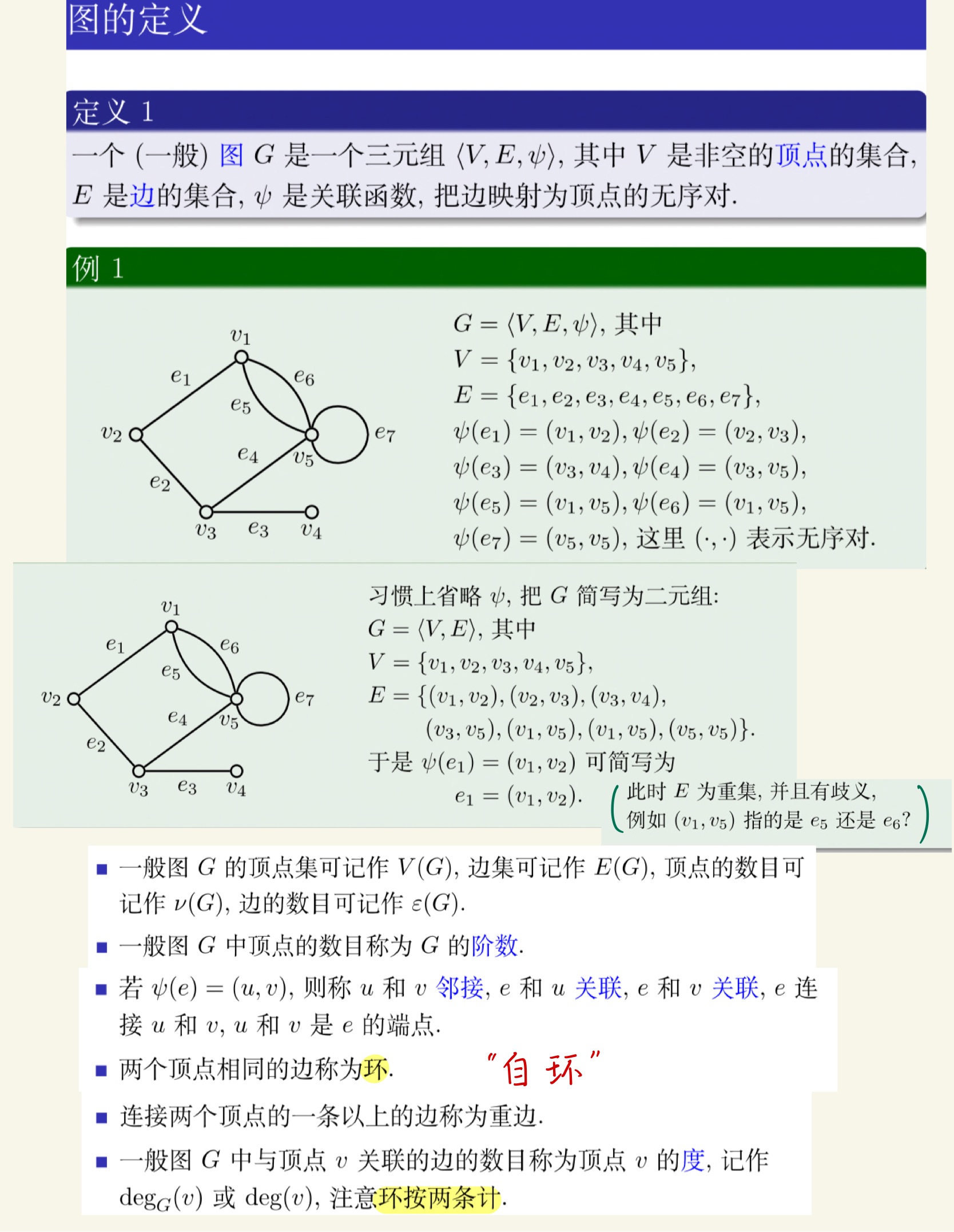
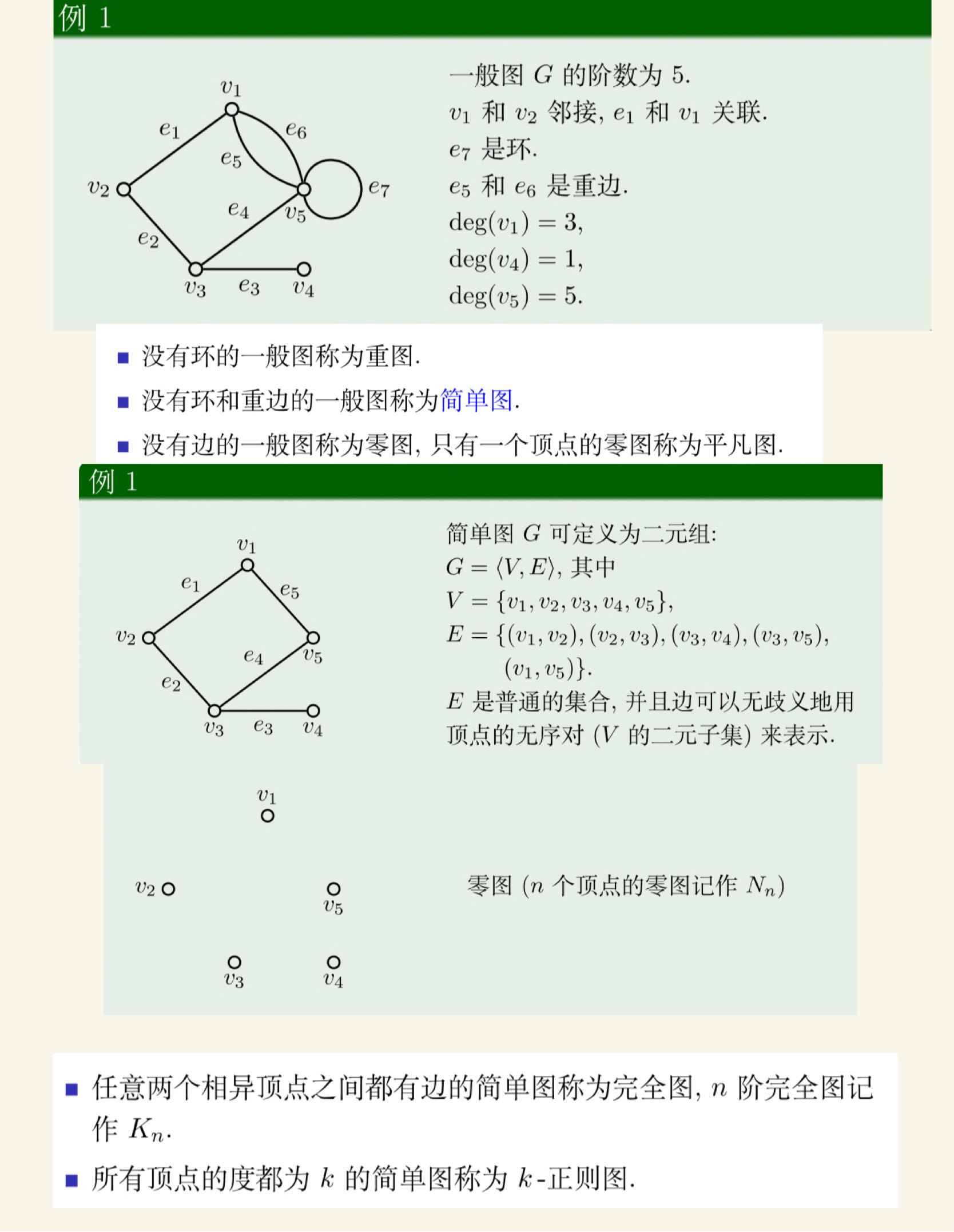
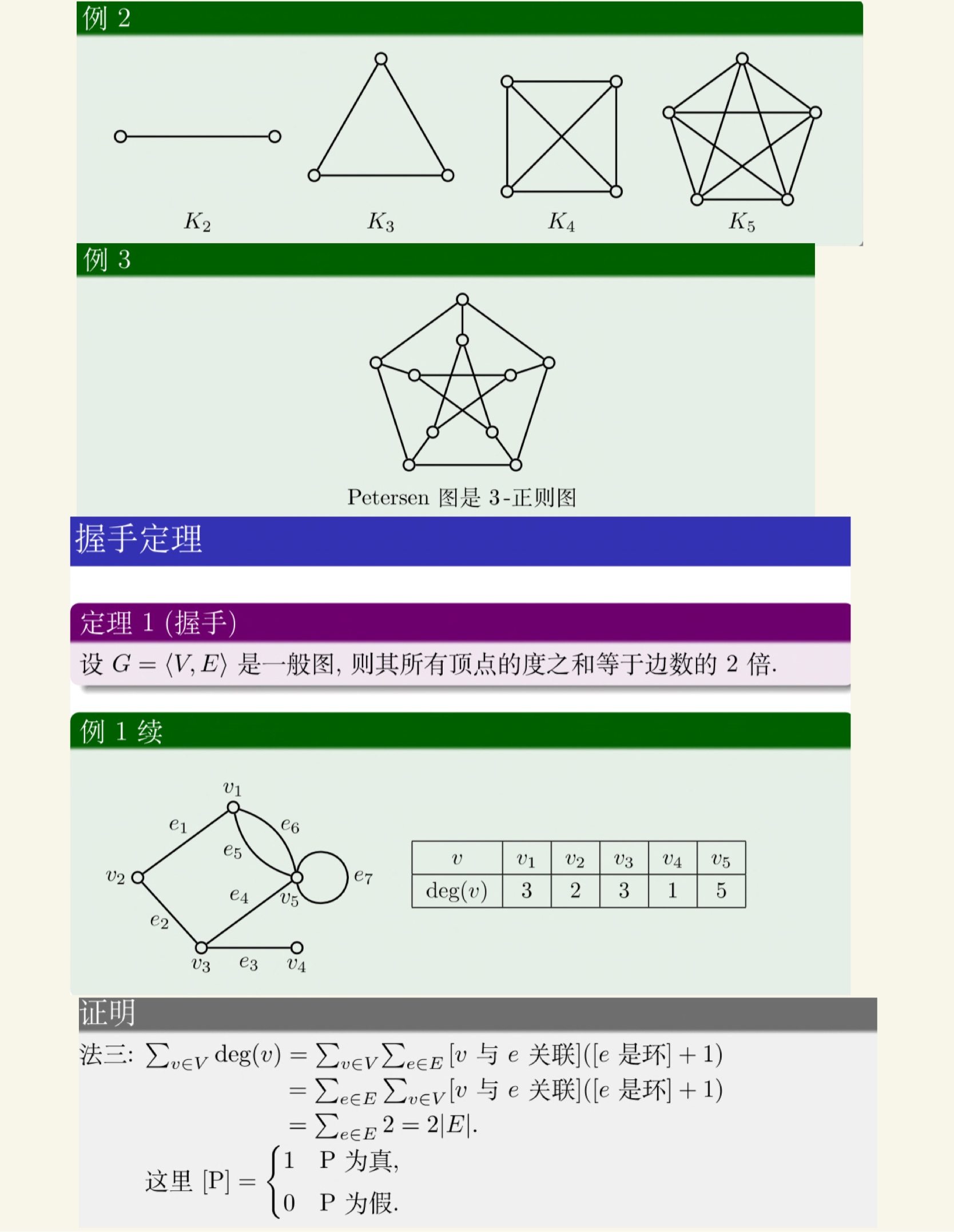
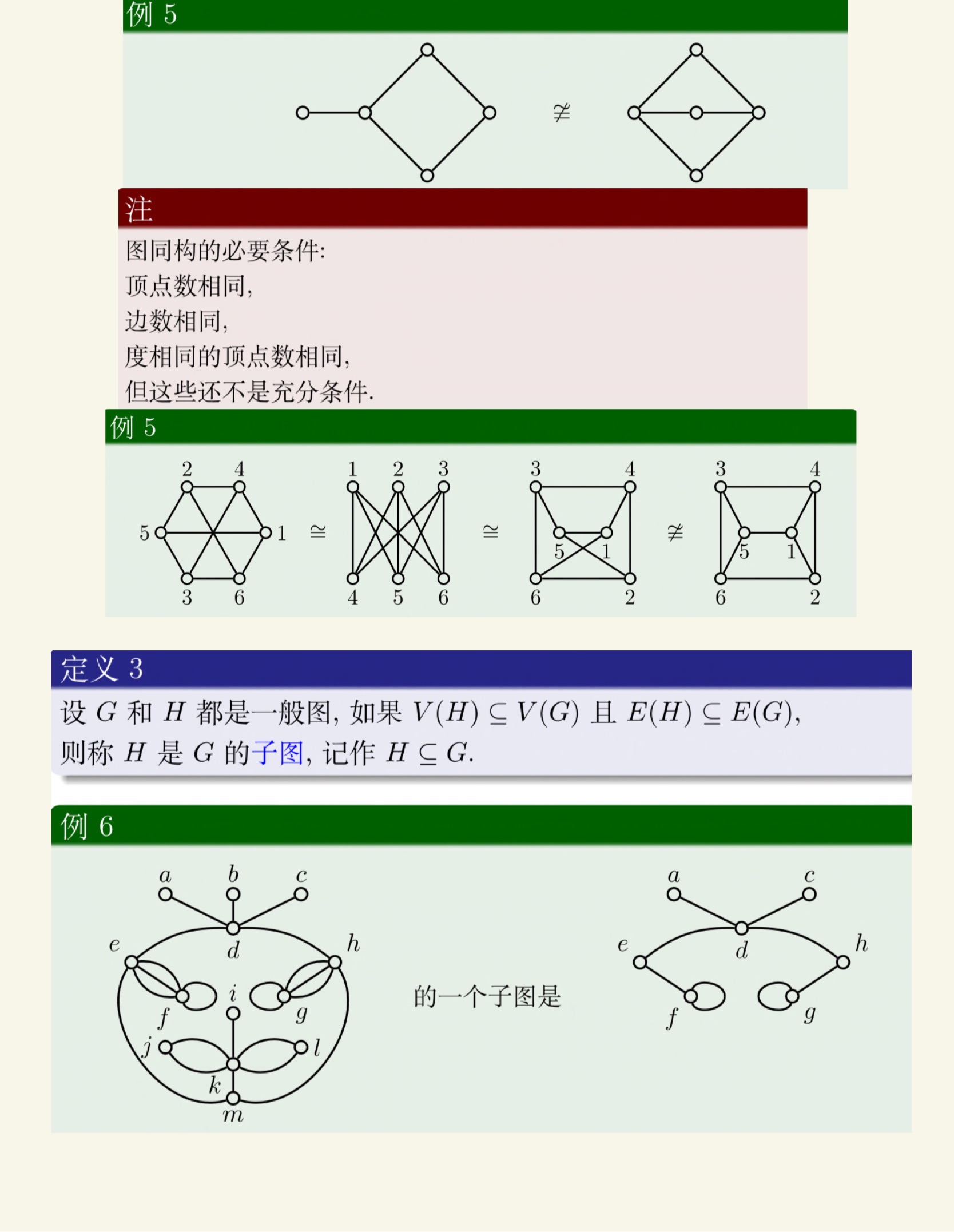
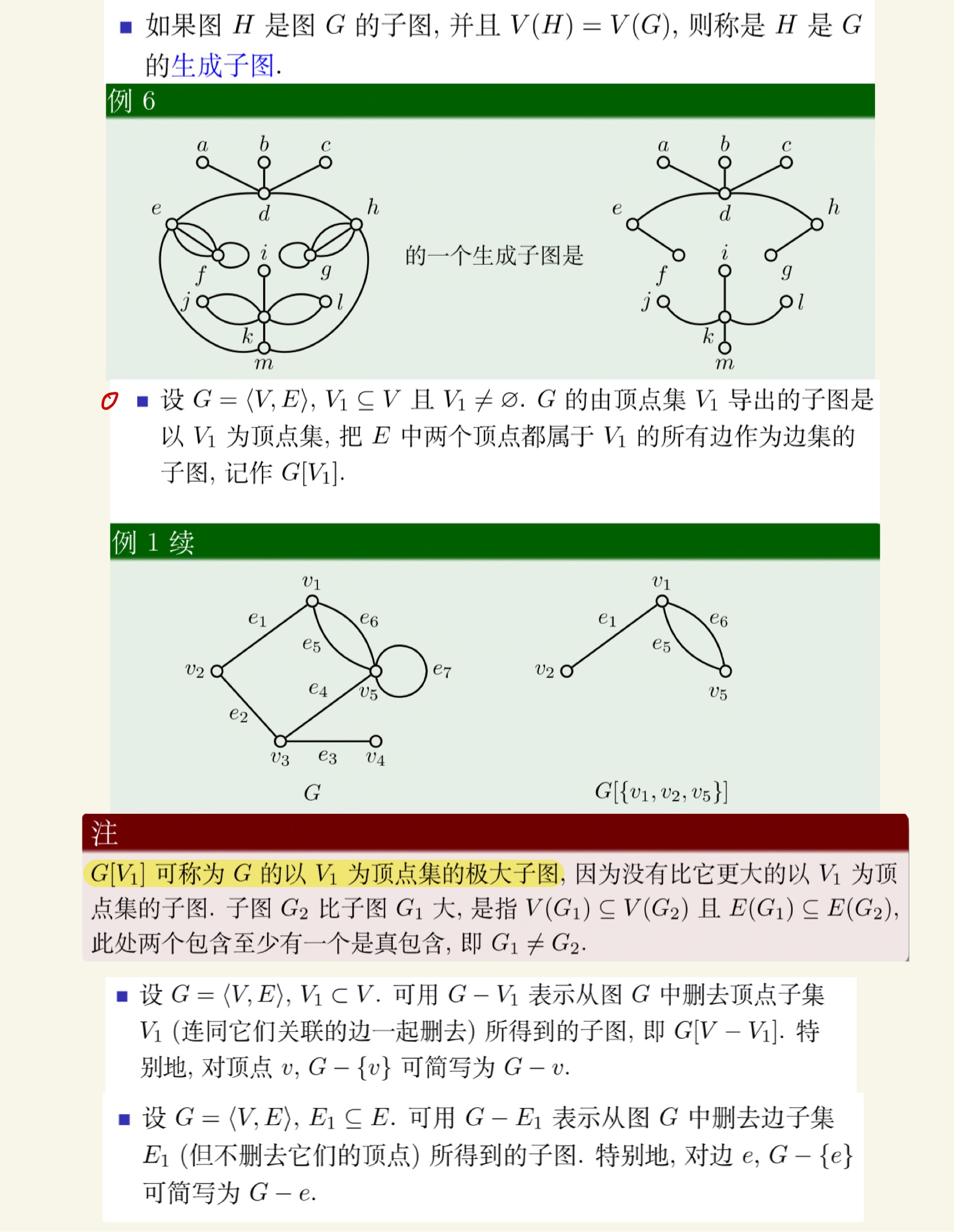
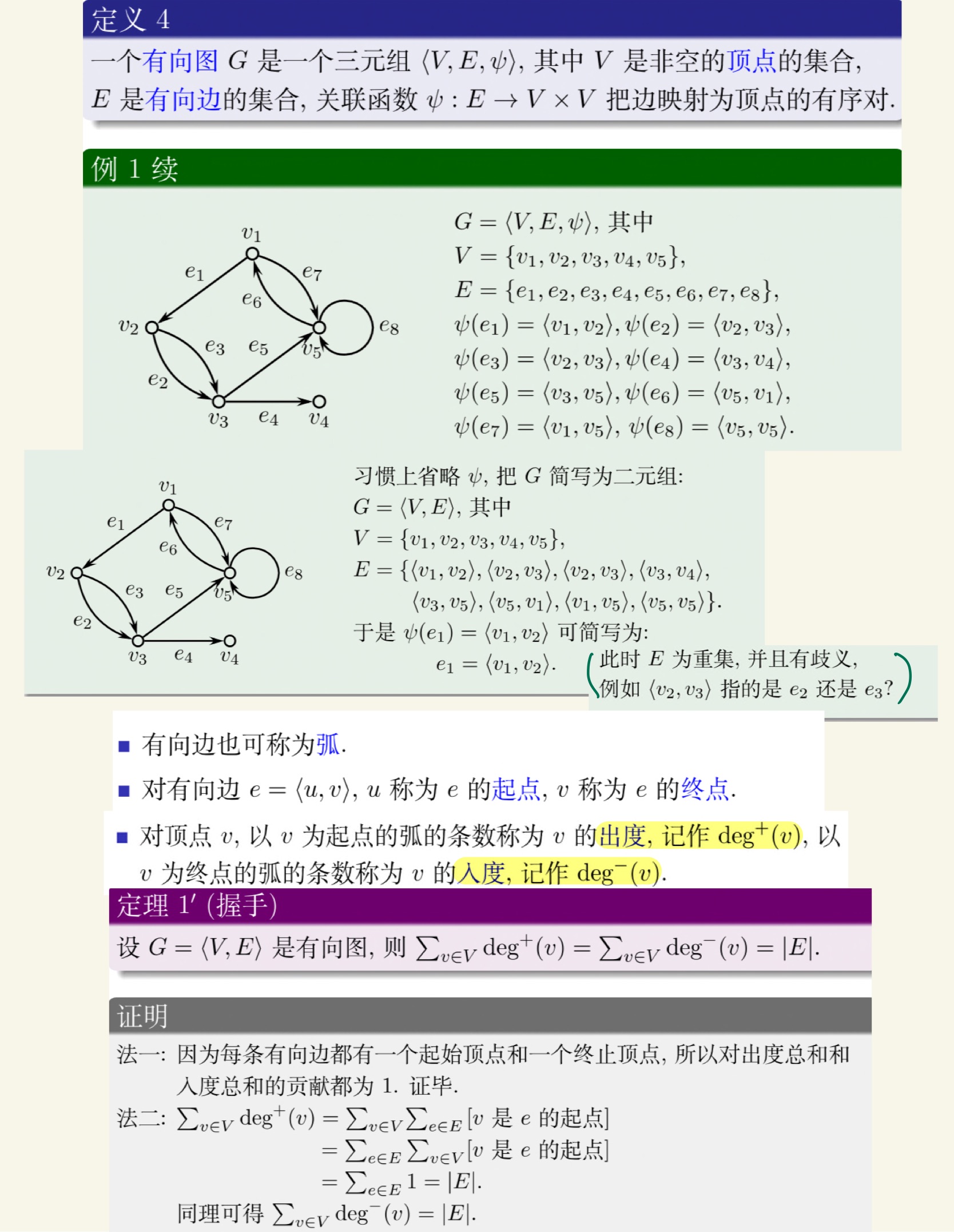
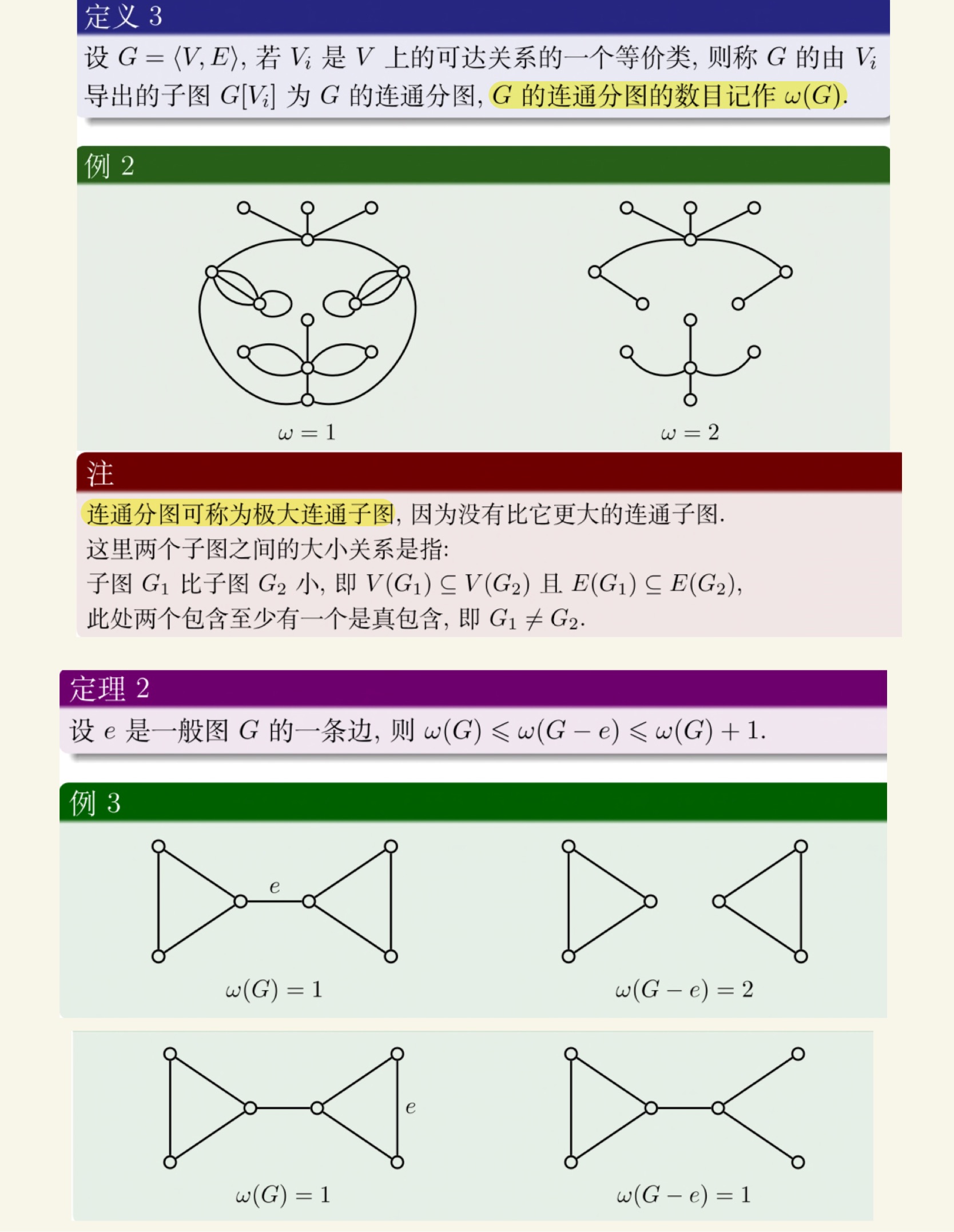
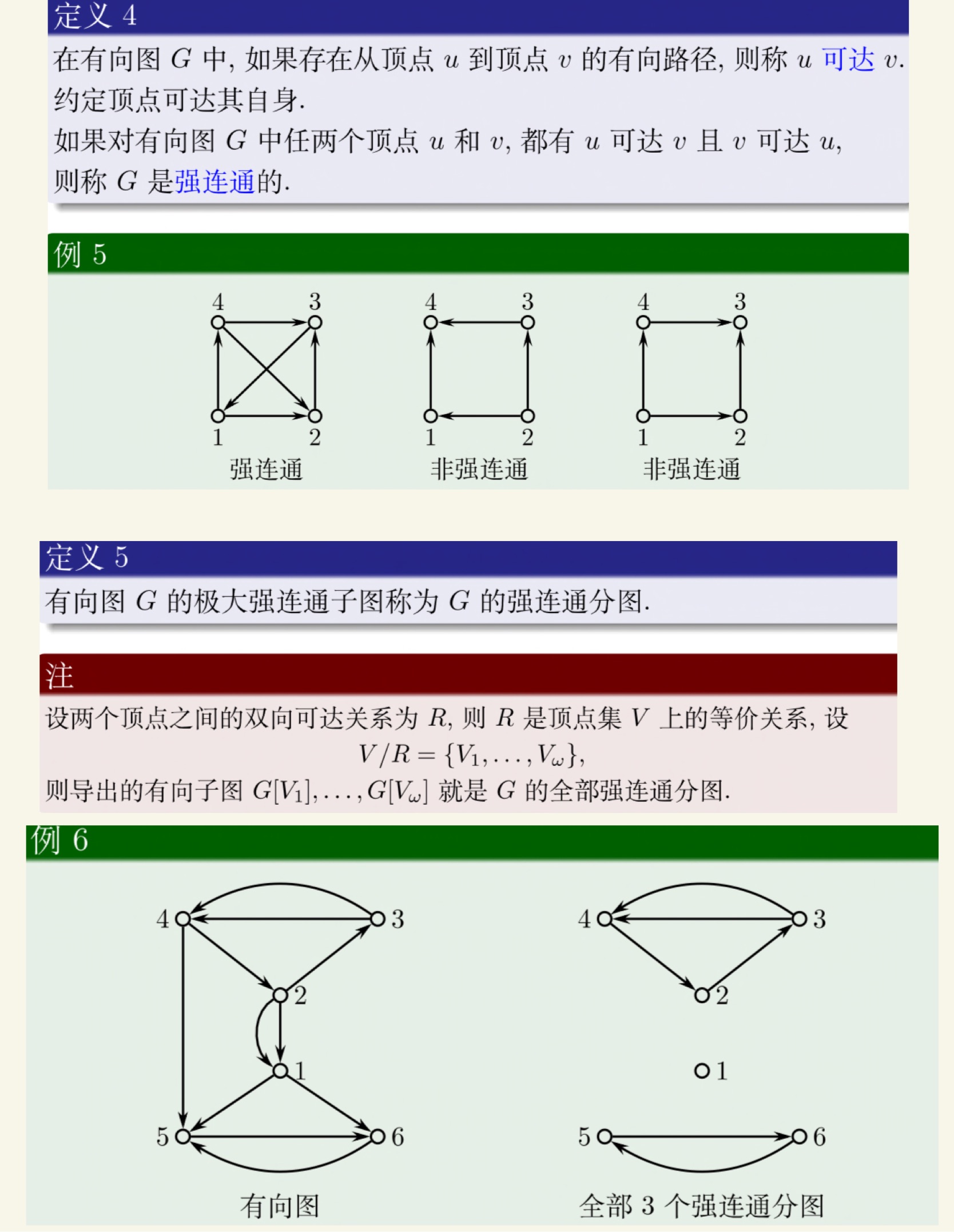
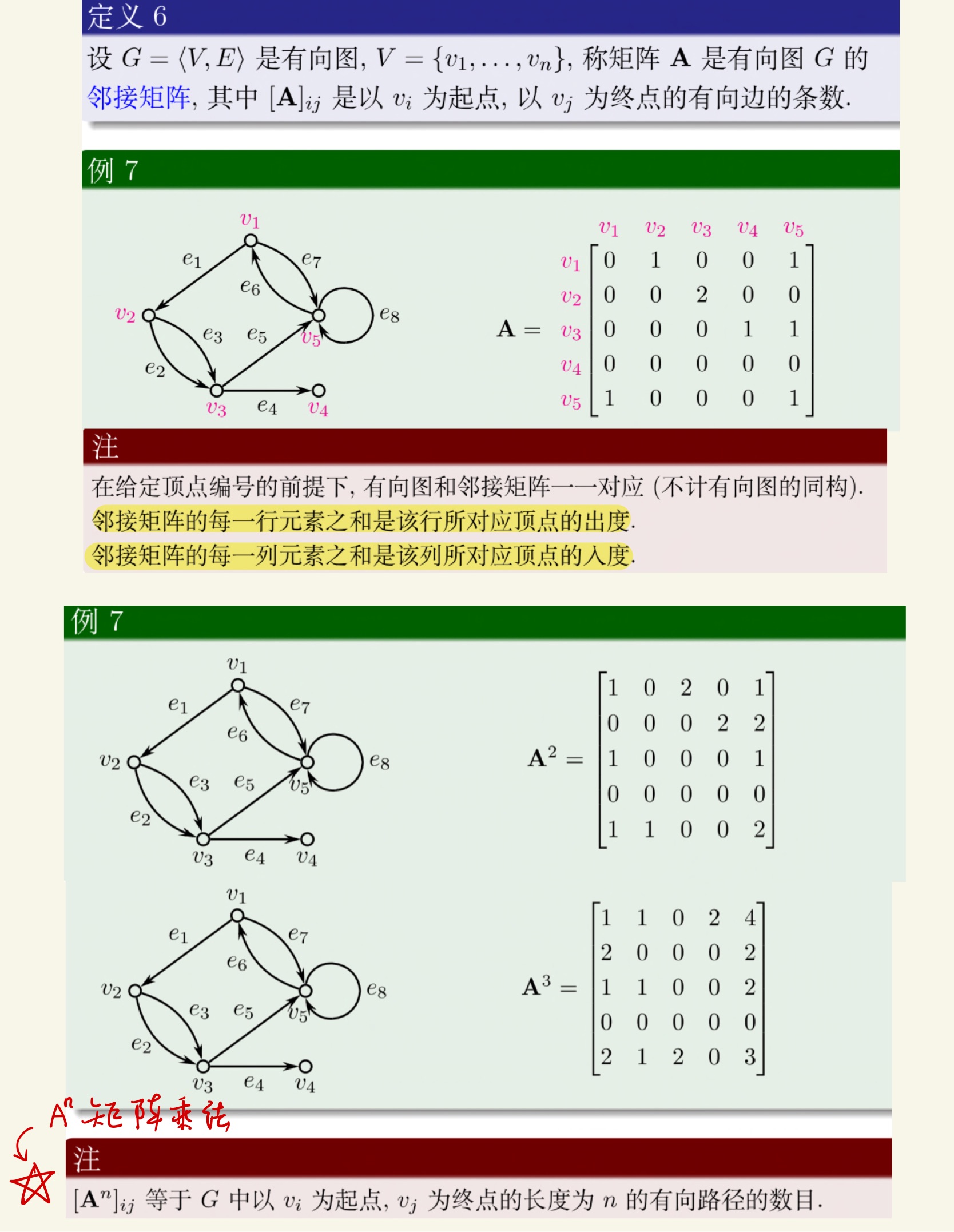
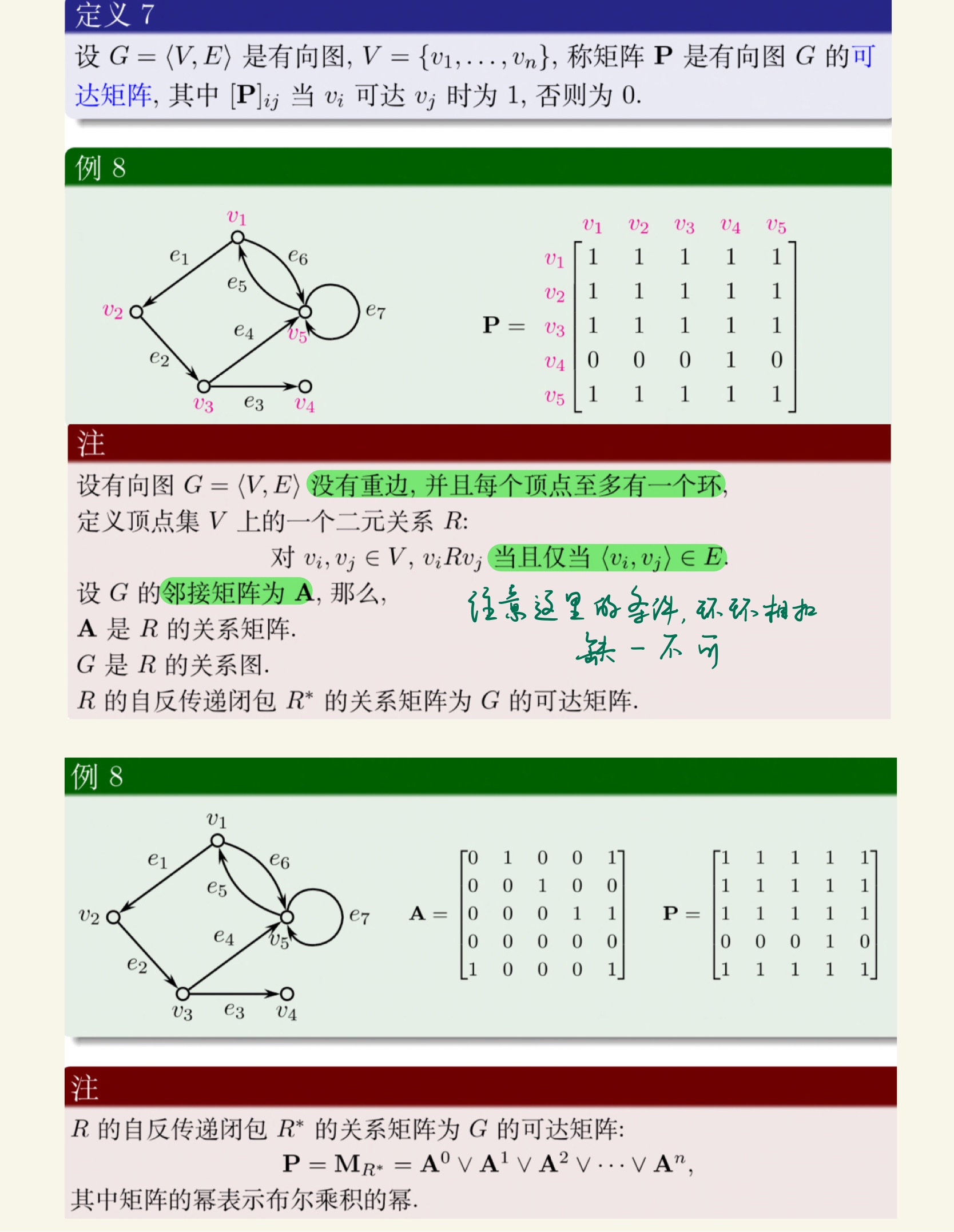
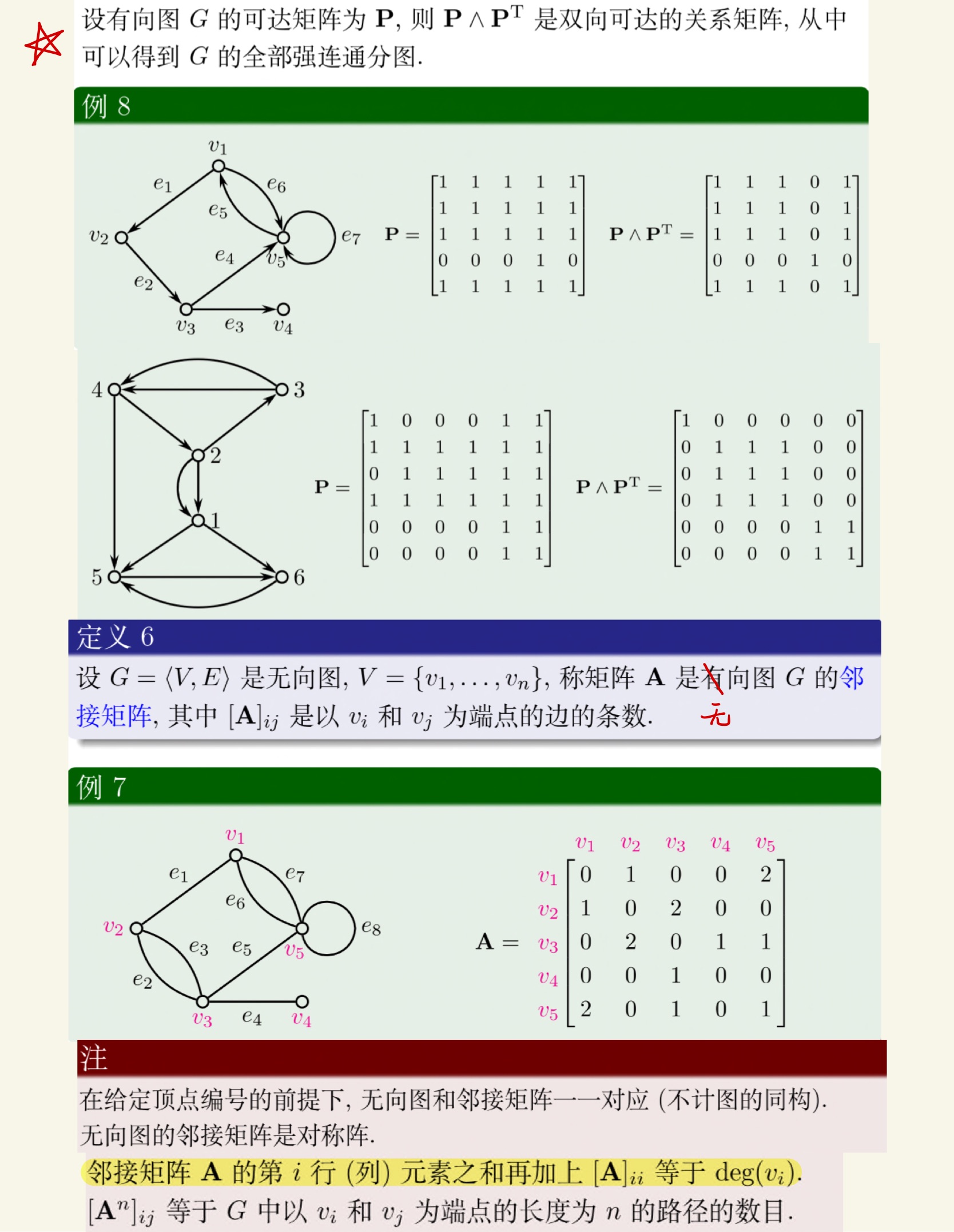
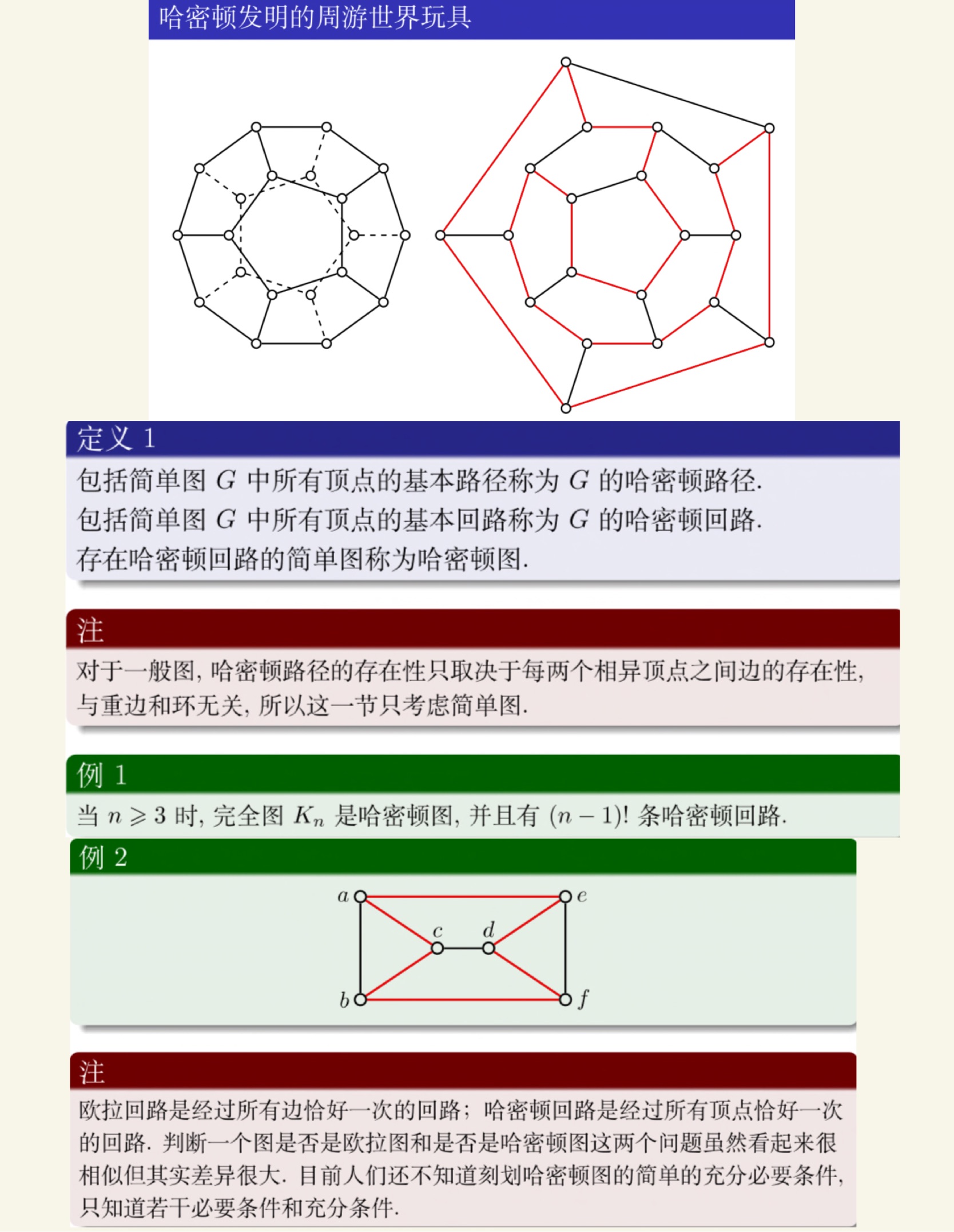
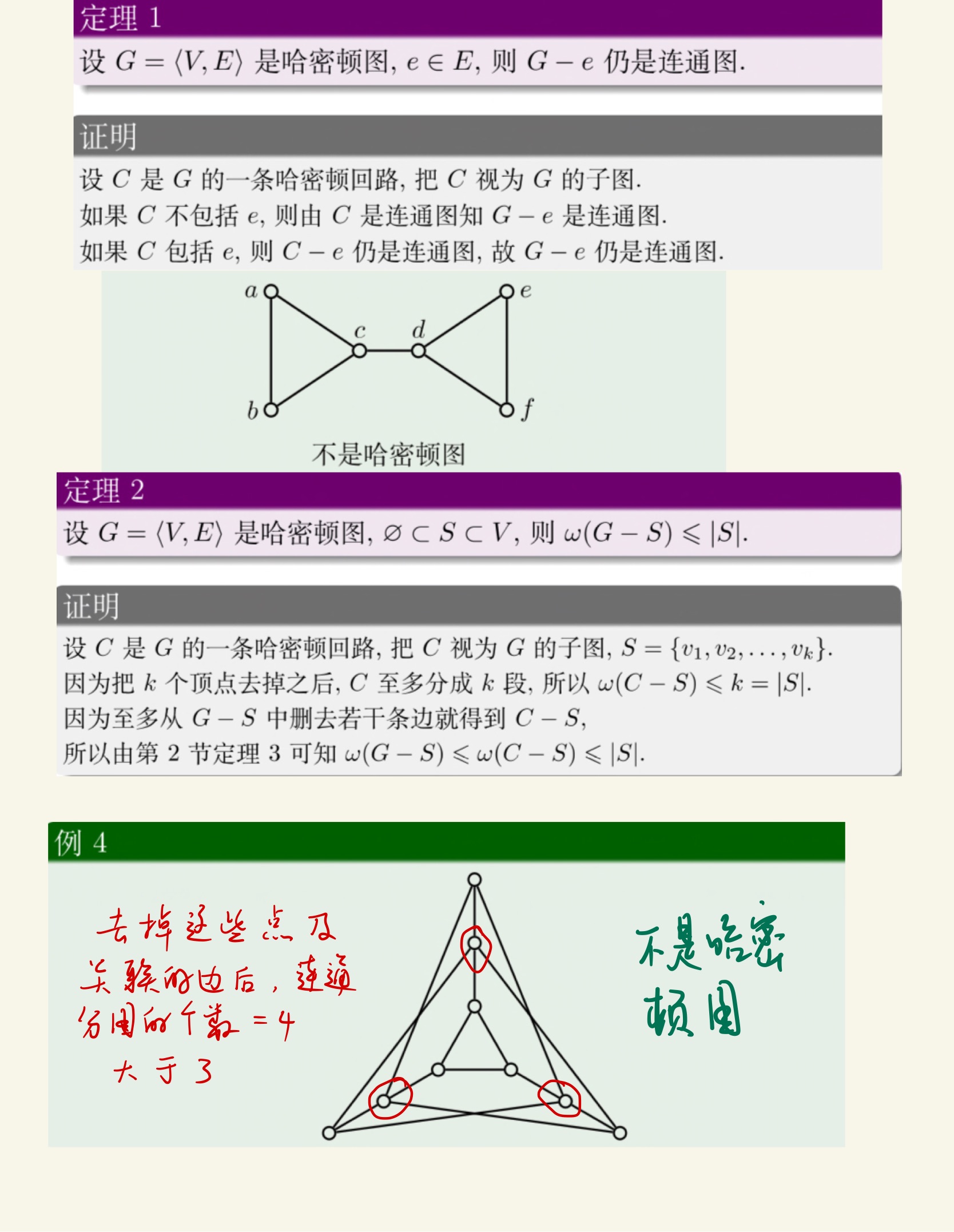
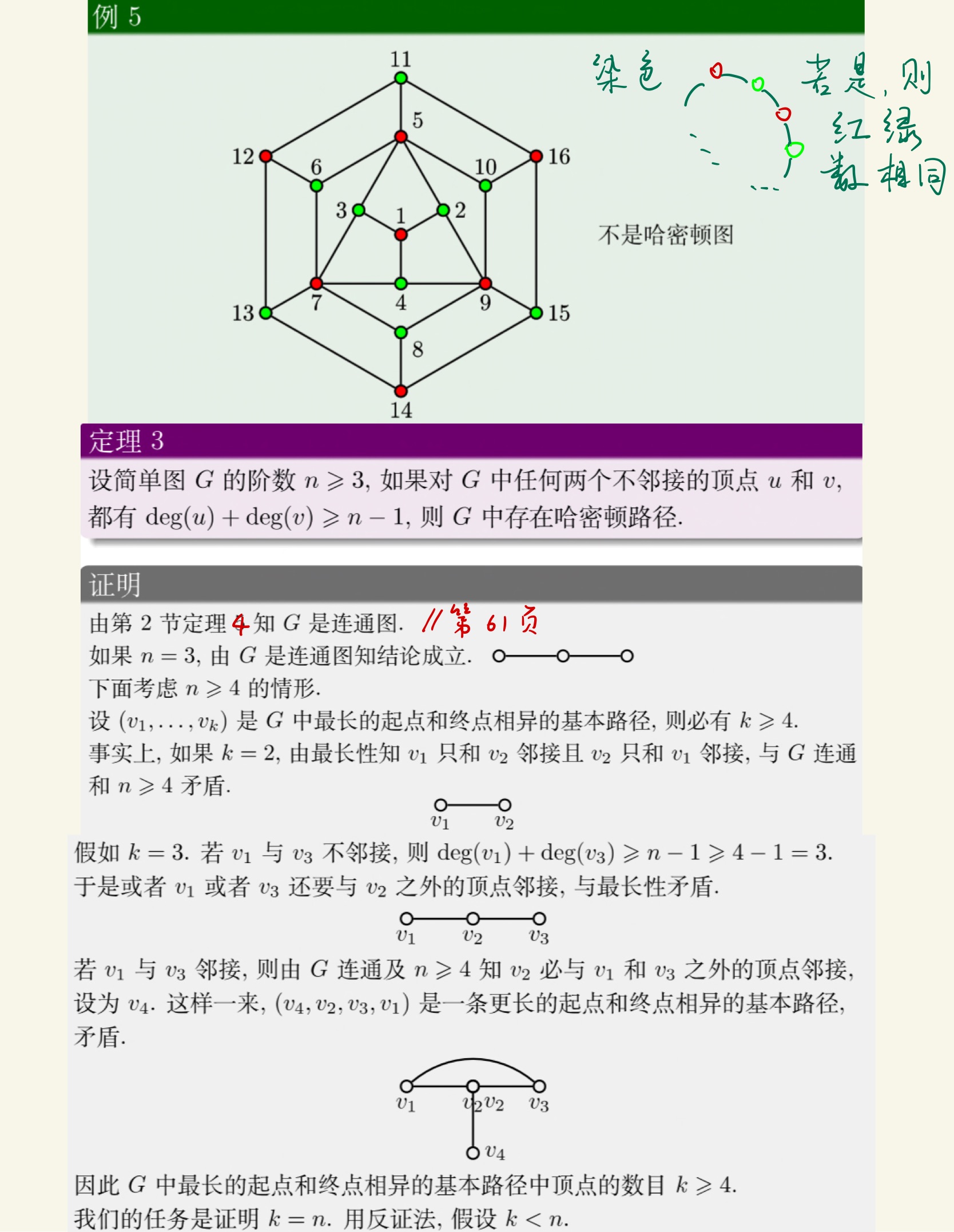
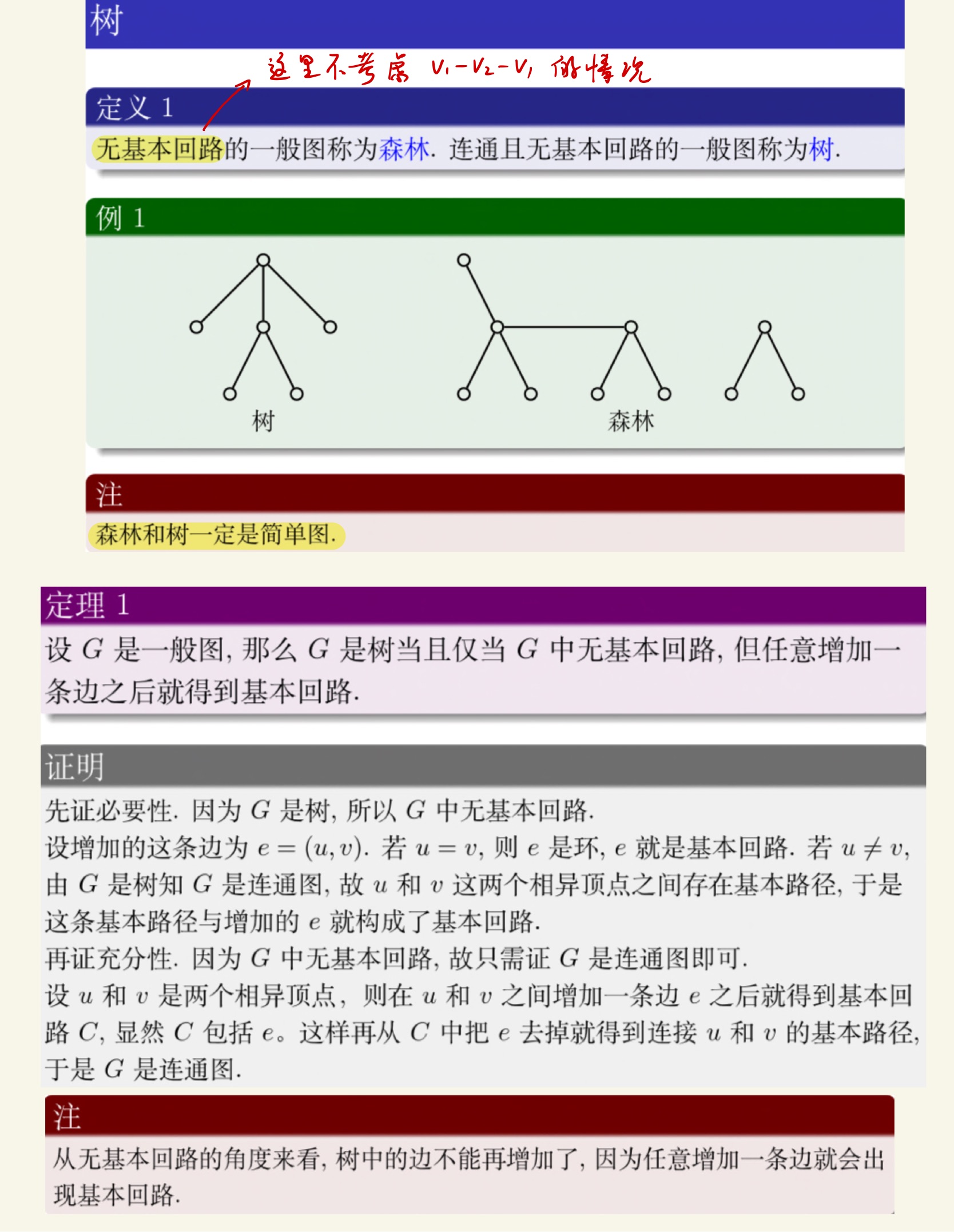
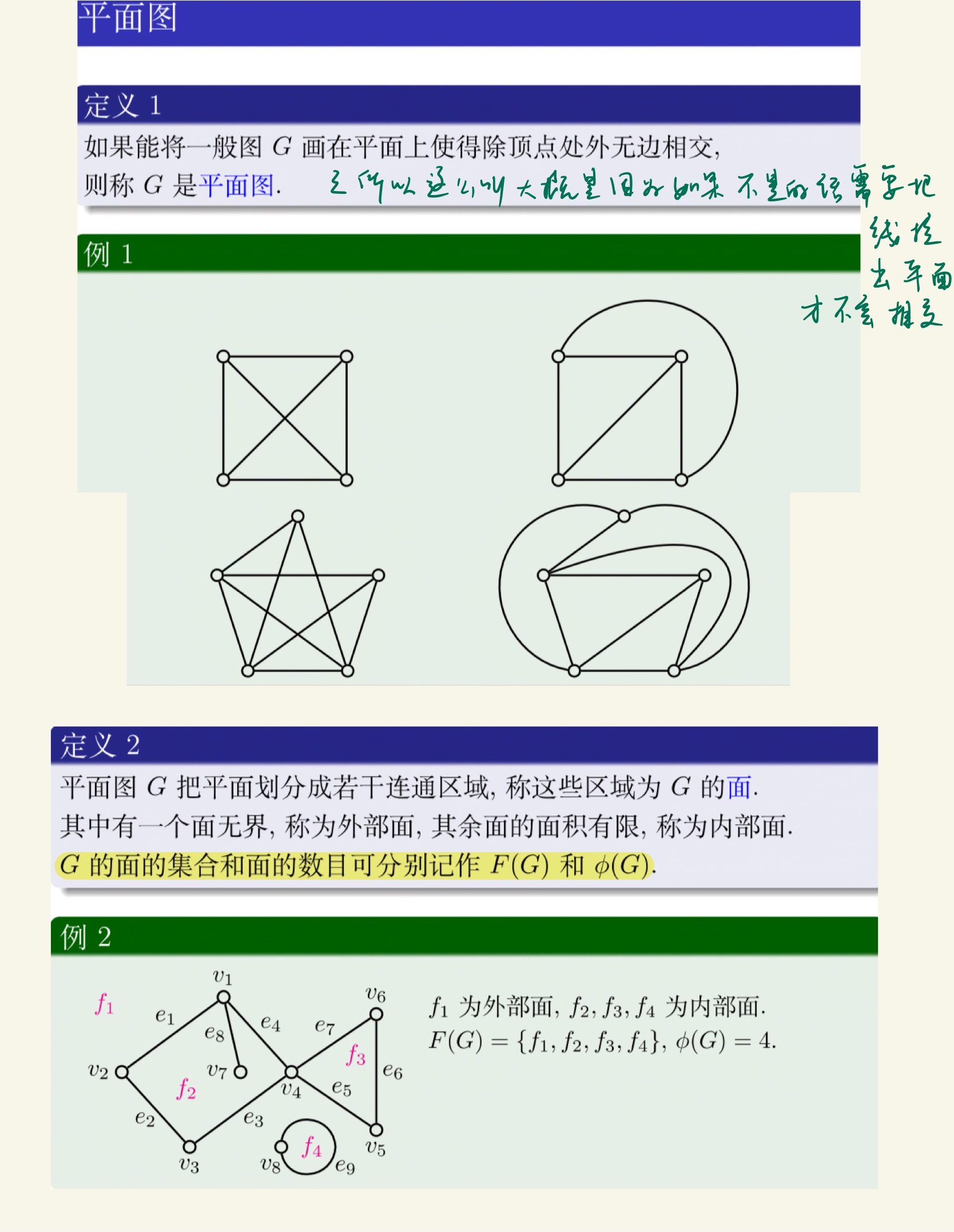
图论
老熟人了。
打问号的地方就是没看懂的地方。这一段有点奇怪,比如那一串点是拓扑排序排好的还是无所谓的呢?可能我的思路进入了莫名其妙的地方。
后日谈
前几节课都是听的线上,我根据声音脑补这是个穿着灰白上衣的瘦高老头,墙上斑驳的石灰一样。结果去了线下,才发现是个头发浓密的青年人,裹一挂蓝色的冲锋衣。有点失望。
总的来说,这老师讲的还可以。虽然可以说是念 PPT,但他 PPT 写的不错,条理清晰,比教科书好多了。草草翻了翻教科书:跟着这玩意学简直是灾难。
笔记里除了一个打红色问号的地方,其他证明都跟着推了一遍。
课程学完已是学期末尾,将要准备答辩。工作的话没有找到,毕竟这专业真的是难就业,摆烂三年多绩点难看,大环境又如此糟糕。当然,找一个达不到个税起征点的工作应该还是能行的,虽然入学的时候觉得学校不行,尤其是录到一个野鸡专业,但除开顶尖的一些人,大多数学生就业还是仰仗学校的名字的。然而,读书这么多年,出来收入和家里小学毕业的打工人差不多,多少还是有点不平衡。
天气异常炎热,草坪上的洒水管边总会聚几只乘凉的鸟雀。大学颓废的日子里想通了一些问题,但似乎也丢掉了一些对自己的勇气。
二零二三年六月九日。
极限毕业了。在教务系统的截止日期前,我催着老师批自己的卷子。这次考试似乎是整个系一张卷子,不同老师批改不同部分,虽然还有题没出分,总归是够及格分了。赶紧开了一张成绩证明,找教务处做了课程替代,把之前挂掉的某门课程改革毙掉的课程替代了。
临走时,老师朝我挥手:
“祝你顺利。”
二零二三年六月二十六日。