前置知识请见人工智能导论。

初识 TensorFlow

官网： https://www.tensorflow.org

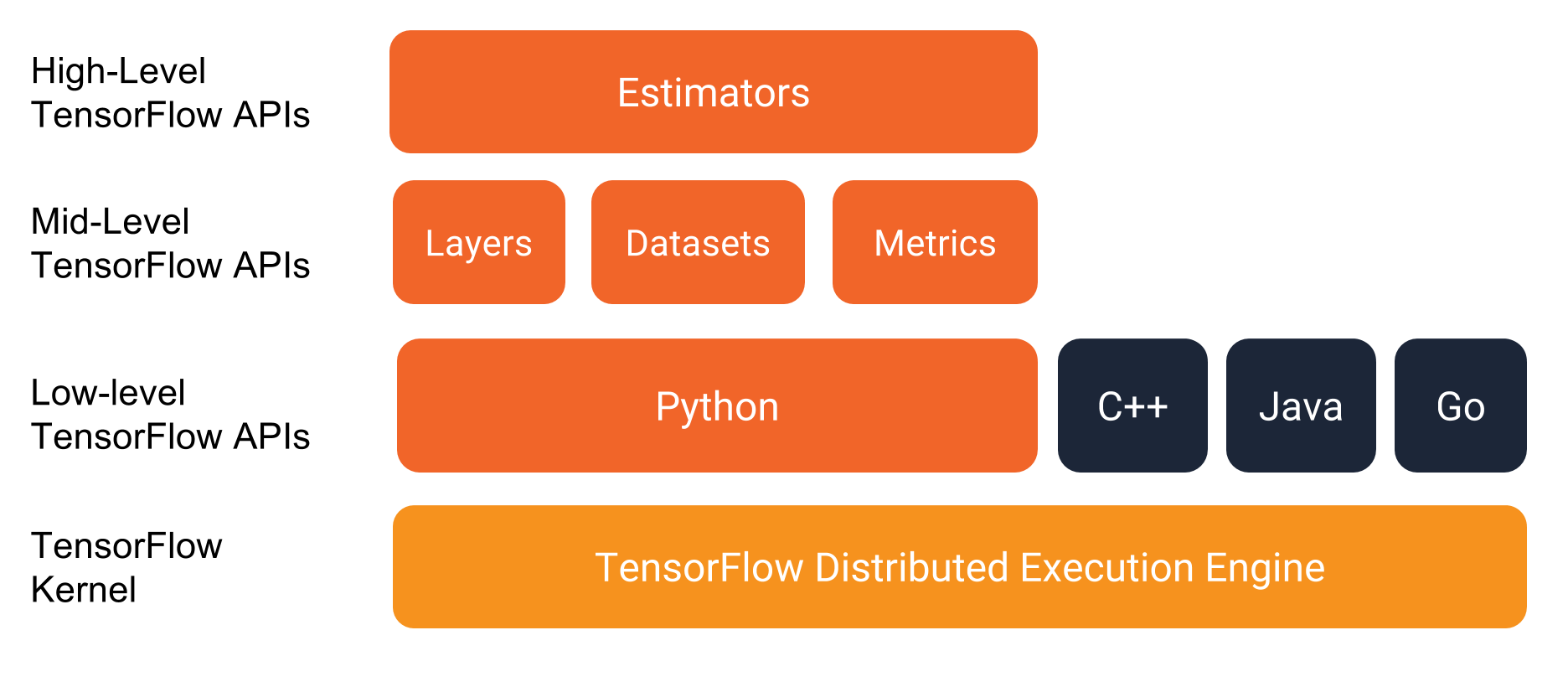
TensorFlow 大框架：

Estimator 属于 High level 的 API，而 Mid-level API 分别是：

Layers：用来构建网络结构
Datasets：用来构建数据读取 pipeline
Metrics：用来评估网络性能

Tensorflow1.0 主要特性：

XLA —— Accelerate Linear Algebra
- 提升训练速度 58 倍
- 可以在移动设备运行
引入更高级别的 API —— tf.layers / tf.metrics / tf.losses / tf.keras
Tensorflow 调试器
支持 docker 镜像，引入 tensorflow serving 服务

Tensorflow2.0 主要特性：

使用 tf.keras 和 eager mode 进行更加简单的模型构建
鲁棒的跨平台模型部署
强大的研究实验
清除不推荐使用的 API 和减少重复来简化 API

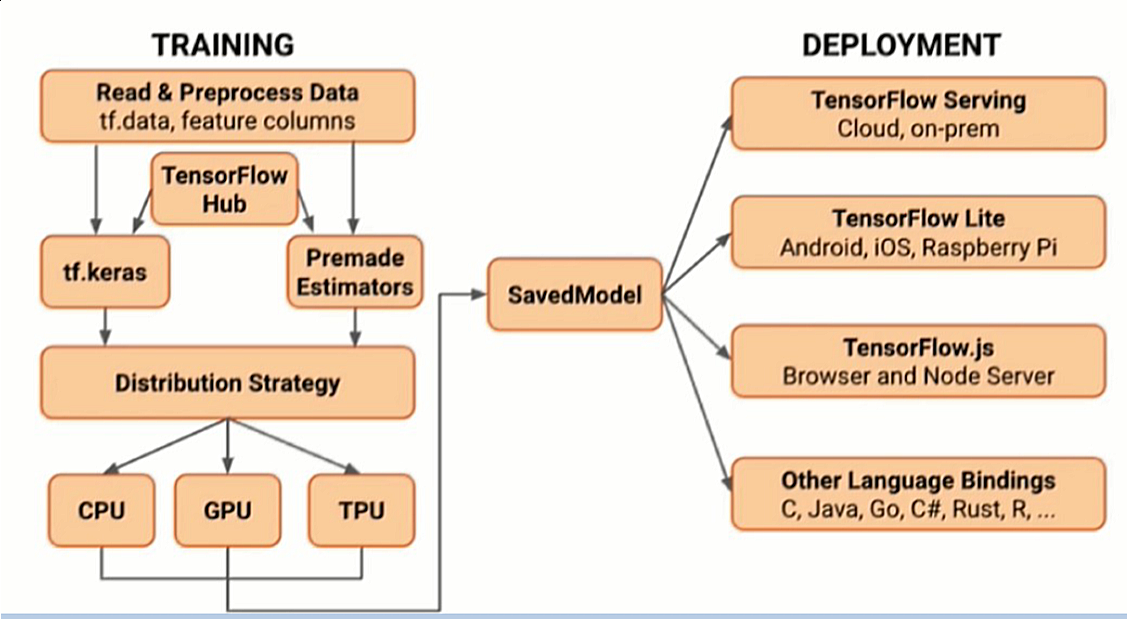
使用 Tensorflow 的大致流程：

在虚拟环境中安装 tensorflow 。

一个 helloword 程序：

import tensorflow as tf

print('*******************')
print(tf.__version__)

x = tf.constant(0.) # 常量  张量
y = tf.constant(1.)

for i in range(50):
    x = x+y
    y = y/2

print(x.numpy())  # 张量和 ndarray 之间可以互相转化
print(x)

在我本地没有 nvidia GPU 的电脑，输出类似于：

# 前面还有一大堆警告和报错...
This TensorFlow binary is optimized to use available CPU instructions in performance-critical operations.
To enable the following instructions: AVX2 AVX_VNNI FMA, in other operations, rebuild TensorFlow with the appropriate compiler flags.
*******************
2.19.0
[时间]E external/local_xla/xla/stream_executor/cuda/cuda_platform.cc:51] failed call to cuInit: INTERNAL: CUDA error: Failed call to cuInit: UNKNOWN ERROR (303)
2.0
tf.Tensor(2.0, shape=(), dtype=float32)

在 Colab 中运行该代码，得到输出：

*******************
2.18.0
2.0
tf.Tensor(2.0, shape=(), dtype=float32)

另一个例子：

import tensorflow as tf

print('*******************')
print(tf.__version__)

x = tf.Variable(0.) # 变量  张量
y = tf.Variable(1.)

print(x)
print(y)

x.assign(x+y)

print(x)
print(y)

'''
前略
*******************
2.19.0
[时间]: E external/local_xla/xla/stream_executor/cuda/cuda_platform.cc:51] failed call to cuInit: INTERNAL: CUDA error: Failed call to cuInit: UNKNOWN ERROR (303)
<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=0.0>
<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=1.0>
<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=1.0>
<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=1.0>
'''

图结构：静态图，效率高；动态图，调试容易。

图（graph） 是 tensorflow 用于表达计算任务的一个核心概念。从前端（Python）描述神经网络的结构，到后端在多机和分布式系统上部署，到底层 Device（CPU、GPU、TPU）上运行，都是基于图来完成。

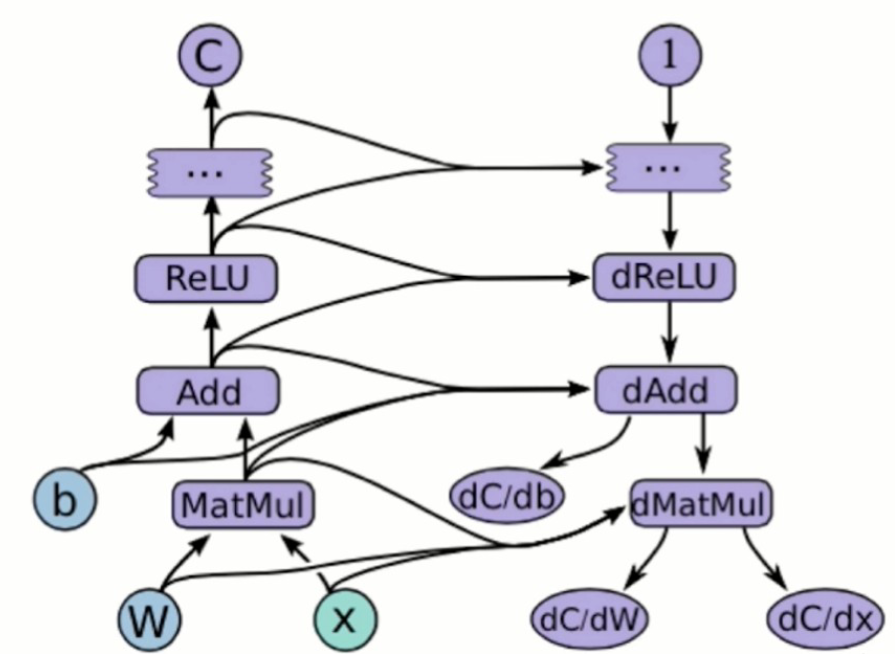
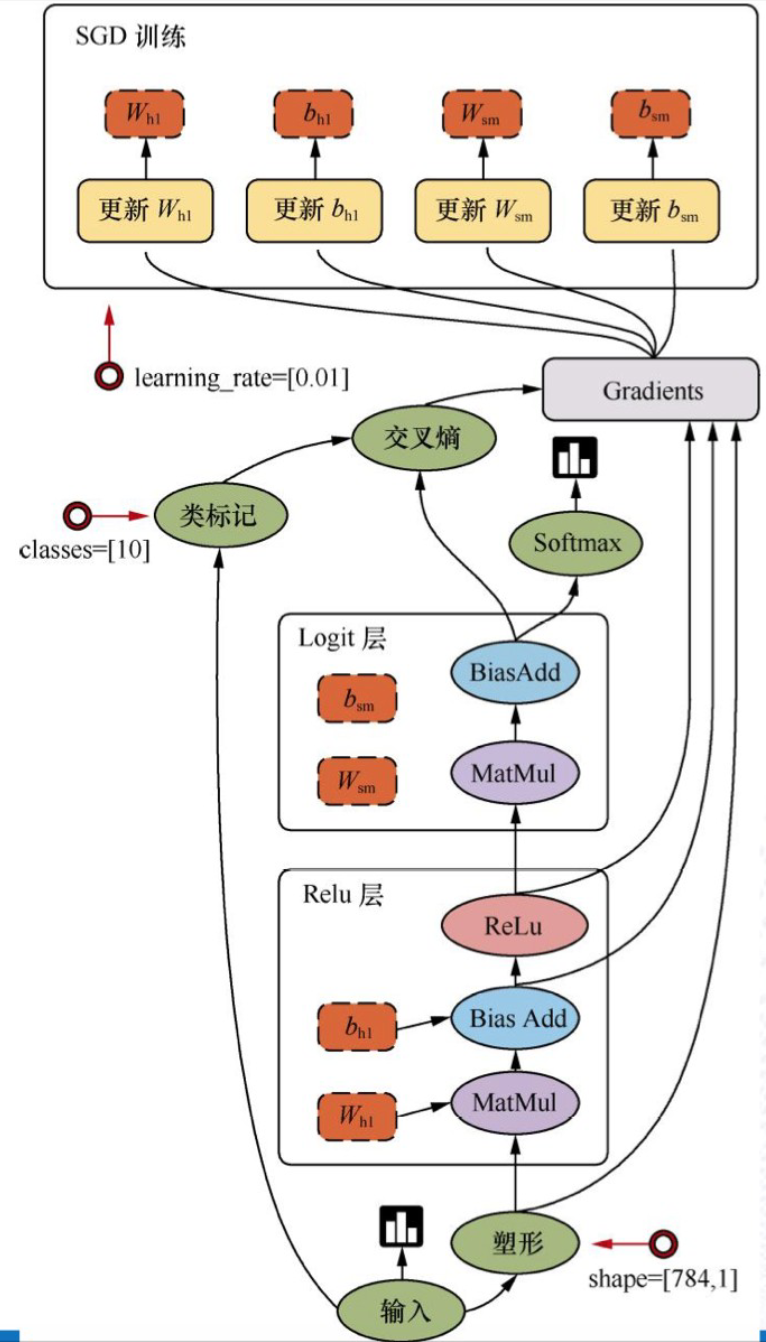
数据流图：

张量为什么那么多阶？
可以考虑一些典型场景。例如，灰度图、png、视频等。

深度学习中的“张量” 是工程实践中使用的多维数组结构，而 数学中的张量 是抽象代数与几何的核心概念，两者在形式上相似，但本质和用途大不相同。

张量属性：

graph 张量所属的默认图
op 张量的操作名
name 张量的字符串描述
shape 张量形状

Tensorflow-keras

简介

keras 是基于 python 的高级神经网络 API，以 Tensorflow、CNTK 或 Theano 为后端运行，keras 必须有后端才可以运行。后端可以切换，现在多用 tensorflow. 方便快速实验，帮助用户以最少的时间验证自己的想法。

Tensorflow-keras 是什么？

Tensorflow 对 keras API 规范的实现
相对于以 tensorflow 为后端的 keras, Tensorflow-keras 与 Tensorflow 结合更加紧密
实现在 tf.keras 空间下

Tf-keras 和 keras 联系：

基于同一套 API
keras 程序可以通过修改导入方式轻松转为 tf.keras 程序
反之可能不成立，因为 tf.keras 有其他特性
相同的 JSON 和 HDF5 模型序列化格式和语义

tf_keras做分类

下面的 ipynb 文件包含以下内容：

一个衣服分类的实验
为什么要分为训练集，验证集，测试集
tensorflow 的基本使用
均方误差
Cross Entropy Loss Function（交叉熵损失函数）
w 的初始分布

下面的 ipynb 文件包含以下内容：

对之前相同的流程，做归一化，看看有无改进

下面的 ipynb 文件包含以下内容：

TensorBoard
ModelCheckpoint
EarlyStopping

tf_keras做回归

下面的 ipynb 文件包含以下内容：

使用 California Housing dataset 做回归

梯度消失、梯度爆炸

问题描述

关于梯度消失，从一个例子入手：

上面文件演示的问题即是梯度消失。

梯度消失：
梯度消失问题发生时，接近于输出层的 hidden layer 3 等的权值更新相对正常，但前面的 hidden layer 1 的权值更新会变得很慢，导致前面的层权值几乎不变，仍接近于初始化的权值，这就导致 hidden layer 1 相当于只是一个映射层，这是此深层网络的学习就等价于只有后几层的浅层网络的学习了。

梯度爆炸：
在反向传播过程中使用的是链式求导法则，如果每一层偏导数都大于 1，那么连乘起来将以指数形式增加，误差梯度不断累积，就会造成梯度爆炸。梯度爆炸会导致模型权重更新幅度过大，会造成模型不稳定，无法有效学习，还会出现无法再更新的 NaN 权重值。

梯度消失和梯度爆炸其实都是因为反向传播中的连乘效应。除此之外，也和激活函数的选取有关。

$\text{selu}(x) = \lambda \begin{cases} x & \text{if } x > 0 \\ \alpha e^x - \alpha & \text{if } x \leq 0 \end{cases}$

对于梯度消失：

Sigmoid 函数的导数最大值是 0.25（当 $ z = 0 $ 时）。当 $ z $ 的绝对值较大时（即神经元饱和时），$ \sigma’(z) $ 接近于 0 .
Tanh 函数，当 $ z $ 的绝对值较大时，导数也接近于 0 .
在反向传播过程中，如果许多层的激活函数导数值都小于1（特别是当它们远小于1时，比如 Sigmoid 导数的最大值0.25），这些导数值连乘起来会使梯度呈指数级衰减。
如果权重被初始化为较小的值（例如，绝对值小于 1），多个较小的权重矩阵与较小的激活函数导数连乘，会进一步加速梯度的消失。

对于梯度爆炸，可以作类似的解释，不再赘述。

批归一化

接下来的行文逻辑：什么是批归一化，批归一化的动机，减均值除以标准差为什么失败，正确的批归一化算法。

批归一化可以缓解梯度消失和梯度爆炸的问题，简单来说即是，每层的激活值都做归一化。

在深度神经网络的训练过程中，每一层的参数都会在反向传播后进行更新。这意味着，对于网络中的某一层，其输入数据的分布（来自前一层的输出）会随着训练的进行而不断发生变化。这种现象被称为内部协变量偏移 (Internal Covariate Shift, ICS)。

ICS 会导致以下问题：

训练速度减慢：后续层需要不断适应这种变化的输入分布。
对初始化敏感：网络对参数的初始值更加敏感。
激活函数饱和：输入数据分布的变化可能导致激活函数的输入落入饱和区（例如Sigmoid的两端），从而导致梯度消失。

批归一化的提出就是为了缓解 ICS 问题。

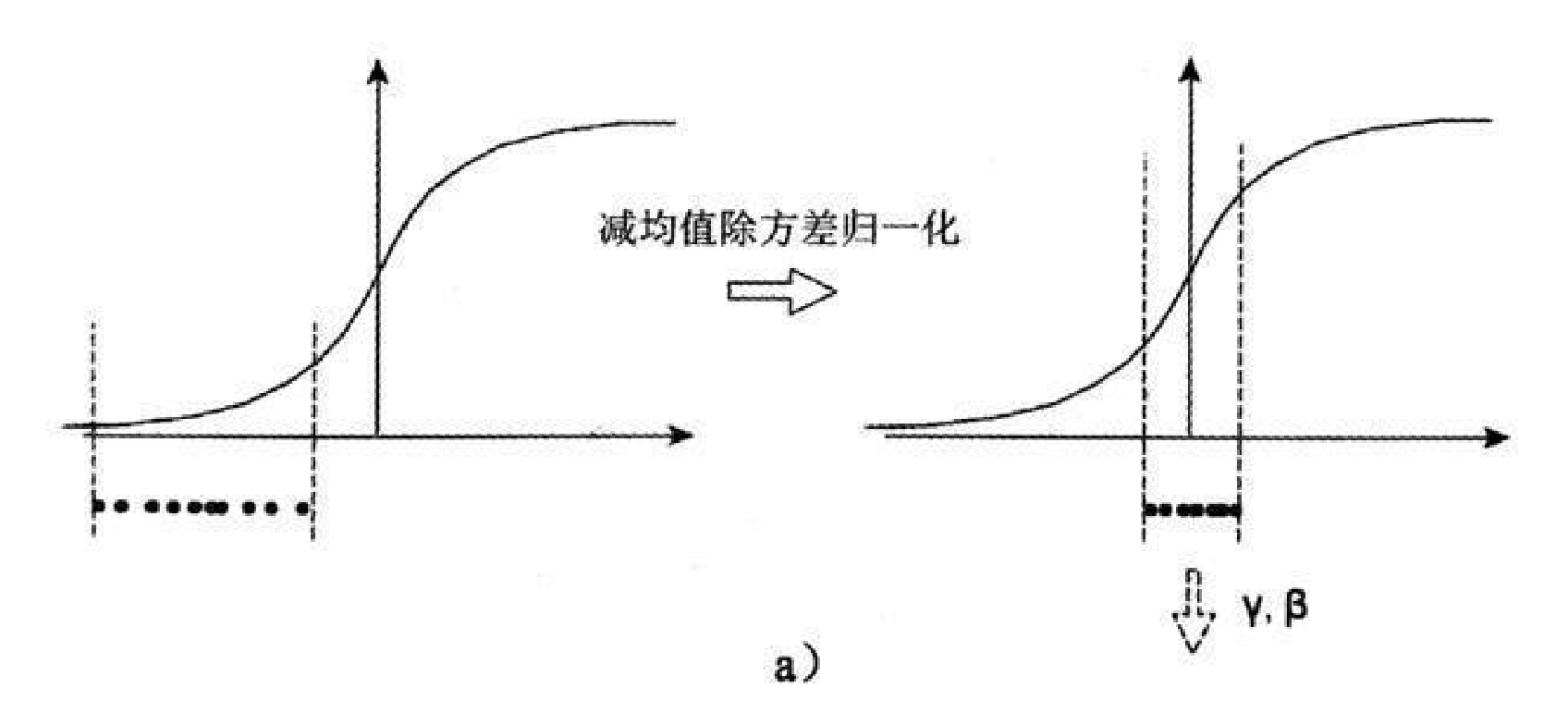
如何实现批归一化呢？我们自然想到经典的“减均值除以标准差”方法：

这有两个好处：

避免分布数据偏移
远离导数饱和区

但这个处理对于在 -1~1 之间的梯度变化不大的激活函数，效果不仅不好，反而更差。比如 sigmoid 函数，在 -1~1 之间几乎是线性，BN 变换后就没有达到非线性变换的目的；而对于 relu，效果会更差，因为会有一半的置零。总之，减均值除以标准差后可能削弱网络的性能。

改进的思路是：缩放加移位。

这里的 $ y_i $ 就是批归一化层的输出，它将作为下一层或激活函数的输入。$\gamma$ 和 $\beta$ 是与网络的其他参数（如权重 $ W $ 和偏置 $ b $）一样通过梯度下降学习得到的。如果网络发现原始的表示更好，它可以学习到 $\gamma = \sqrt{\sigma_B^2 + \epsilon}$ 和 $\beta = \mu_B$，从而在一定程度上抵消归一化的影响。

tensorflow 中的接口：
https://www.tensorflow.org/api_docs/python/tf/keras/layers/BatchNormalization

下面是使用批归一化的例子：

更改激活函数

relu -> selu, 缓解梯度消失。

实例：

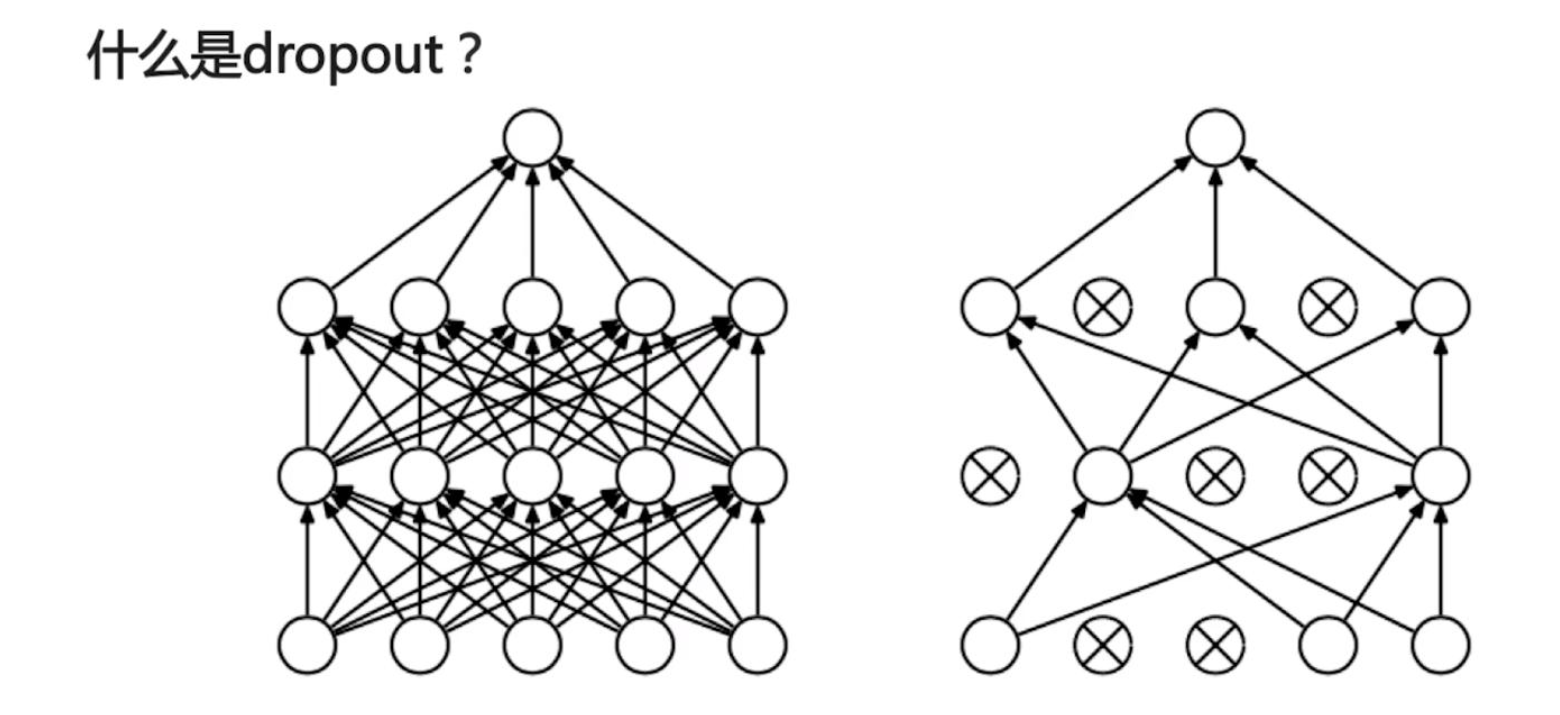
Dropout

Dropout 可以防止过拟合，实现也非常简单：对想要 dropout 的点输出乘 0 .

在 tensorflow keras 中的实现：

The Dropout layer randomly sets input units to 0 with a frequency of rate at each step during training time, which helps prevent overfitting. Inputs not set to 0 are scaled up by 1 / (1 - rate) such that the sum over all inputs is unchanged.

实例：

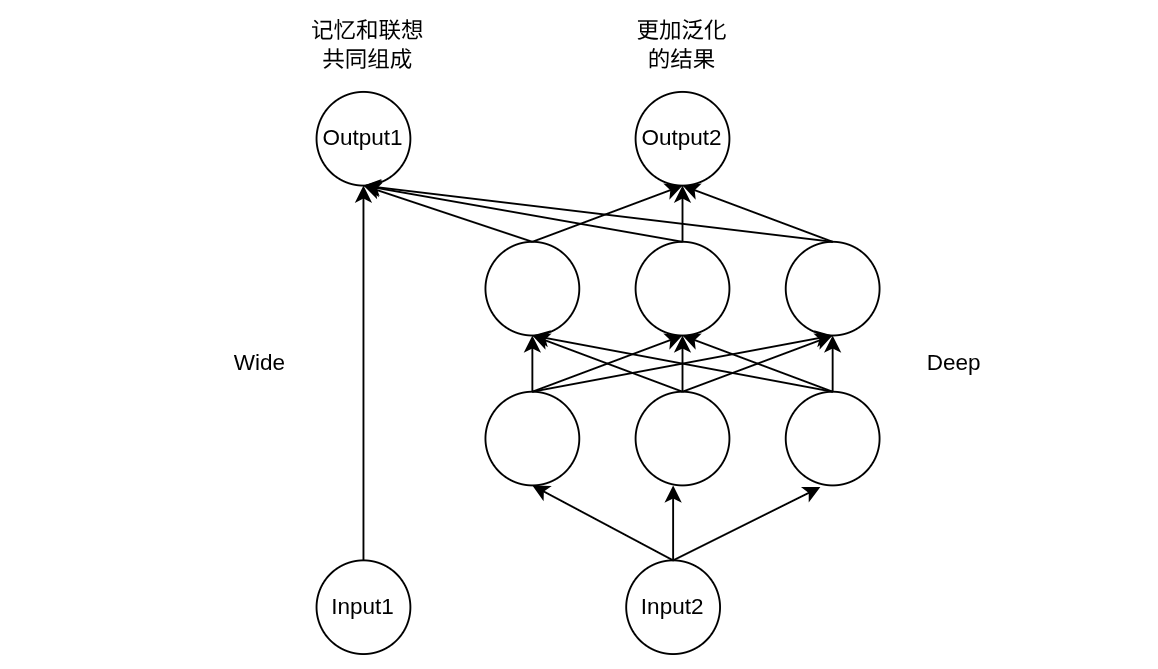
Wide & Deep 模型（推荐场景）

原始论文: https://arxiv.org/pdf/1606.07792v1

Google 于 16 年发布，用于分类和回归。曾应用在 Google Play 中的应用推荐。

Wide 用于记忆，Deep 用于联想。一个推荐系统的经典矛盾：应该给用户推荐经常买的，还是探索一些用户可能会买的？

https://blog.csdn.net/Yasin0/article/details/100736420 （已备份）
https://zhuanlan.zhihu.com/p/57247478
https://zhuanlan.zhihu.com/p/139358172 （已备份）

尝试搭建简单的 wide and deep 模型（github 链接）：

在 Deep 部分，会用到 Word2Vec 技术。简要介绍：

Word2Vec is a technique in natural language processing that represents words as vectors in a high-dimensional space, capturing semantic relationships between them. It essentially translates words into numerical representations, where words with similar meanings are located closer together in the vector space.

可供参考的资料：
https://medium.com/@manansuri/a-dummys-guide-to-word2vec-456444f3c673

Word2Vec utilizes two main architectures:

CBOW (Continuous Bag of Words): Predicts a target word based on its surrounding context words.
Skip-gram: Predicts surrounding words based on a given input word.

简要的原理介绍：
如何衡量两个词在语义上是否相近？如果两个词的上下文相同（相近），我们可以有较大的把握认为，这两个词的语义也相近。我们构造一个神经网络，输入为上下文，输出为该词，训练之，将隐藏层的数值作为这个词的 vector 元素。在实践中，我们发现语义相近的词，由这种机制产生的 vector 表示也相近。

有了 Word2Vec，我们就可以用向量之间的差距来衡量信息之间的差距。

用面向对象的方法重写之前的代码：github链接。

在之前的模型中，我们只有一个输入，现在尝试多输入（github链接）：

iframe 嵌多了可能有点卡，之后只放 github 链接了。

尝试搭建更加复杂的模型（github链接）：

一个关于 Wide and Deep 的推荐实验：
https://blog.csdn.net/weixin_34268753/article/details/92123569

超参数搜索

为什么要超参数搜索？手工去试耗费人力。

有哪些超参数？

网络结构参数：几层，每层神经元个数，每层激活函数
训练参数: batch_size，学习率，学习率衰减算法

Batch Size

下面链接详细讲解了 Batch Size：
https://blog.csdn.net/qq_34886403/article/details/82558399

注意：Batch Size 增大了，要到达相同的准确度，必须要增大 epoch。

学习率衰减

固定学习率时，当到达收敛状态时，会在最优值附近一个较大的区域内摆动；而当随着迭代轮次的增加而减小学习率，会使得在收敛时，在最优值附近一个更小的区域内摆动（之所以曲线震荡朝向最优值收敛，是因为在每一个 mini-batch 中都存在噪音）。

学习率衰减算法有很多，这里仅举最简单的两例。

离散下降（discrete staircase）

对于深度学习来说，每 t 轮学习，学习率减半。对于监督学习来说，初始设置一个较大的学习率，然后随着迭代次数的增加，减小学习率。

指数减缓（exponential decay）

对于深度学习来说，学习率按训练轮数增长指数差值递减。例如：

$\alpha = 0.95^{\text{epochnum}} \cdot \alpha_0$

又或者公式为：

$\alpha = \frac{k}{\sqrt{\text{epochnum}}}$

其中 epochnum 为当前 epoch 的迭代轮数。不过第二种方法会引入另一个超参 k。

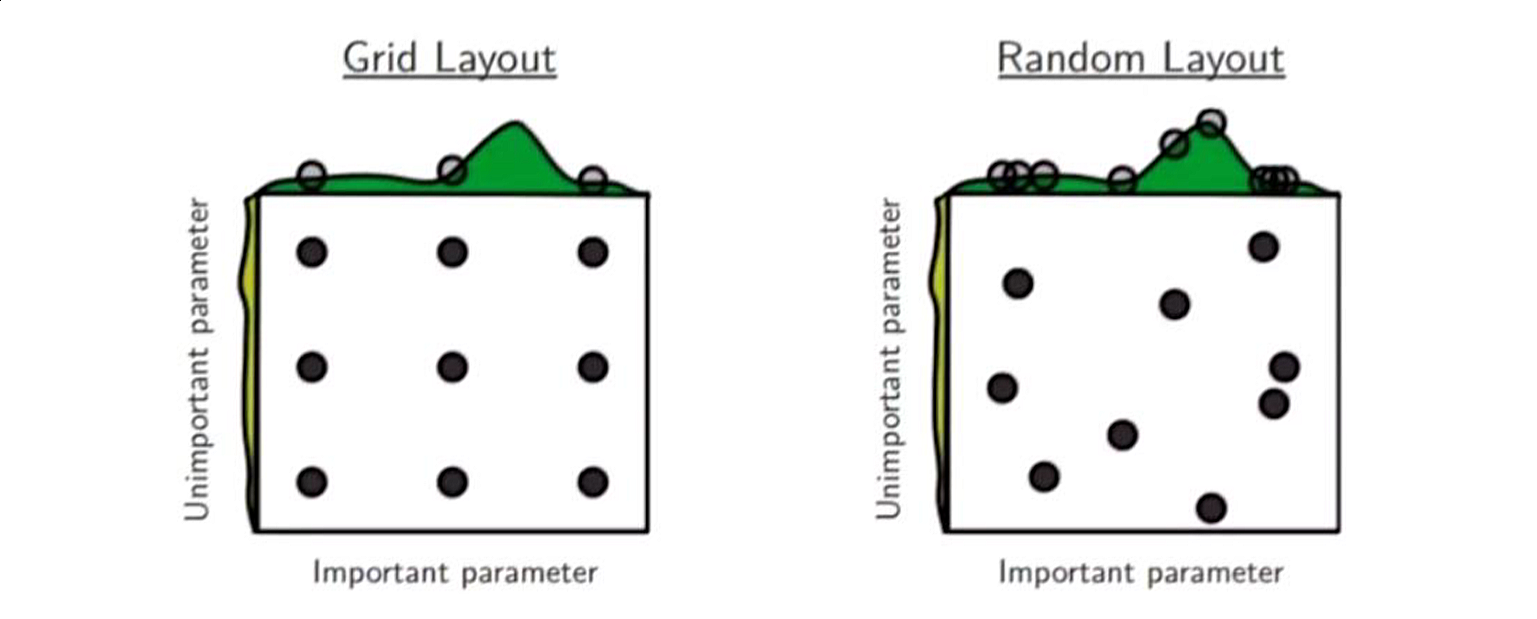
网格搜索、随机搜索

在机器学习笔记中已经提过，我们直接实战。

先看一个朴素的例子：github链接。

能否配合 sklearn 进行参数搜索？

注意： scikit-learn 在 1.6 版本中对其内部处理 estimator tags (估计器标签) 的 API 进行了现代化更改。这导致一些第三方库（包括早期版本的 XGBoost 和 CausalML）在与 scikit-learn 1.6.x 交互时出现了 AttributeError: 'super' object has no attribute '__sklearn_tags__' 类似的问题。

一种不够优雅的解决方案是降级 scikit-learn, ~~我就不尝试了。~~ github链接 .

另外一些可能的方案有：KerasTuner 等。

关于网格搜索、随机搜索：

随机搜索：参数的生成方式为随机，可探索的空间更大。

tensorflow 基础 API

本 notebook 包含以下内容：

常量张量及其操作
矩阵乘法
RaggedTensor
SparseTensor
变量张量
reduce_mean

本 notebook 包含以下内容：

自定义损失函数

本 notebook 包含以下内容：

自定义全连接层
- 重写 __init__
- 重写 build，compile 的时候就会调用 build
- 重写 call

本 notebook 包含以下内容：

@tf.function
@tf.py_function
把 py 实现的函数变为图实现的函数
找回原来的 py 函数
查看 tf 的图的代码

本 notebook 包含以下内容：

导数、偏导数的近似计算
with tf.GradientTape() as tape
二阶导数
模拟梯度下降算法

本 notebook 包含以下内容：

手动模拟 fit 操作
tf.squeeze()

dataset

本 notebook 包含以下内容：

dataset 的基本常识

本 notebook 包含以下内容：

在 kaggle 平台上操作数据
数据存为csv文件
tf.data.Dataset.list_files
tf.io.decode_csv
.shuffle()

本 notebook 包含以下内容：

为什么使用 TFRecord
tf.train.BytesList, tf.train.FloatList, tf.train.Int64List
tf.train.Features, tf.train.Example
读取 record 并打印
把 tfrecord 存为压缩文件

数据保存为 tfrecord, 然后再读出来训练： notebook

estimator

Estimator API 是 TensorFlow 1.x 时代的主要训练方式，现在为了简化和统一，官方推荐直接使用 Keras 的 model.fit(), model.evaluate(), model.predict() .

即便如此，我保留了一些有价值的代码片段。

本 notebook 包含以下内容：

使用 titanic 数据集
将特征预处理作为模型的一部分，使得模型部署和迁移都更加方便
- StringLookup, CategoryEncoding

本 notebook 包含以下内容：

旧范式，仅参考

卷积神经网络

什么是卷积神经网络？

(卷积层+(可选)池化层)×N+全连接层×M ,N>=1, M>=0
卷积层的输入和输出都是矩阵，全连接层的输入和输出都是向量

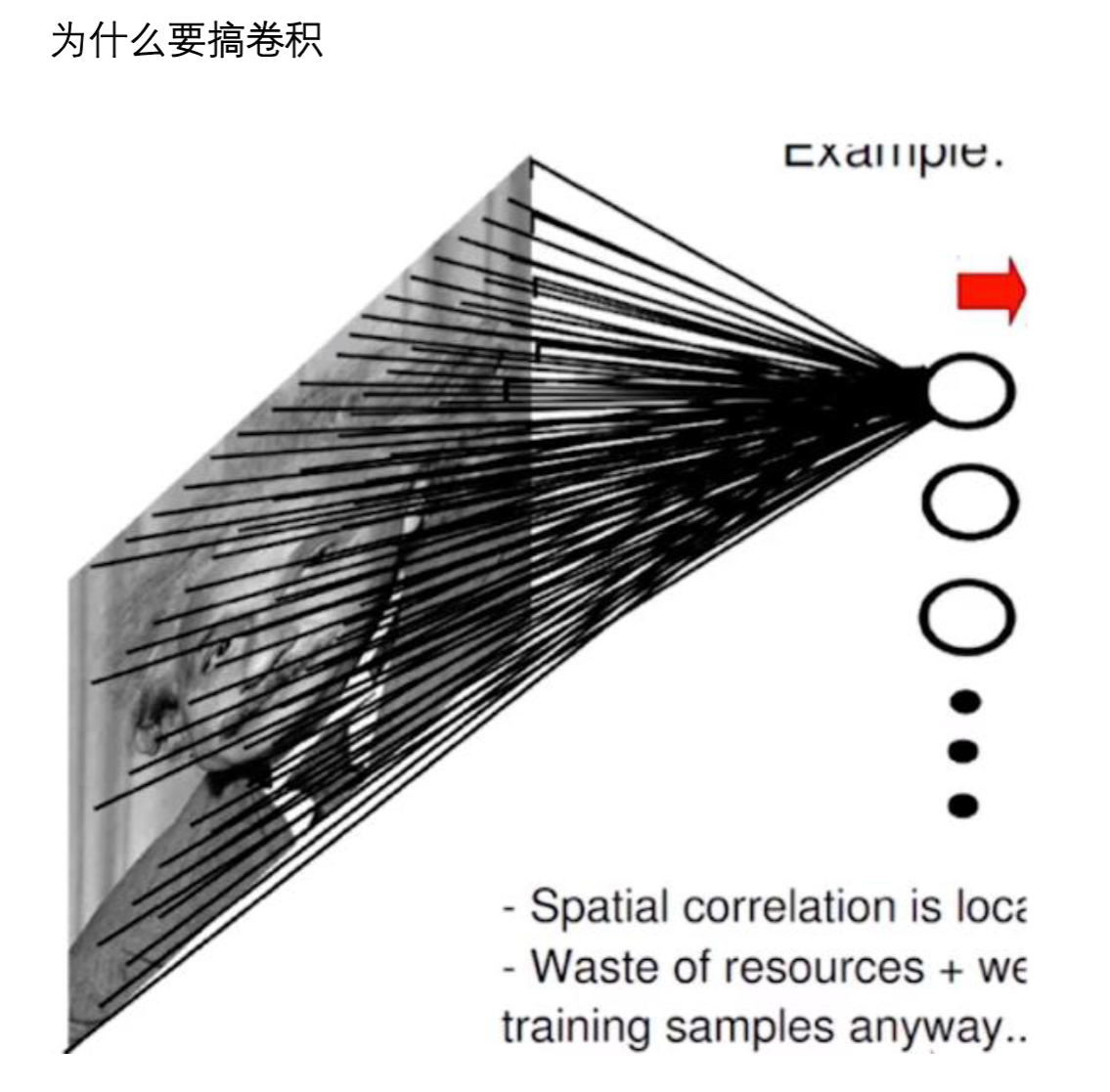
全连接层的困境

上图中，图像大小 1000×1000，一层神经元数目为 10^6（经验：神经元数目应与特征数的数量差不多，这样效果好），这样全连接参数为 1000*1000*10^6 = 10^12，一层就是 1 万亿个参数，内存装不下。

除此之外，全连接层还有参数过多容易过拟合的问题：

计算资源不足
容易过拟合，发生过拟合，我们就需要更多训练数据，但是很多时候我们没有更多的数据，因为获取数据需要成本

卷积的思路

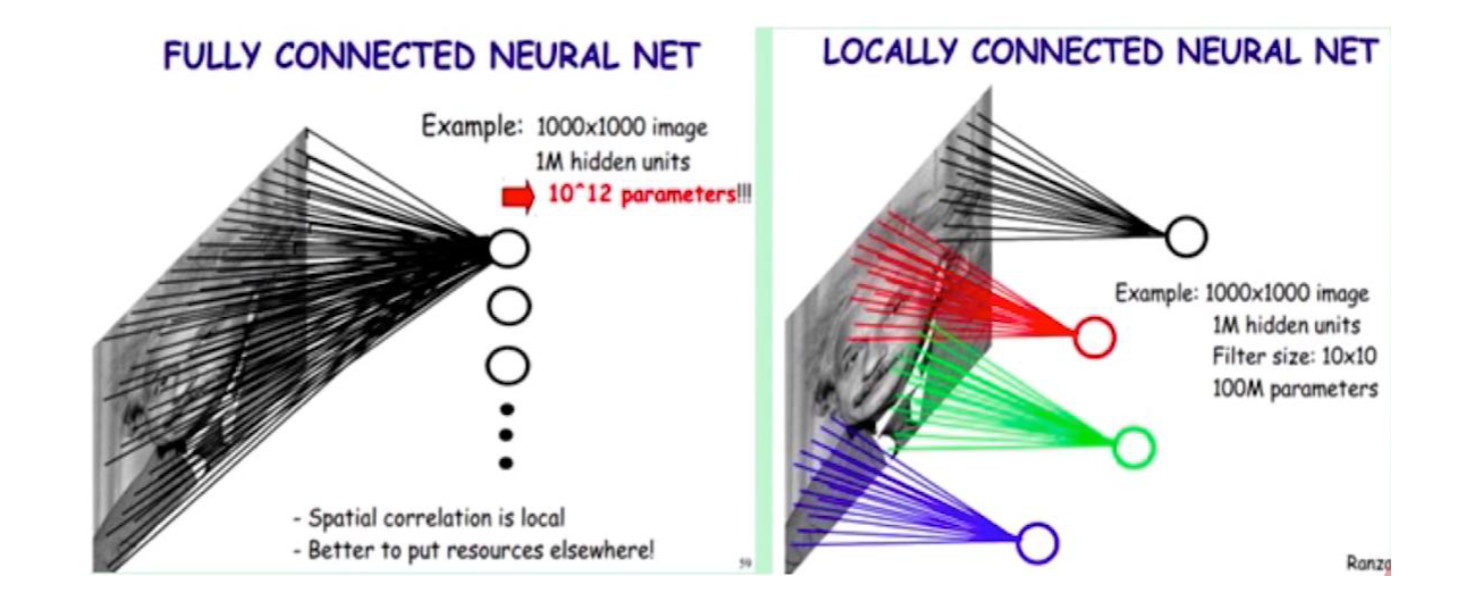
局部连接

局部连接举例：
图像大小 1000×1000，下一层神经元为 10^6，局部连接范围为 10×10，也就是只跟图像中的 100 个像素做连接，全连接参数为 10*10*10^6 = 10^8 .

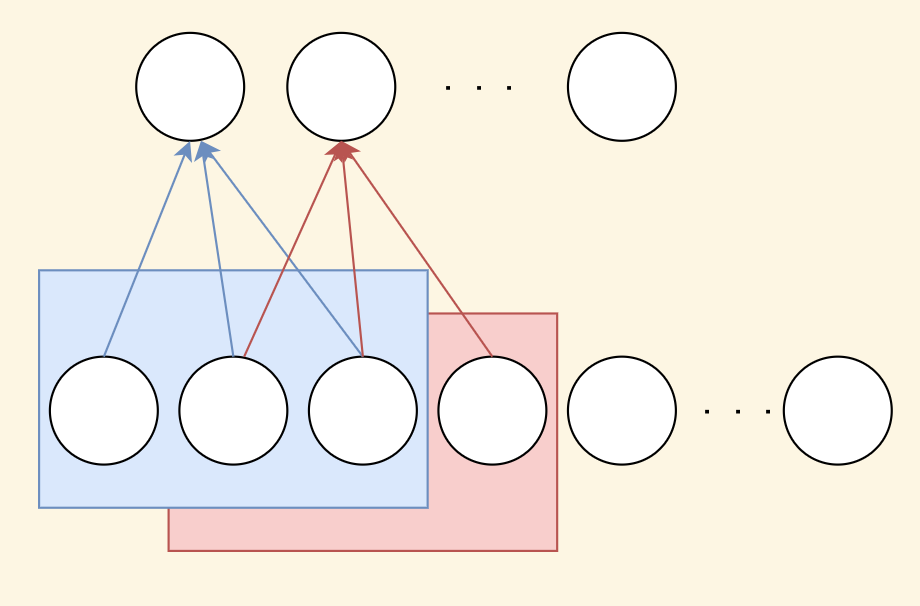
上图反而不太好理解？我这里画一个个人的理解（仅粗糙的原理示意）：

为什么可以这么做？
局部连接：图像的区域性，爱因斯坦的嘴唇附近的色彩是相似的。

10^8 依然是很多的！

卷积操作、参数共享

如何做卷积？把卷积核和它相对应部分做乘法，然后再求和。

这时我们得到启发，我们将一张图片通过某种映射关系压缩了（尽管这种压缩对于人眼来说可能是无意义的）。我们得到减少训练参数的思路。

input: 一张图片，output: 经过卷积操作后缩小的图片。
我们只需要调整卷积核里面的参数，这里面的参数是需要学习的。

为什么可以这么做？
参数共享与平移不变性：图像特征与位置无关。左边是脸，右边也是脸，这样无论脸放在什么地方都检查出来，刚好可以解决过拟合的问题（否则脸放到其他地方就检测不出来）。
更多、更详细的参考：https://github.com/dropsong/dl-ipynb-examples/blob/master/%E5%8D%B7%E7%A7%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/%E5%8D%B7%E7%A7%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9CCNN%E7%9A%84%E7%94%B1%E6%9D%A5%EF%BC%8C%E4%B8%BA%E4%BB%80%E4%B9%88%E8%A6%81%E7%94%A8%E5%8D%B7%E7%A7%AF%EF%BC%9F_%E5%8D%B7%E7%A7%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C%E4%B8%BA%E4%BB%80%E4%B9%88%E5%8F%AB%E5%8D%B7%E7%A7%AF-CSDN%E5%8D%9A%E5%AE%A2.pdf

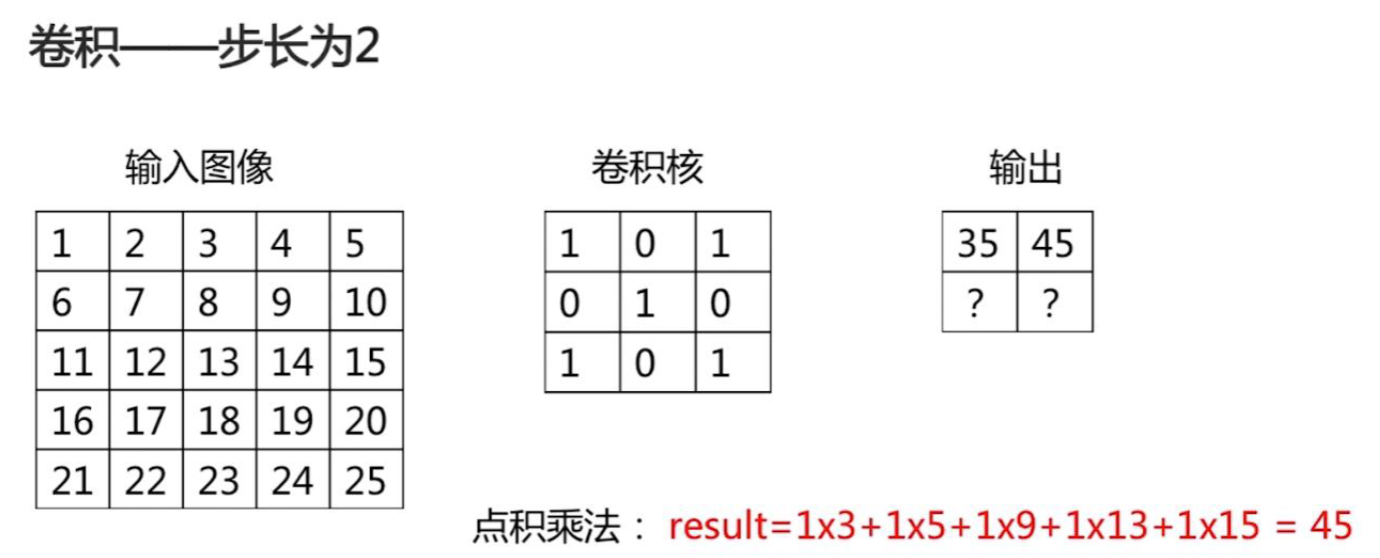
考虑卷积操作的步长：

输出图像尺寸 = 1+(n-k)//s, s 是步长。

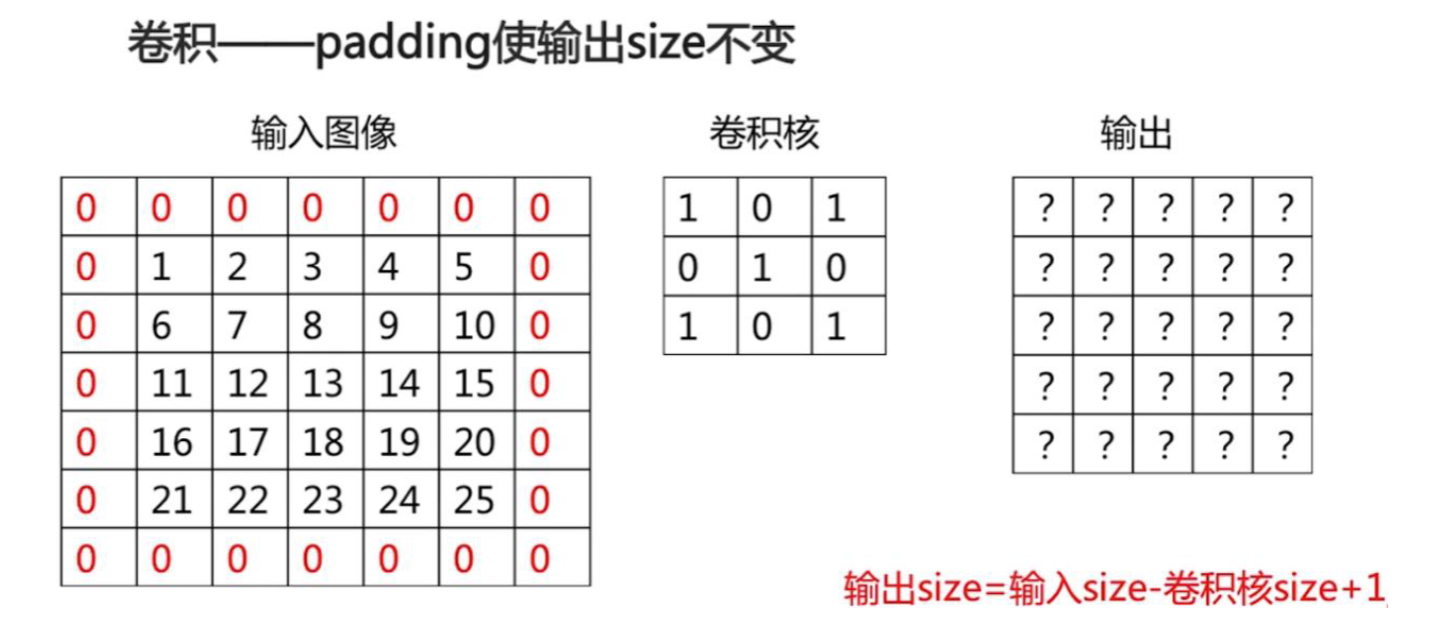
新的问题：步长变大，输出变小，那最后导致图像没了怎么办？或者在一些边界上怎么处理？
采用如下 padding 手法：

池化

池化函数使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出。本质是降采样，可以大幅减少网络的参数量。

池化技术的本质：在尽可能保留图片空间信息的前提下，降低图片尺寸，提取高层特征，同时减少网络参数量，预防过拟合。图片的主体内容丢失不多，依然具有平移，旋转，尺度的不变性，简单来说就是图片的主体内容依旧保存着原来大部分的空间信息。

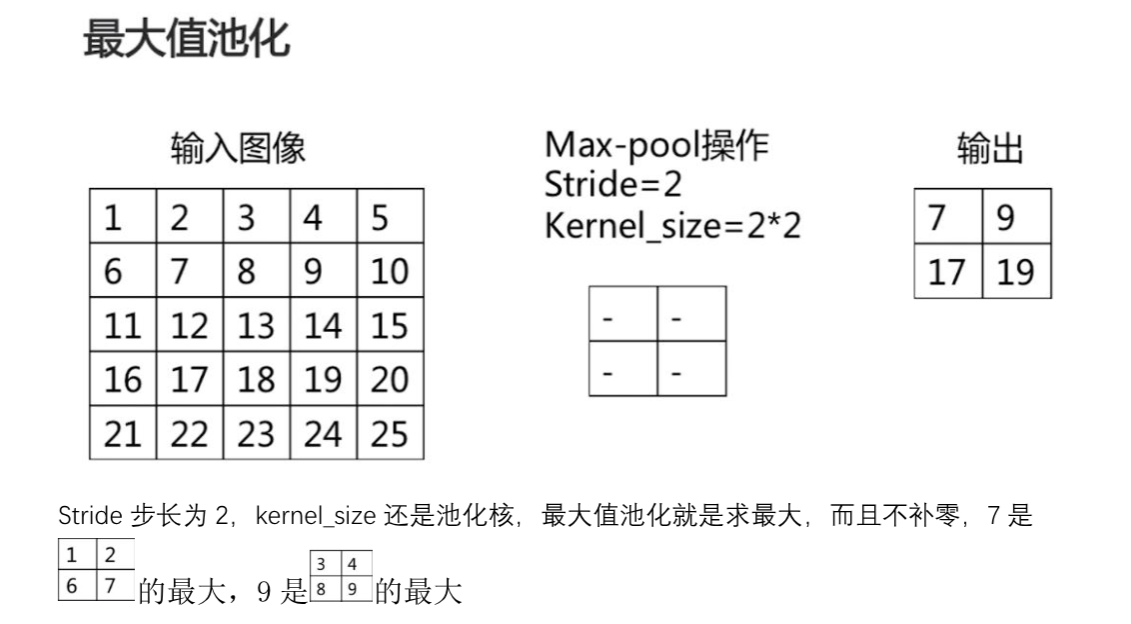
最大值池化，能够抑制网络参数误差造成的估计均值偏移的现象。

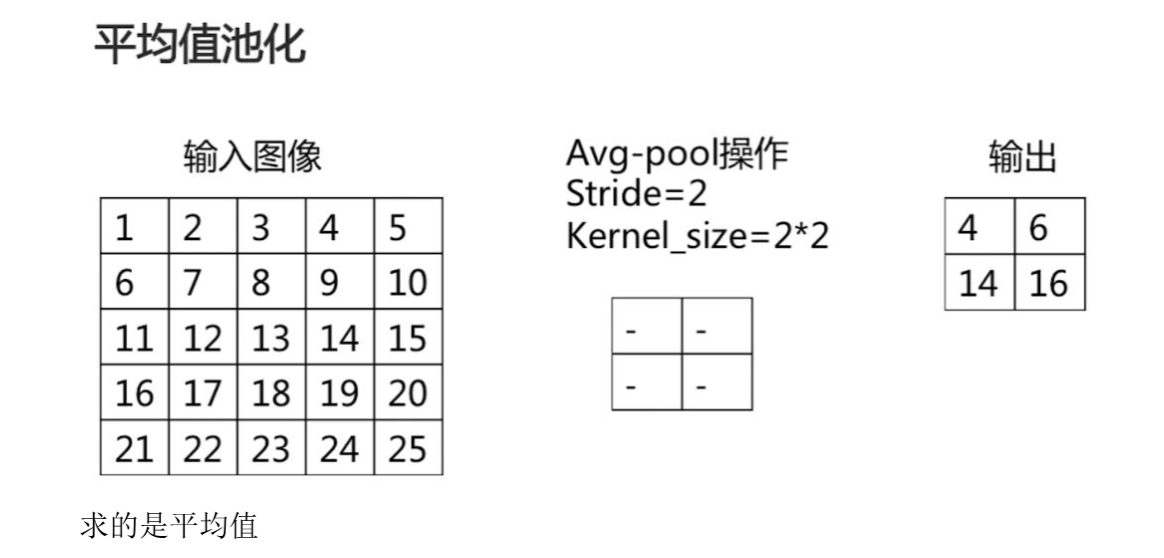
平均值池化，主要用来抑制邻域值之间差别过大，造成的方差过大。

池化操作特点：

常使用不重叠、不补零的方式
没有用于求导的参数（没有需要训练的参数，参数个数为 0）
池化层的超参数为步长和池化核大小
减少图像尺寸，从而减少计算量
一定程度平移鲁棒
- 比如一只猫移动了一个像素的另外一张图片，我们先做池化，再做卷积，那么最终还是可以识别这个猫
损失了空间位置精度

实战

本 notebook 包含以下内容：

fashion_mnist 数据集上使用卷积神经网络
多通道的图片如何卷积
使用多个卷积核
搭建卷积神经网络的经典流程
卷积神经网络的参数量计算

本 notebook 包含以下内容：

在上一个的基础上改变了激活函数

本 notebook 包含以下内容：

深度可分离卷积
深度可分离卷积的参数量计算、优化比例

本 notebook 、notebook 包含的内容：

10-monkeys 数据集
图片增强
卷积神经网络进行图像分类

迁移学习

迁移学习在研究领域上属于机器学习。它专注于存储已有问题的解决模型，并将其利用在其他不同但相关的问题上。比如说，用来辨识汽车的知识（或者是模型）也可以被用来提升识别卡车的能力。计算机领域的迁移学习和心理学常常提到的学习迁移在概念上有一定关系，但是两个领域在学术上的关系非常有限。

迁移学习的领域很大，它不是深度学习的一个子领域，而是与深度学习有交叉的领域。一般来说，迁移学习包括基于样本的迁移，基于特征的迁移，基于模型的迁移，以及基于关系的迁移。

迁移学习按照学习方式可以分为基于样本的迁移，基于特征的迁移，基于模型的迁移，以及基于关系的迁移。基于样本的迁移通过对源域中有标定样本的加权利用完成知识迁移；基于特征的迁移通过将源域和目标域映射到相同的空间（或者将其中之一映射到另一个的空间中）并最小化源域和目标域的距离来完成知识迁移；基于模型的迁移将源域和目标域的模型与样本结合起来调整模型的参数；基于关系的迁移则通过在源域中学习概念之间的关系，然后将其类比到目标域中，完成知识的迁移。

ResNet

基本知识

ResNet 是 2015 年何凯明、张翔宇、任少卿、孙剑共同提出的。

使用更深层的网络时，会发生梯度消失、梯度爆炸的问题，这个问题可以通过标准的初始化和正则化层基本解决，这样可以确保几十层的网络仍能够收敛。但是随着网络层数的增加，梯度消失或者爆炸的问题依旧存在。

还有一个问题就是网络的退化，举个例子，假设已经有了一个最优化的网络结构，是 18 层。当我们设计网络结构的时候，我们并不知道具体多少层的网络是最优结构，假设我们设计了 34 层网络结构，那么多出来的 16 层其实是冗余的，我们希望训练网络的过程中，模型能够自己训练它们为恒等映射，也就是经过这层时的输入与输出完全一样。但是模型往往很难正确地将这 16 层学习为恒等映射，那么最终得到的效果就会比最优的 18 层网络结构差。这就是网络深度增加时，模型产生退化的现象。它不是由过拟合产生的，而是由冗余的网络层学习了不是恒等映射的参数造成的。

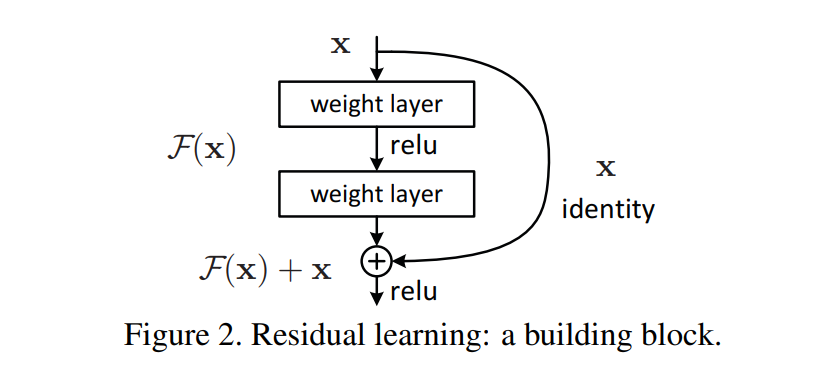
具体哪些层是恒等层，这个由网络训练时自己判断。将原网络的几层改成一个残差块，残差块的具体构造如下图所示：

在第二层输出值激活前加入 X，这条路径称作 shortcut 连接。

我们发现，假设该层是冗余的，在引入 ResNet 之前，我们想让该层学习到的参数能够满足 h(x)=x，即输入是 x，经过该冗余层后，输出仍然为 x. 但是要想学习 h(x)=x 恒等映射时的这层参数比较困难。ResNet 想到避免去学习该层恒等映射的参数，使用了如上图的结构，让 h(x)=F(x)+x; 这里的 F(x) 称作残差项，我们发现，要想让该冗余层能够恒等映射，只需要学习 F(x)=0. 学习 F(x)=0 比学习 h(x)=x 要简单，因为一般每层网络中的参数初始化偏向于 0，这样在相比于更新该网络层的参数来学习 h(x)=x，该冗余层学习 F(x)=0 的更新参数能够更快收敛。

实战

本 notebook 包含的内容：

使用 10-monkeys 数据集
微调 resnet，做图像分类

卷积神经网络进阶

本 notebook 包含以下内容：

在 kaggle 上打比赛的大致流程
CIFAR-10 - Object Recognition in Images
在 kaggle 上进行更复杂的输入输出文件操作
使用卷积神经网络

模型演变：AlexNet、VGG、ResNet、Inception、MobileNet.

为什么要讲不同的网络结构？

不同的网络结构解决的问题不同
不同的网络结构使用的技巧不同
不同的网络结构应用的场景不同

模型的进化：

更深更宽： AlexNet 到 VGGNet
不同的模型结构： VGG 到 InceptionNet/ResNet
优势组合： Inception+Res = InceptionResNet
自我学习： NASNet
实用： MobileNet

AlexNet

请参考：

VGGNet

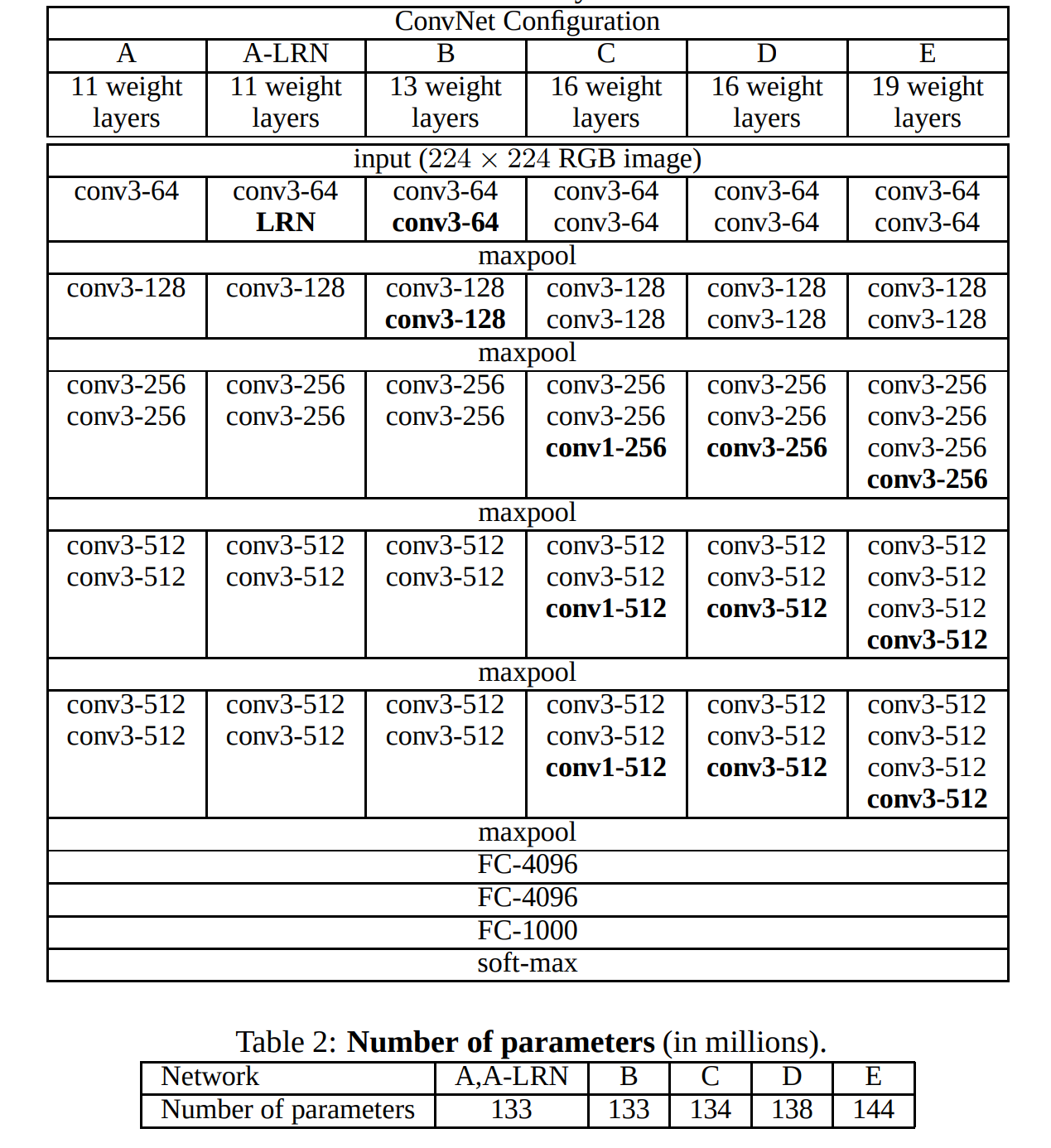
ImageNet 2014，分类第二，物体检测第一。论文地址：https://arxiv.org/abs/1409.1556

网络结构层次更深
多使用 3x3 的卷积核
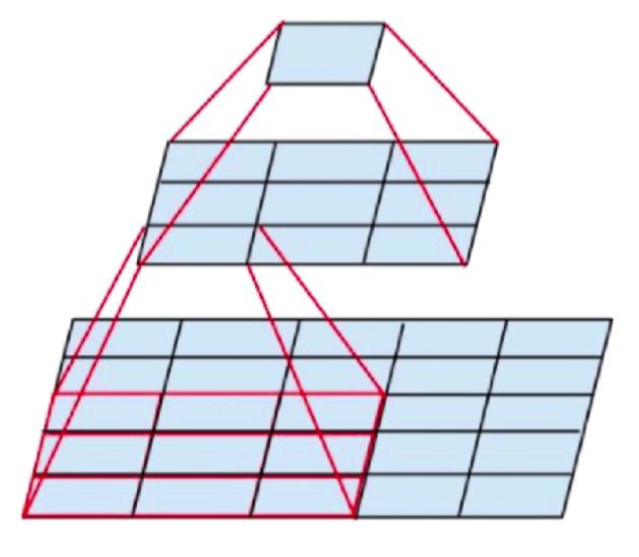
- 2 个 3x3 的卷积层可以看做一层 5x5 的卷积层，见图 106-20
- 3 个 3x3 的卷积层可以看做一层 7x7 的卷积层
- 1x1 的卷积层可以看做是非线性变换
每经过一个 pooling 层，通道数目翻倍

视野域：2 个 3x3 = 1 个 5x5，但是为什么要这样做呢？

2 层比 1 层多一次非线性变换
参数降低 28%， 5*5-3*3-3*3=7, 7/25=28%，参数量降低 28% .

训练技巧：

LRN 是局部做归一化
为什么都在后面加层？因为前面经过 maxpooling 后，后面参数没那么多，加层的计算量没那么大
先训练浅层网络如 A，再去训练深层网络多尺度输入
不同的尺度训练多个分类器，然后做 ensemble 随机使用不同的尺度缩放然后输入进分类器进行训练

本 notebook 包含以下内容：

tensorflow 1 的一些使用（过时）
模仿 vgg 的实现

ResNet

可以参考前面的部分，有这个小标题是为了展示卷积神经网络的发展历史，这里仅放一个 ipynb 文件。

本 notebook 包含的内容：

使用过时的 tensorflow 1 版本
实现 ResNet 的大致思路

InceptionNet

GoogLeNet/Inception v1 架构论文： https://arxiv.org/abs/1409.4842

InceptionNet 可以看作是一种工程优化，同样的参数量更有效率。

分组卷积：

可以参考的内容（机翻注意⚠️）：

InceptionNet v2 和 InceptionNet v3 在同一篇论文中提出：
https://arxiv.org/abs/1512.00567v3

这个版本提出了许多升级，这些升级提高了准确性并降低了计算复杂度。

3x3 不是最小卷积核，3x3 效果类似于 1x3 加上 3x1，这样比较极致，减少 33% .

Inception-v4, 论文地址：
https://arxiv.org/abs/1602.07261

本 notebook 包含的内容：

使用过时的 tensorflow 1
实现 inception net 的大致思路

MobileNet

MobileNet is a family of convolutional neural network (CNN) architectures designed for efficient image classification, object detection, and other computer vision tasks on mobile and embedded devices. They are known for their small size, low latency, and low power consumption, making them suitable for resource-constrained environments.

论文地址： https://arxiv.org/abs/1704.04861

参考文章：

本 notebook 包含的内容：

使用过时的 tensorflow 1 代码
自行编写深度可分离卷积
实现 MobileNet 的大致思路

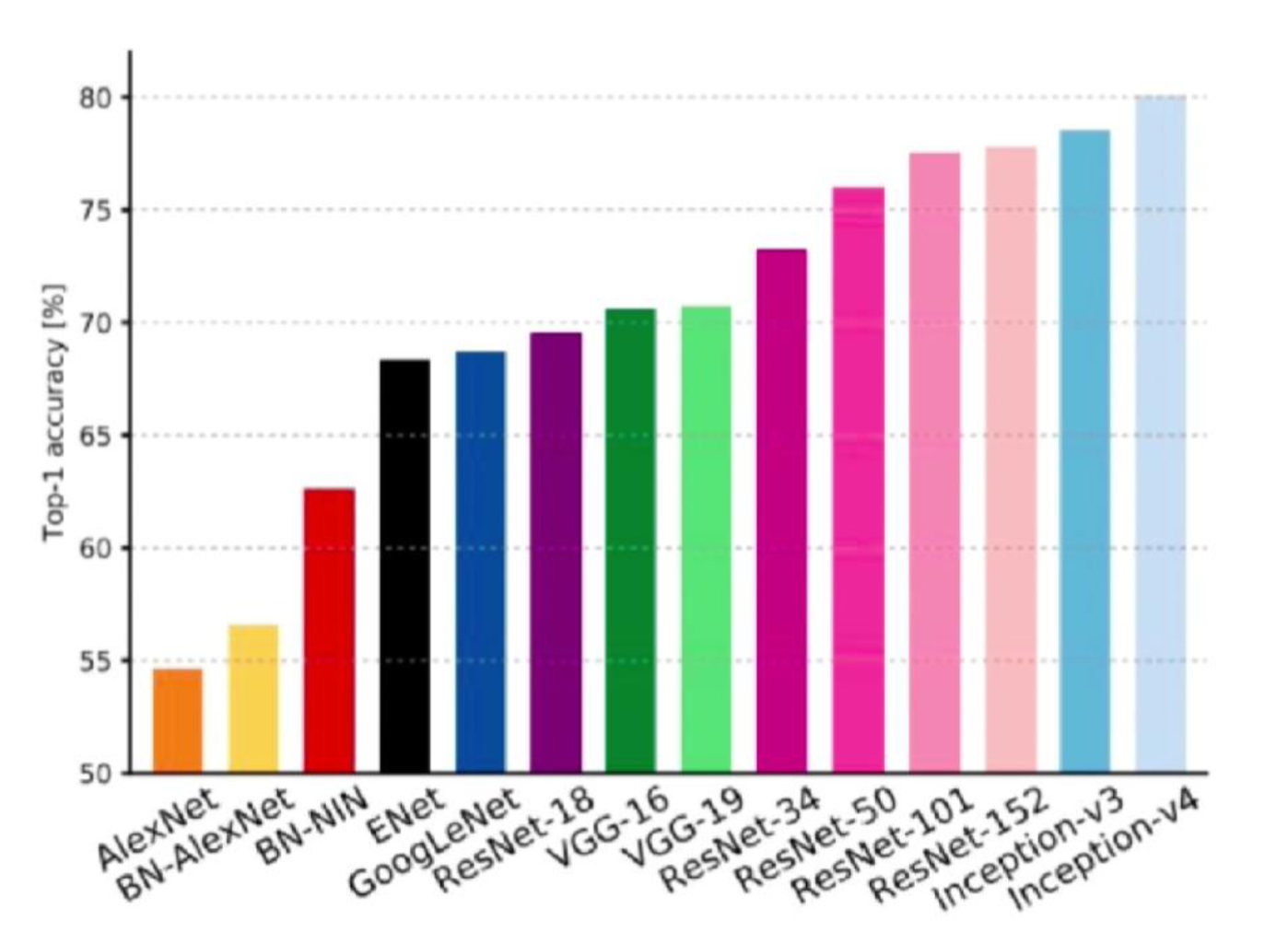
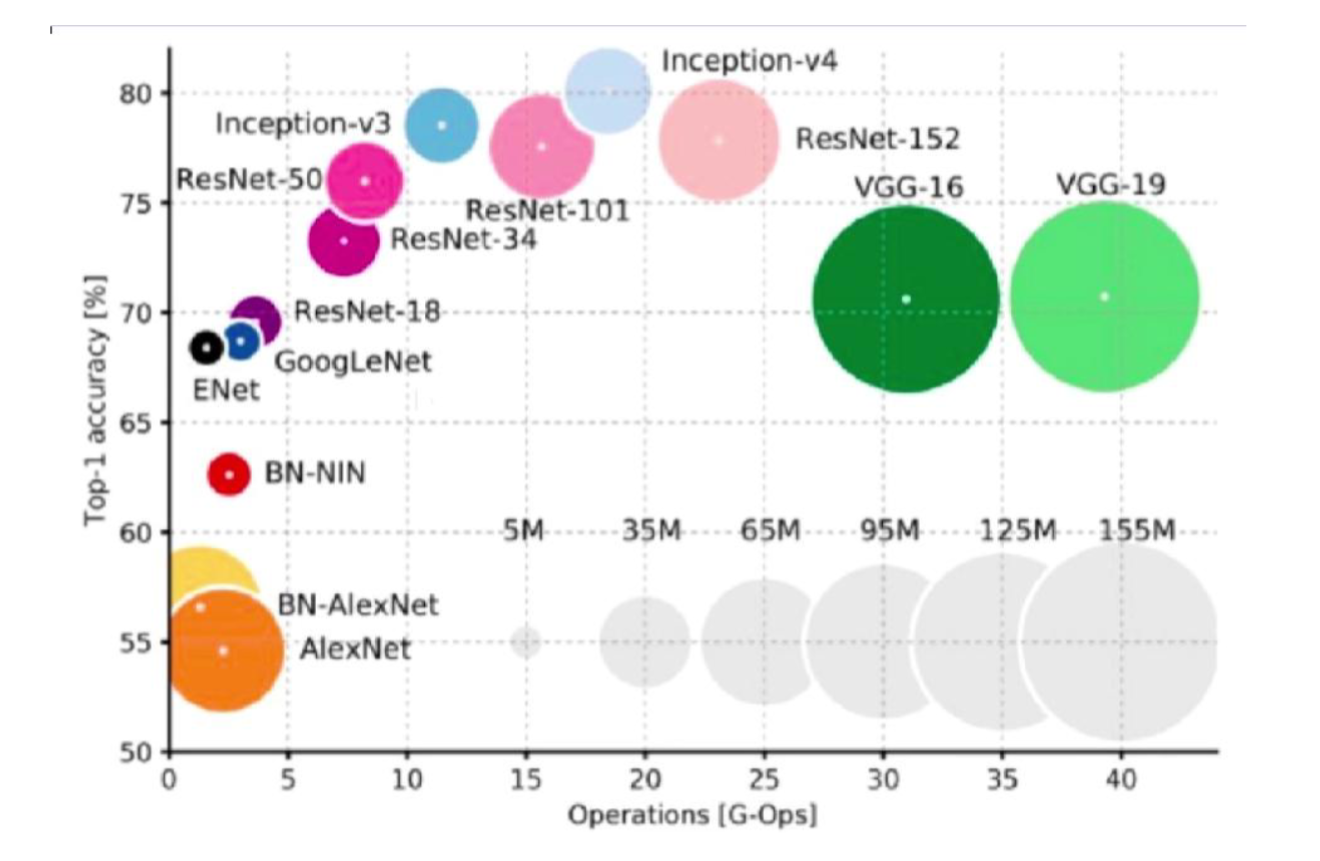
不同模型结构的对比

此外，还有 NASNet，是强化学习，并不在图中。

效果计算量分析（性价比）。横轴是计算量，纵轴是精确率，圆圈大小是模型参数量的多少，可以看到 V3 非常的不错：

卷积神经网络调参

不同的优化器

对于稀疏数据，使用学习率可自适应方法。

SGD 通常训练时间更长，最终效果比较好，但需要好的初始化和 learning rate。

需要训练较深较复杂的网络且需要快速收敛时，推荐使用 adam. 设定一个比较小的 learning rate 值。

Adagrad, RMSprop, Adam 是比较相近的算法，在相似的情况下表现差不多。

前情提要 - 梯度下降

随机梯度下降的问题：

局部极值
Saddle point 问题（鞍点问题）

动量（momentum）梯度下降，通过一个比喻来理解：

想象一个从山坡上滚下来的小球。在普通的梯度下降中，小球的每一步只取决于当前位置的坡度。而带有动量的小球，则会积累滚动的速度。当它冲下陡坡时，会越滚越快；即使遇到比较平缓的区域，由于“惯性”的存在，它也会继续前行一段距离，而不是立即停下。

在标准的梯度下降中，参数 $w$ 的更新仅仅依赖于当前位置的梯度 $\nabla J(w)$ 和学习率 $\eta$。更新的向量可以表示为 $\Delta w_t$：

$\Delta w_t = -\eta \cdot \nabla J(w_t)$

参数更新规则为：

$w_{t+1} = w_t + \Delta w_t = w_t - \eta \cdot \nabla J(w_t)$

动量法引入了一个“速度”向量 $v$ (velocity)，它会累积历史的梯度信息。参数更新分为两步：

首先，计算当前的速度 $v_t$。它由上一时刻的速度 $v_{t-1}$ (按动量因子 $\gamma$ 衰减) 和 当前梯度 共同决定：

$v_t = \gamma \cdot v_{t-1} + \eta \cdot \nabla J(w_t)$

然后，使用这个速度 $v_t$ 来更新参数：

$w_{t+1} = w_t - v_t$

$\gamma$ 是动量因子 (momentum)，一个介于 [0, 1] 之间的超参数，通常取值为 0.9 左右。它决定了历史速度的保留程度。
当梯度方向连续保持一致时，速度 $v_t$ 会持续累加，从而在那个方向上加速前进。
当梯度方向发生振荡时，历史速度可以抵消一部分相反的梯度，从而对更新路径起到平滑作用，实现减速和调整方向。

动量法通过累积历史梯度，带来了两个显著的优势：

加速收敛 (Accelerated Convergence)
- 在损失曲面中平坦但有持续梯度的方向（好比一个长长的缓坡峡谷），动量项会累积梯度，使得参数更新的步长越来越大，从而更快地穿越这些区域，整体上加速收敛。
提高精度与稳定性 (Improved Precision and Stability)
- 该优势主要体现在减少振荡。在损失曲面陡峭但梯度方向来回摆动的方向（好比峡谷的两壁），当前梯度与历史速度方向可能相反。动量项可以起到平滑和抑制作用，有效衰减这种振荡，使得更新方向更稳定地指向最优解。

AdaGrad

调整学习率，学习率随着训练次数的增加越来越小。

$n_t = n_{t-1} + g_t^2$

以往梯度的平方和作为分母，每次计算要除以它：

$\Delta \theta_t = - \frac{\eta}{\sqrt{n_t+ \epsilon}} \cdot g_t$

伪代码：

grad_squared = 0
while True:
  dx = compute_gradient(x)
  grad_squared += dx * dx
  x -= learning_rate * dx / (np.sqrt(grad_squared) + 1e-7)

前期，regularizer 较小，放大梯度；后期，regularizer（分母）较大，缩小梯度。梯度随训练次数降低。

AdaGrad 算法缺点：

学习率设置太大，导致 regularizer（分母）影响过于敏感
后期，regularizer 累积值太大，提前结束训练

RMSProp

Adagrad 的变种，作了一些调整，由累积平方梯度变为平均平方梯度：

grad_squared = 0
while True:
  dx = compute_gradient(x)
  grad_squared = decay_rate * grad_squared + (1-decay_rate) * dx * dx
  x -= learning_rate * dx / (np.sqrt(grad_squared) + 1e-7)

解决了后期提前结束的问题。

Adam

伪代码：

first_moment = 0
second_moment = 0
while True:
  dx = compute_gradient(x)
  first_moment = beta1 * first_moment + (1-beta1) * dx  # Momentum
  second_moment = beta2 * second_moment + (1-beta2) * dx * dx  # Adagrad
  x -= learning_rate * first_moment / (np.sqrt(second_moment)+1e-7)

又加入了一个校准，校准的目的是一开始时，让 first_moment 和 second_moment 都变的稍微大一些：

first_moment = 0
second_moment = 0
for t in range(1, num_iterations):
  dx = compute_gradient(x)
  first_moment = beta1 * first_moment + (1-beta1) * dx
  second_moment = beta2 * second_moment + (1-beta2) * dx * dx
  first_unbias = first_moment / (1-beta1**t)
  second_unbias = second_moment / (1-beta2**t)
  x -= learning_rate * first_unbias / (np.sqrt(second_unbias)+1e-7)

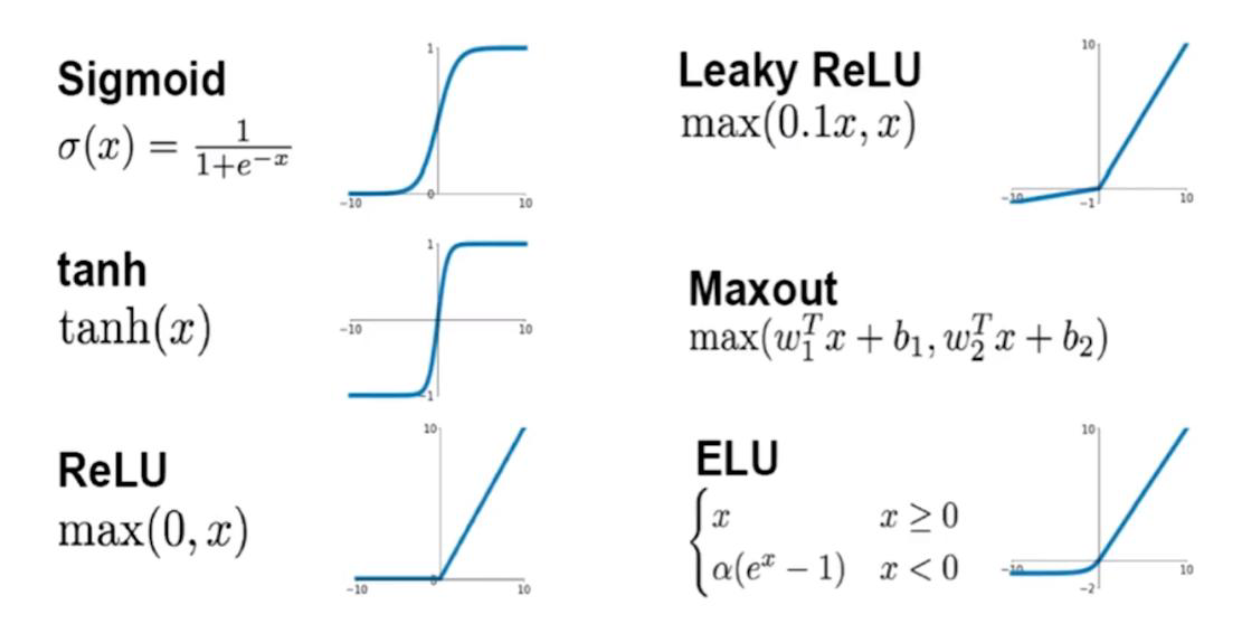
激活函数

Sigmoid

参考之前的内容。

Tanh

输入非常大或非常小时没有梯度
输出均值是 0: 相对于 sigmoid 的好处
计算复杂

ReLU

优点：

使用 ReLU 的 SGD 算法的收敛速度比 sigmoid 和 tanh 快。
在 x>0 区域上，不会出现梯度饱和、梯度消失的问题。
计算复杂度低，不需要进行指数运算，只要一个阈值就可以得到激活值。

缺点：

ReLU 的输出不是 0 均值的。
Dead ReLU Problem(神经元坏死现象)：ReLU 在负数区域被 kill 的现象叫做 dead relu. ReLU 在训练的时很“脆弱”。在 x<0 时，梯度为 0. 这个神经元及之后的神经元梯度永远为 0，不再对任何数据有所响应，导致相应参数永远不会被更新。

一个非常大的梯度流过神经元，不会再对数据有激活现象了，“很大的梯度流过神经元”的意思就是指：该神经元相关的参数被梯度下降算法更新了一次。
比如原来的参数可能是：[-10, 5, 7], 然后突然来了一个梯度是[-100, -100, -100], 这样参数就更新成了 [-110, -95, -93]。然后如果接下来的收到的数据都是[a, b, c], 其中 a, b, c >=0, 这个时候神经元的输出恒为 0，于是不会再有梯度传回来。因而参数得不到更新，也就变成了 dead cell 了。

产生这种现象的原因：

参数初始化问题
learning rate 太高导致在训练过程中参数更新太大

解决方法：
采用 Xavier 初始化方法，以及避免将 learning rate 设置太大或使用 adagrad 等自动调节 learning rate 的算法。

Leaky-ReLU

Leaky ReLU is an activation function in neural networks that addresses the “dying ReLU” problem by allowing a small, non-zero gradient for negative inputs, unlike the standard ReLU which outputs zero. This helps prevent neurons from becoming completely inactive during training, especially in deep networks.

$\text{LeakyReLU}(x) = \begin{cases} x, & x>0 \\ \alpha x, & x \le 0 \end{cases}$

其中，$ \alpha $ 通常取值 0.01 ，Leaky-ReLU 的函数范围是 $(-\infty, +\infty)$ .

ELU

具有 relu 的优势，没有 Dead ReLU 问题，输出均值接近 0，实际上 PReLU 和 Leaky ReLU 都有这一优点。有负数饱和区域，从而对噪声有一些鲁棒性。 可以看做是介于 ReLU 和 LeakyReLU 之间的一个函数。当然，这个函数小于零时也需要计算 exp，从而计算量更大。

Maxout

$\text{max}(w_1^T x + b_1, w_2^T x + b_2)$

没有 dead relu 问题。参数翻倍。

优点：

Maxout 的拟合能力非常强，可以拟合任意的凸函数
Maxout 具有 ReLU 的所有优点，线性、不饱和性
不会出现神经元坏死的现象

缺点：
增加了太多参数量。maxout 还需要反向传播去更新它自身的权重系数。

总结

Relu, 小心设置 learning rate（初始值不要太大）
不要使用 sigmoid（relu 出现后，就不用它了，收敛太慢）
使用 LeakyRelu、maxout、ELU
可以试试 tanh，但不要抱太大期望（因为计算量大）

网络初始化（w和b）

有关论文： Understanding the difficulty of training deep feedforward neural networks .

论文解析： https://zhuanlan.zhihu.com/p/43840797

如何分析初始化结果好不好？

查看初始化后各层的激活值分布，激活值就是经过激活函数后的值，如果分布是固定的在 -1到 1，或者 0 到 1 之间，那没问题，如果集中在某一个值，那就不太好。

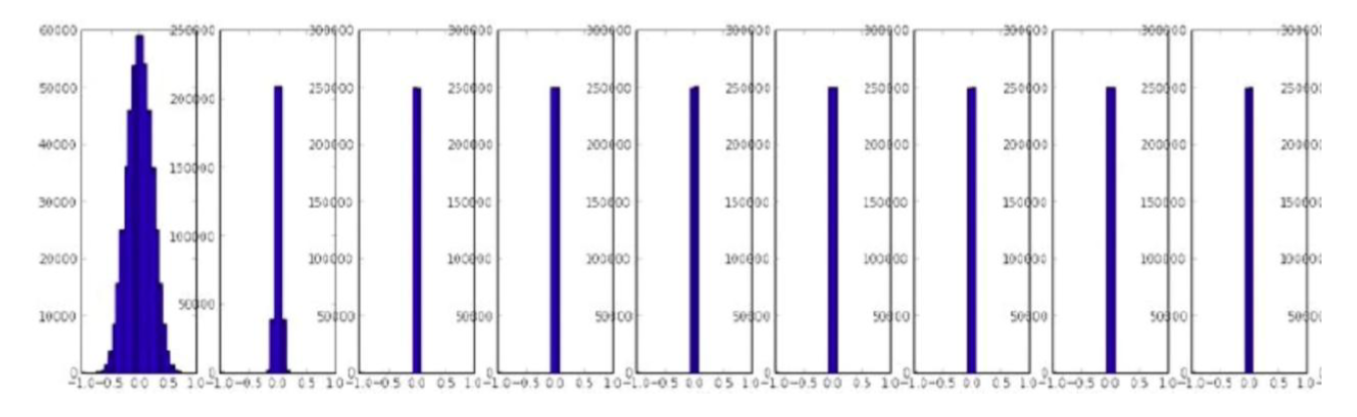
用均值为 0，方差为 0.02 的正态分布初始化（tanh），如下图所示（依次往后看是经过每一层后的效果），高层均值为 0，没有梯度：

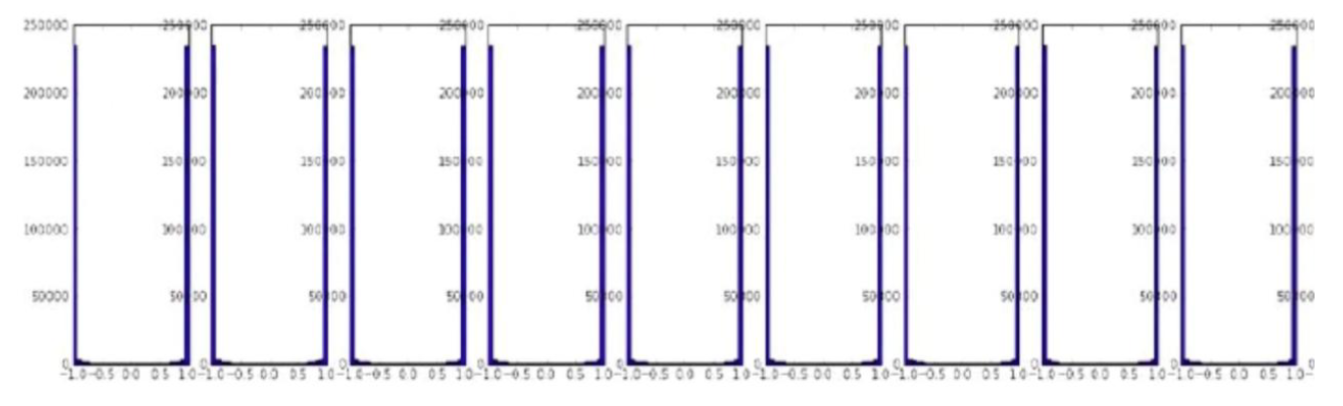
用均值为 0，方差为 1 的正态分布初始化（tanh），如下图所示，高层均值为-1,1，已经饱和：

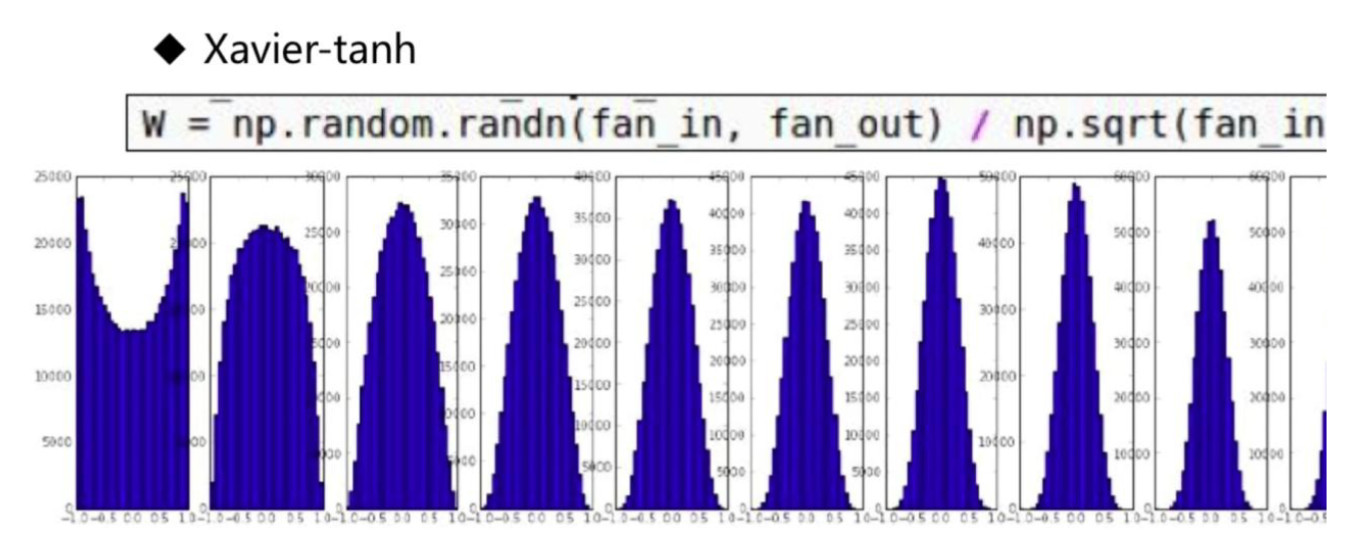
Xavier 分布（glorot_uniform） 在 tanh 上表现很好：

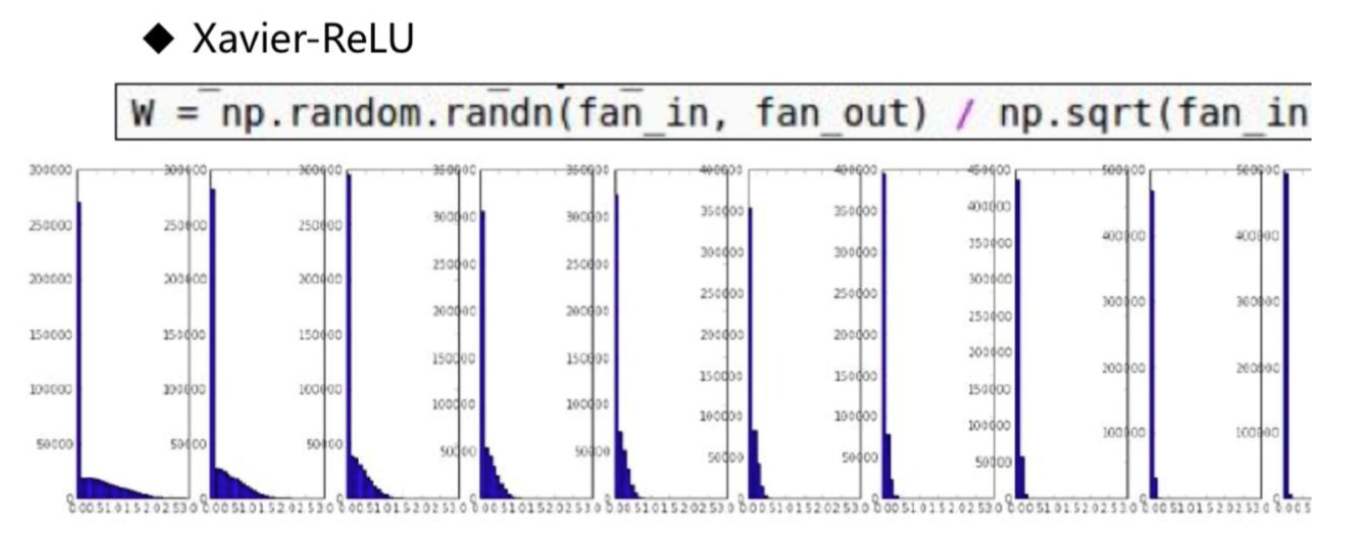
Xavier 分布在 ReLU 上表现并不好：

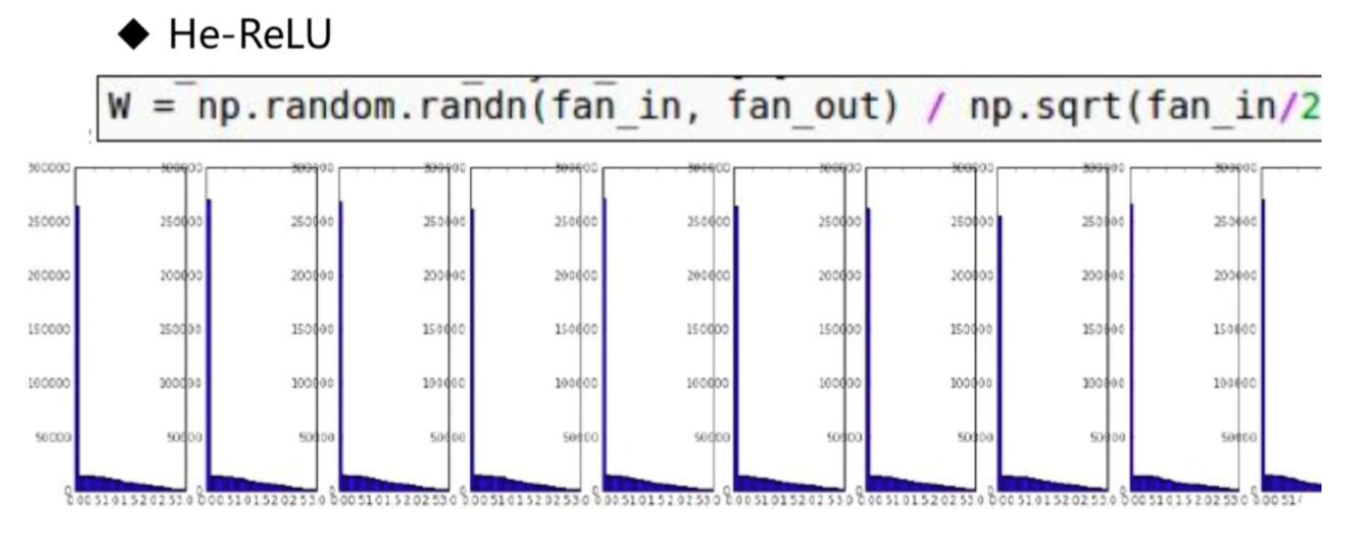
何凯明发明了 He Initialization，对 ReLU 效果较好：

关于 He Initialization，可参考：

Mastering Weight Initialization in Neural Networks: A Beginner’s Guide
PyTorch documentation - torch.nn.init ，网页搜索 kaiming

批归一化

参照之前。

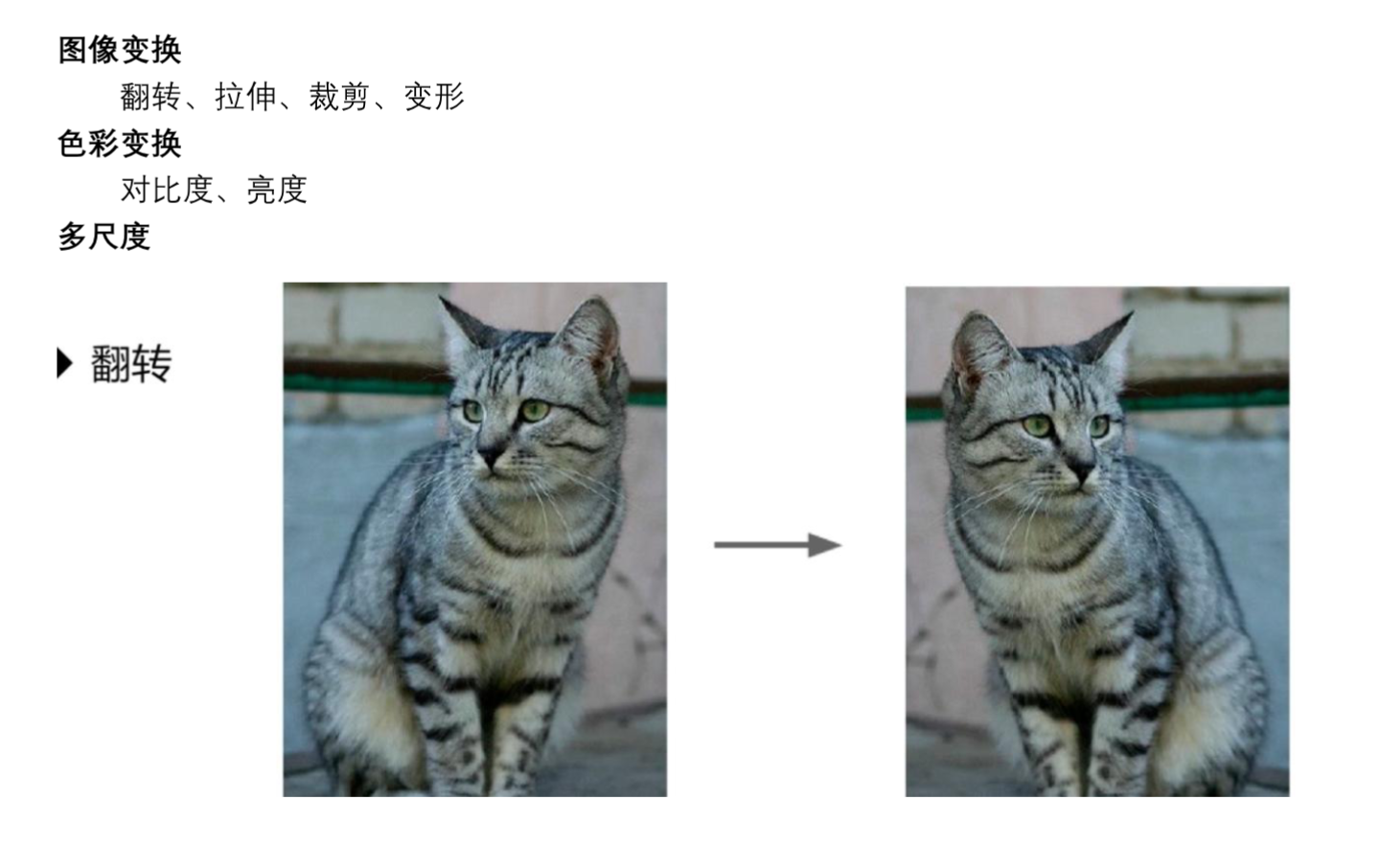
数据增强

实战

本 notebook 包含的内容：

使用 tensorflow 1 的 tensorboard

本 notebook 包含的内容：

使用老旧的 tensorflow 1
加载、保存模型的方法
checkpoint

本 notebook 包含的内容：

老旧的 tensorflow 1 版本
尝试调整激活函数、初始化分布、优化器

本 notebook 包含的内容：

老旧的 tensorflow 1 版本
图像增强

本 notebook 包含的内容：

老旧的 tensorflow 1 版本
更深的网络深度

本 notebook 包含的内容：

老旧的 tensorflow 1 版本
卷积搞为装饰器（类似），这样方便很多
批归一化

图像风格变换

神经网络可以做什么

图像风格转换：

106-34

图像修复（第三列是传统修复，第四列是深度学习修复）：

换脸（第二个是传统地 P 了一张脸上去，第三个是可以保证脸型和肤色还是原有的）：

还有图片超清化，图像生成文字等。

卷积神经网络学到了什么

参考论文： https://arxiv.org/abs/1311.2901

经验总结（一种尝试性质的解释）：

卷积神经网络的每一层的激活值都可以看做是图像的抽象表示
卷积神经网络中某层的每个激活值都可以看做是一个分类器，众多的分类结果组成了抽象表示
层级越高，特征抽象程度越高

图像风格转换（简单版本）

参考论文： https://arxiv.org/abs/1508.06576

发展历史：图像风格迁移(Neural Style)简史，内容已在 github 备份。

不可能存在一个风格变换的目标值，所以是一个无监督问题。

希望的效果：输出图像既和原图很相近，也和风格图片很相近。

根据之前的笔记内容 “卷积神经网络学到了什么”，对于原图，可以计算其内容特征；对于风格图片，可以计算其风格特征。

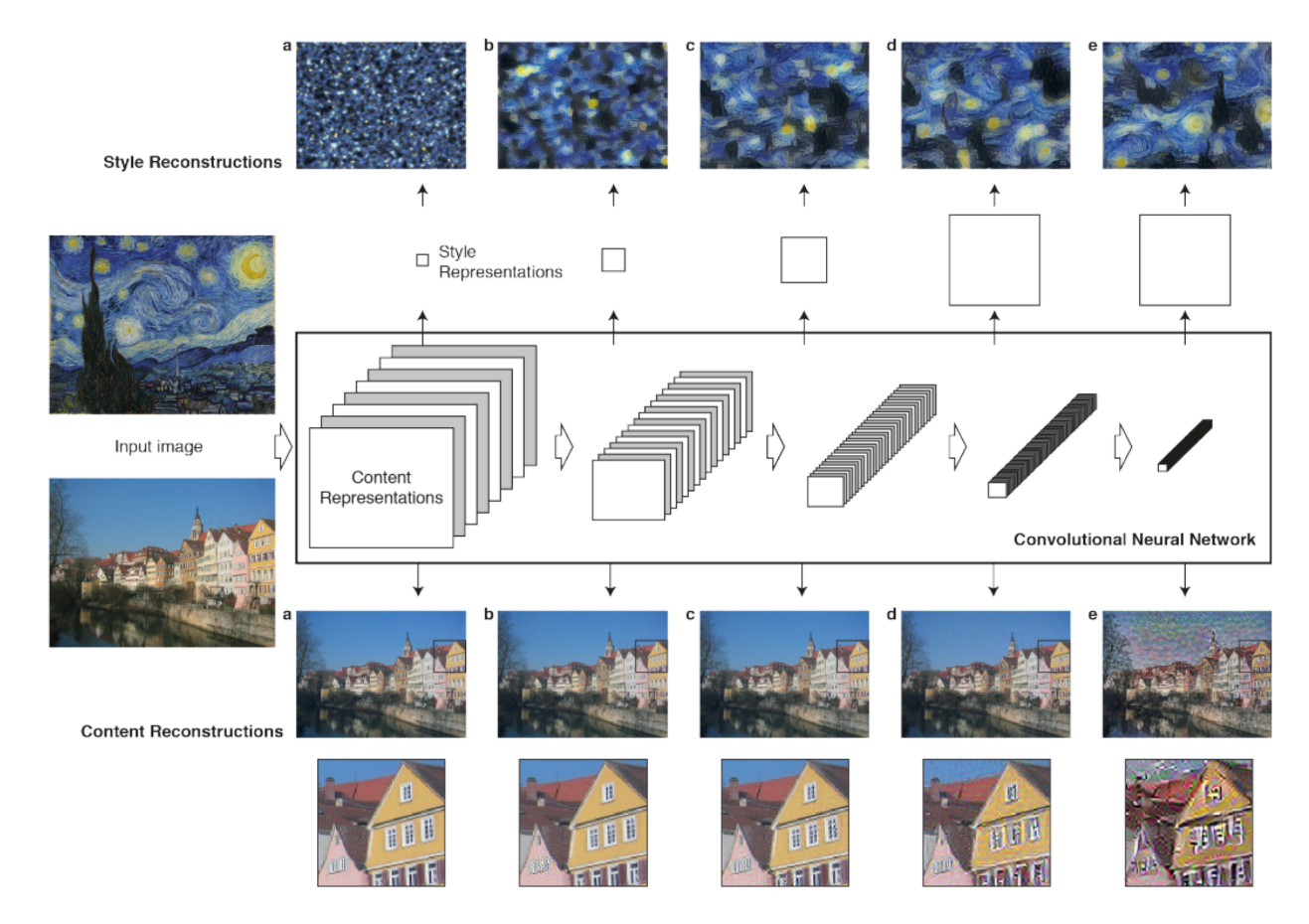
图片在 CNN 的不同处理阶段中表现出不同的 filtered images ：

重要性质：

Higher layers in the network capture the high-level content in terms of objects and their arrangement in the input image but do not constrain the exact pixel values of the reconstruction.
- the size and complexity of local image structures from the input image increases along the hierarchy, a result that can be explained by the increasing receptive field sizes and feature complexity.
In contrast, reconstructions from the lower layers simply reproduce the exact pixel values of the original image.

思路：虽然这是一个无监督的问题，但是为了达到“相近”，还是可以计算损失。

我们希望 内容损失+风格损失 是最小的（这里的 + 不一定是数值上简单的求和）。

所以要计算两个损失：

对内容图片的损失
对风格图片的损失

对于内容，关键思路：we perform gradient descent on a white noise image to find another image that matches the feature responses of the original image.

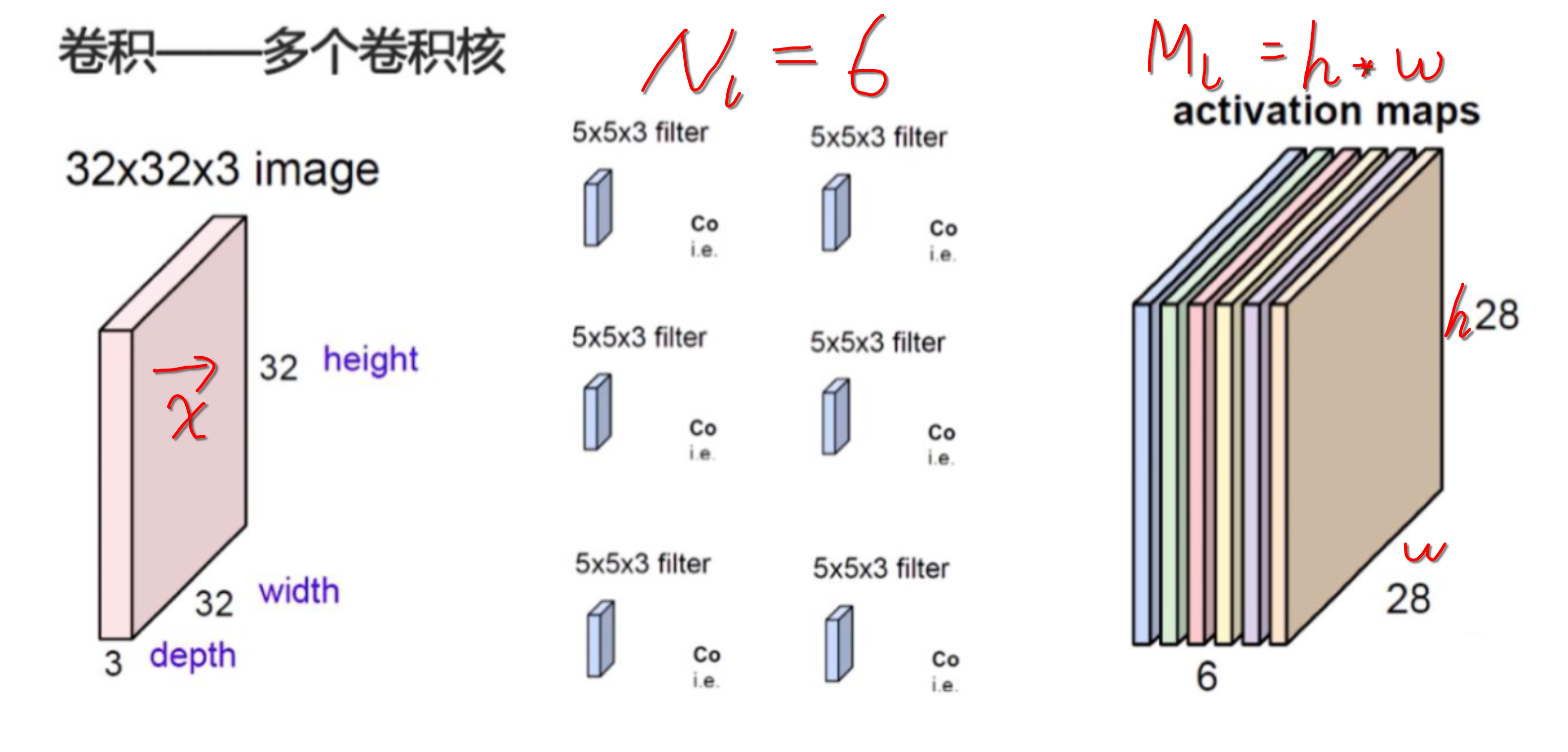
为方便起见，记：

因此 layer $l$ 的 responses 可以存储在矩阵 $F^l \in \cal{R}^{\it{N_l \times M_l}}$ 中，where $F^l_{ij}$ is the activation of the $i^{th}$ filter at position $j$ in layer $l$.

记原图为 $\vec{p}$ ，$P^l$ 是其在 layer $l$ 对应的 feature representation. 记待生成的图像为 $\vec{x}$，$F^l$ 是其在 layer $l$ 对应的 feature representation. 记损失：

$\cal{L}_{\it{content}} (\vec{p}, \vec{x}, l) = \frac{1}{2} \sum _{i,j} (\it{F^l_{ij}} - P^l_{ij})^2$

激活函数是 relu, 则

$\frac{\partial \cal{L}_{\it{content}}}{\partial F^l_{ij}} = \begin{cases} (F^l-P^l)_{ij} & \text{if }F^l_{ij} > 0 \\ 0 & \text{if } F^l_{ij} < 0 \end{cases}$

对于风格，On top of the CNN responses in each layer of the network we built a style representation that computes the correlations between the different filter responses, where the expectation is taken over the spatial extend of the input image.

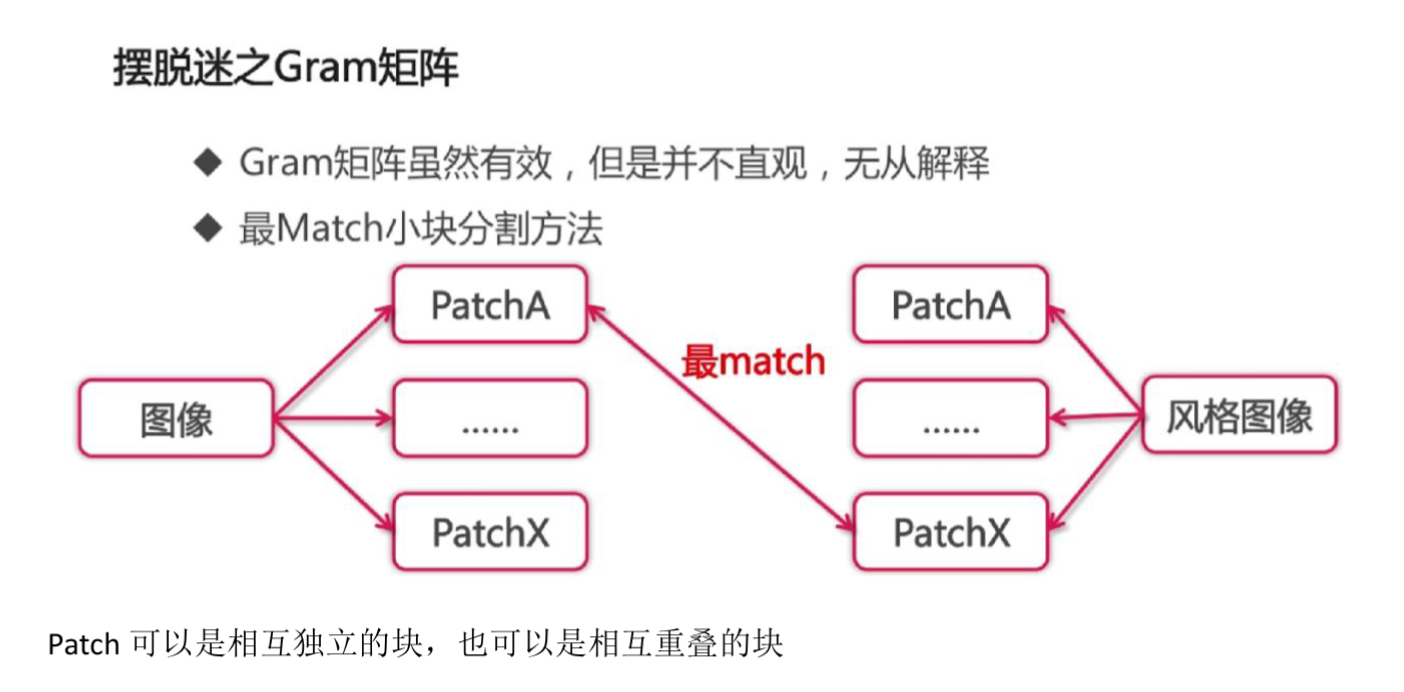
特征相关性由 Gram 矩阵 $G^l \in \cal{R}^{\it{N_l} \times N_l}$ 给出，$G^l$ 在第 $i$ 行第 $j$ 列的元素 $G^l_{ij}$ 为：

$G^l_{ij} = \sum_k F^l_{ik}F^l_{jk}$

$G^l_{ij}$ 是 layer $l$ 里，向量化的 feature map $i$ 和 $j$ 的内积。示意图如下：

因为这里的 feature map 是向量化的（类似于 tensorflow 中的展平操作），所以其实也可以有如下写法：

$G^l = F^l \cdot (F^l)^T$

这里同时得出之后会用到的重要性质：$G^l$ 是对称阵，也即 Gram 矩阵是对称阵 。

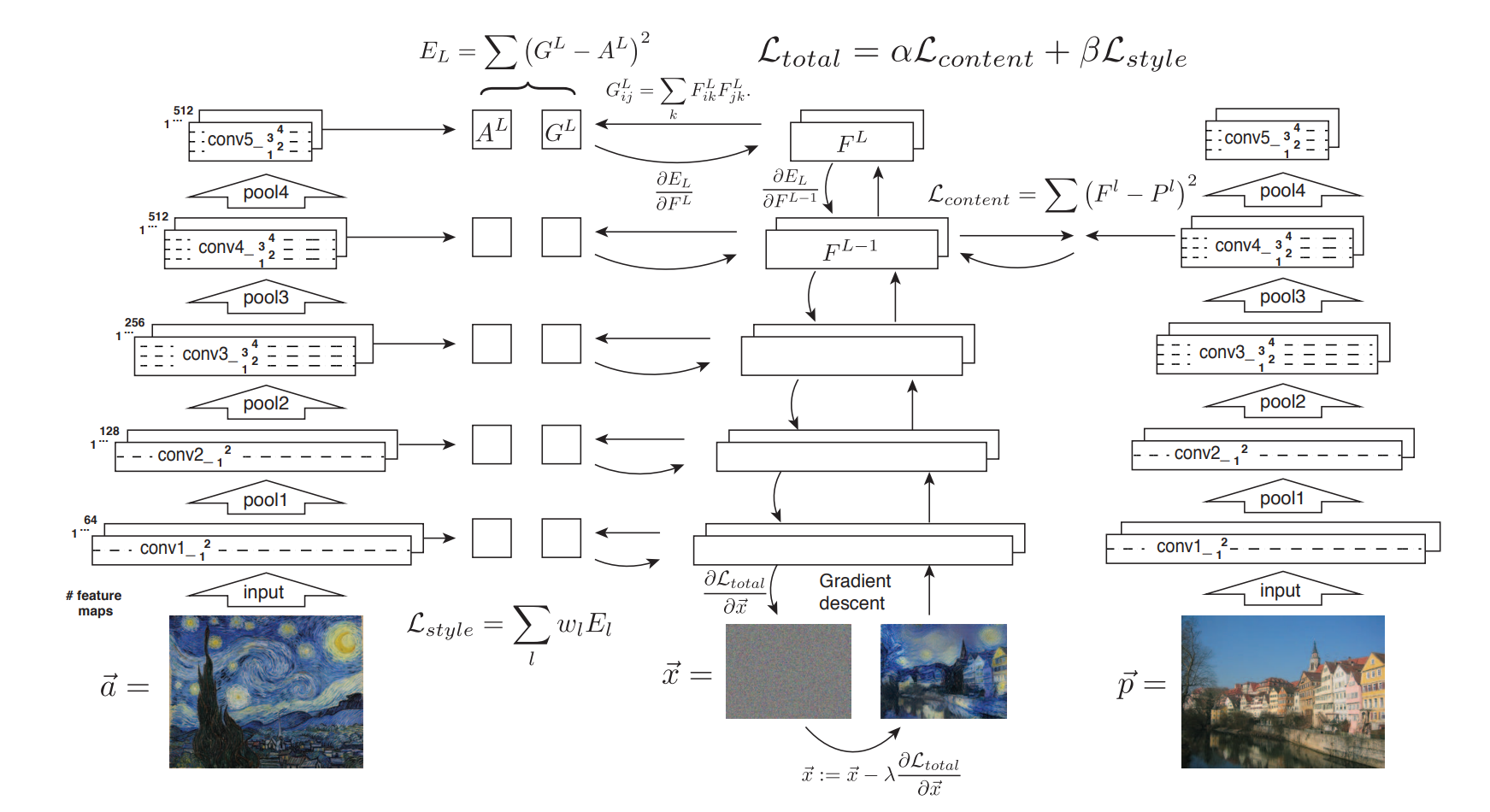
记 $\vec{a}$ 为原始图像，$\vec{x}$ 为待生成的图像，$A^l$ 和 $G^l$ 是 layer $l$ 上对应的风格表示。layer $l$ 对总损失的贡献为：

$E_l = \frac{1}{4N^2_l M^2_l} \sum_{i,j} (G^l_{ij}-A^l_{ij})^2$

那么总的损失就是：

$\cal{L}_{style}(\vec{a}, \vec{x}) = \sum_{l=0}^{\it{L}} w_l \it{E}_l$

其中，$w_l$ 是不同 layer 的权重系数。

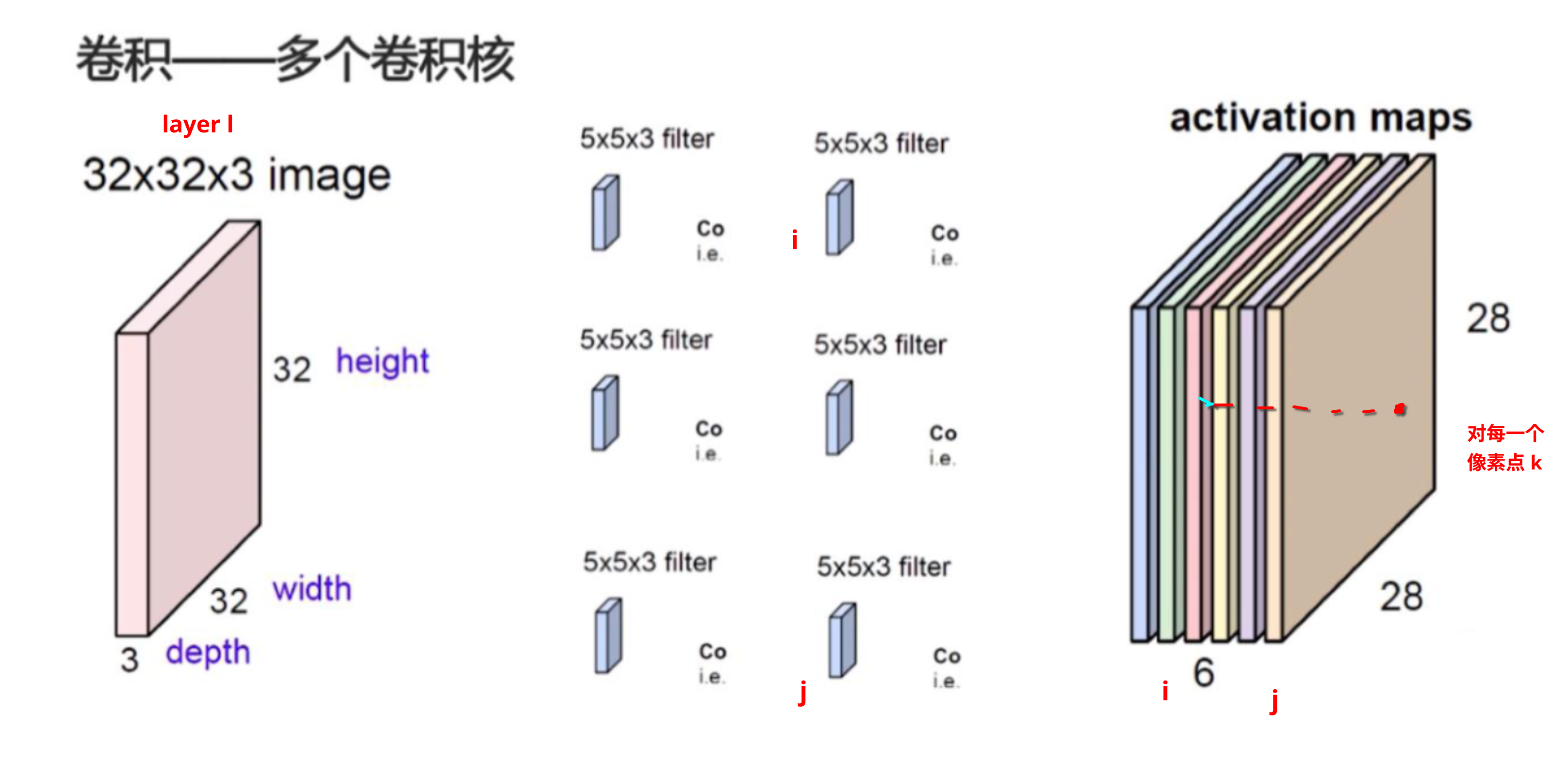
那么，可对 $E_l$ 求导（激活函数 relu 之后）。我们要求的是：

$\frac{\partial E_l}{\partial F^l_{pq}}$

这个相当于对 activation map 中的某一个像素值求导。其中，$p$ 表示第 $p$ 个特征图（滤波器），$q$ 表示该特征图中的第 $q$ 个空间位置。

$E_l = \frac{1}{4N^2_l M^2_l} \sum_{i,j} \left( \sum_k F^l_{ik}F^l_{jk} - A^l_{ij} \right) ^2$

对 $F^l_{pq}$ 求导数时，只考虑那些包含 $F^l_{pq}$ 的项。观察 Gram 矩阵的定义，我们发现 $F^l_{pq}$ 会出现在所有满足 $i = p$ 或 $j = p$ 的项中。

所以对单个项 $(G^l_{ij} - A^l_{ij})^2$ 的导数如下：

情况 1，当 $i = p$ 时：

$\frac{\partial G^l_{ij}}{\partial F^l_{pq}} = \frac{\partial}{\partial F^l_{pq}} \sum_k F^l_{ik} F^l_{jk} = F^l_{jq} \quad (\text{因为 } i=p, \text{而 } k=q)$

情况 2，当 $j = p$ 时：

同理：

$\frac{\partial G^l_{ij}}{\partial F^l_{pq}} = F^l_{iq}$

（如果 $i = j = p$，那就变成两项相加）

于是：

$\begin{aligned} \frac{\partial E_l}{\partial F^l_{pq}} &= \frac{1}{4 N_l^2 M_l^2} \sum_j 2 (G^l_{pj} - A^l_{pj}) F^l_{jq} + \sum_i 2 (G^l_{ip} - A^l_{ip}) F^l_{iq} \\ &= \frac{1}{2 N_l^2 M_l^2} \left[ \sum_j (G^l_{pj} - A^l_{pj}) F^l_{jq} + \sum_i (G^l_{ip} - A^l_{ip}) F^l_{iq} \right] \\ \end{aligned}$

这个结果不够美观，可以使用矩阵乘法的一些小技巧化简一下。

注意到

$\sum_j (G^l_{pj} - A^l_{pj}) F^l_{jq}$

是对第 $p$ 行的 Gram 差值与第 $q$ 列的特征图相乘：

类似地，对于

$\sum_i (G^l_{ip} - A^l_{ip}) F^l_{iq}$

是对第 $p$ 列的 Gram 差值与第 $q$ 列的特征图相乘：

对于上面的两个式子，只需要按照 dot product 的方法算出两个数值即可。 （自行体会）

既然只需要算出数值，为了简化形式，我们可以尝试合并。同时，我们注意到一个很好的性质：

$(G^l - A^l) = (G^l - A^l)^T$

且 $(G^l - A^l)$ 是对称阵，形状为 $N_l \times N_l$ .

我们很有注意力地简化为：

$\frac{\partial E_l}{\partial F^l_{pq}} = \frac{1}{N^2_l M^2_l} \left( (F^l)^T (G^l - A^l)^T \right)_{qp}$

注意细节：$p$ 和 $q$ 交换了位置。这是为了统一形式，做了转置之后位置也要对应上。

可以进一步简化为：

$\frac{\partial E_l}{\partial F^l_{pq}} = \frac{1}{N^2_l M^2_l} \left( (F^l)^T (G^l - A^l) \right)_{qp}$

实际上还要经过一次 relu, 因为在大于 0 的时候 relu 相当于恒等映射，小于 0 时值变为 0，所以最终的公式是：

$\frac{\partial E_l}{\partial F^l_{pq}} = \begin{cases} \frac{1}{N_l^2 M_l^2} \left( (F^l)^T (G^l - A^l) \right)_{qp} & F^l_{pq} > 0 \\ 0 & F^l_{pq} < 0 \end{cases}$

为了综合考虑内容损失和风格损失：

$\cal{L}_{total} (\vec{p}, \vec{a}, \vec{x}) = \alpha \cal{L}_{content} (\vec{p}, \vec{x}) + \beta \cal{L}_{style} (\vec{a}, \vec{x})$

关于代码实现，请参考此链接。

拓展

另一个版本：

可以用 Google Lens 搜图，查论文。

Embedding

为什么要提出 embedding? Embedding 可以干什么？

https://blog.csdn.net/qq_35799003/article/details/84780289
以上链接内容已备份（github 对应链接）

理解 Embedding 原理：

秒懂词向量Word2vec的本质，备份

本 notebook 包含的内容：

数据集imdb，电影分类，分电影是积极的，还是消极的
变长输入
keras.preprocessing.sequence.pad_sequences()
embedding 理解
keras.layers.Embedding()
keras.layers.GlobalAveragePooling1D()

RNN

RNN 的基础知识： https://zhuanlan.zhihu.com/p/30844905 （已在 github 对应仓库备份）

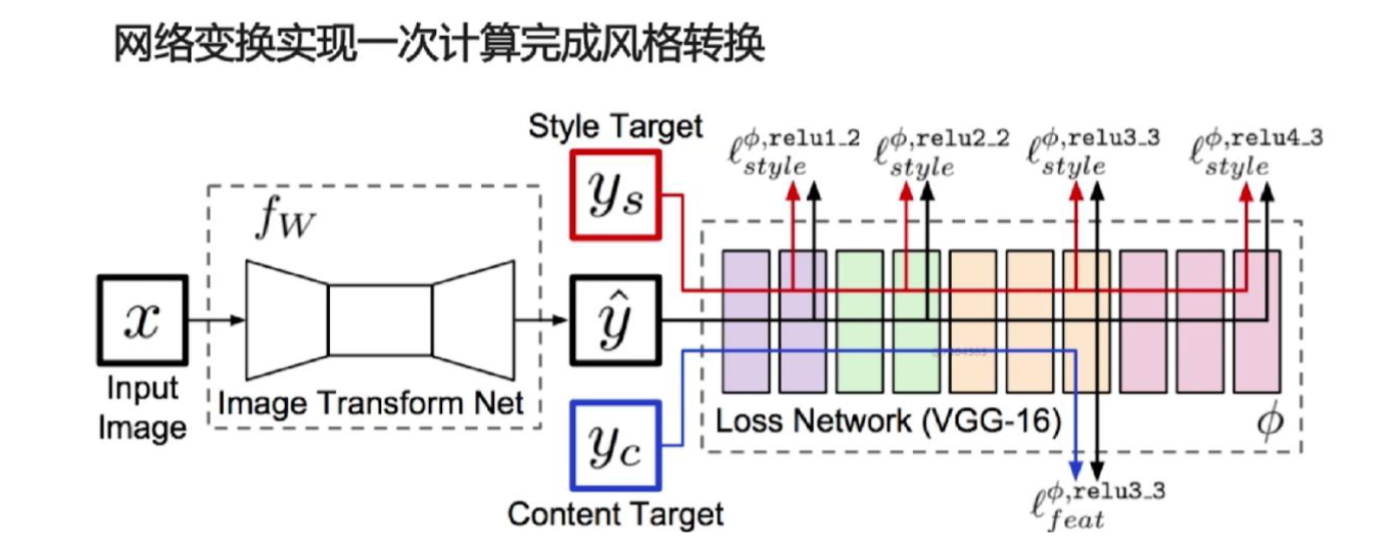
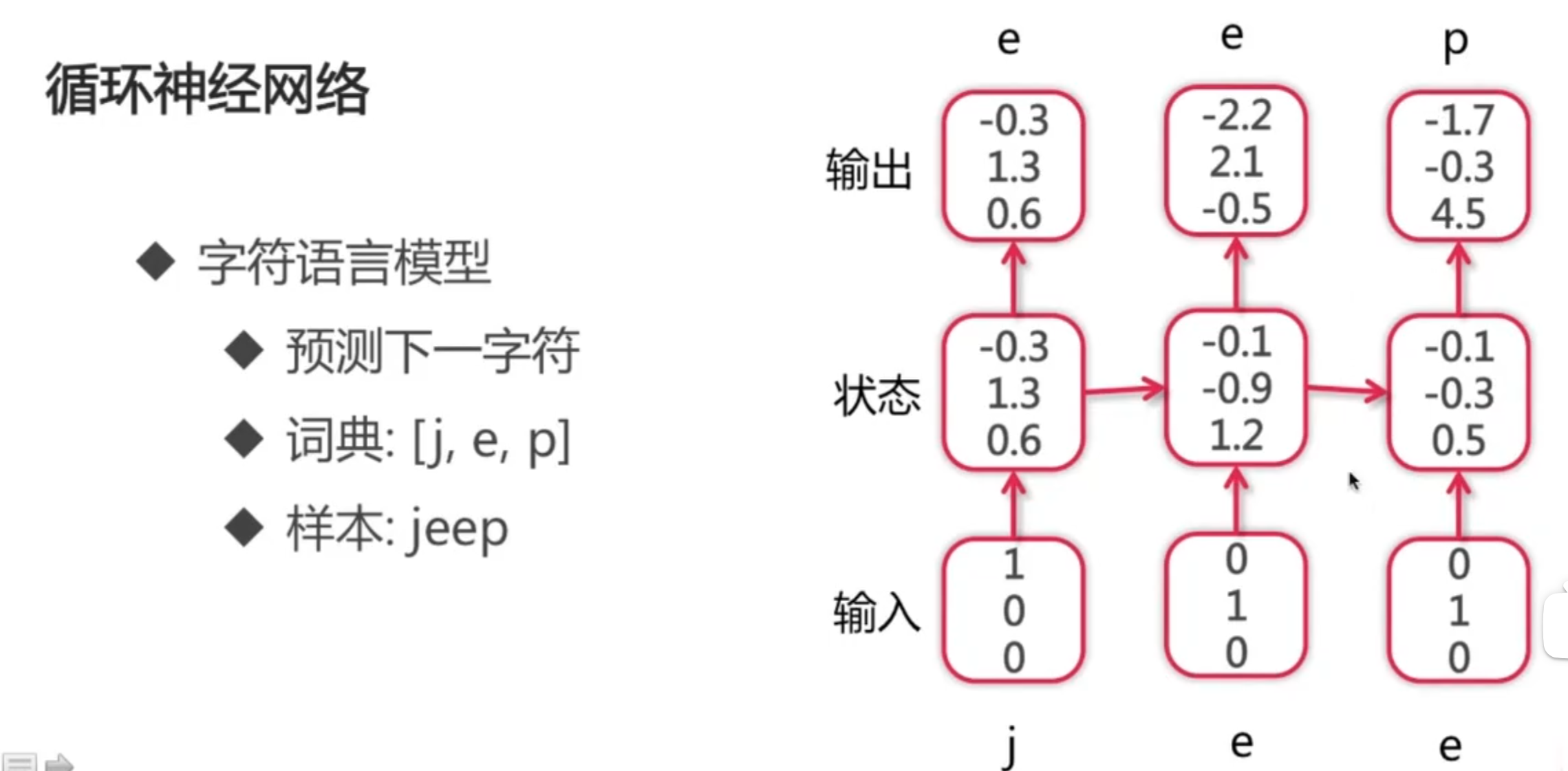
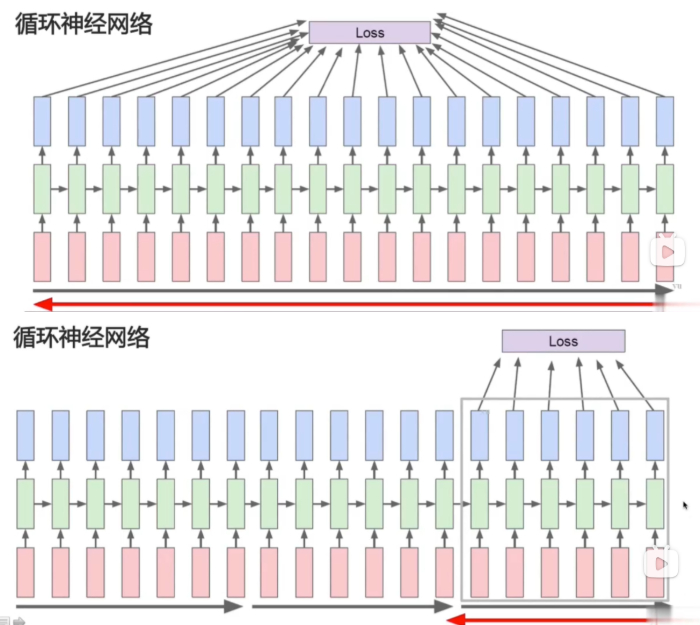
RNN 的一个经典应用（例如可以用于输入法的下一个词预测）：

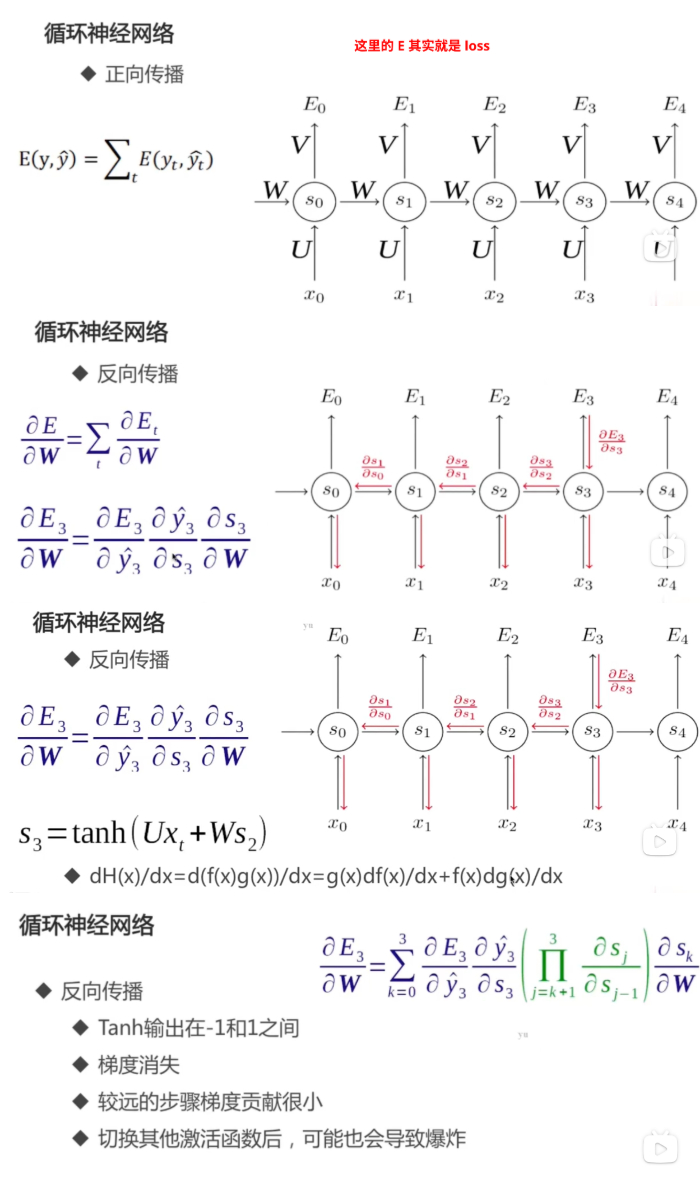
RNN 的反向传播：

较远的步骤梯度贡献很小，实践中可以把他们忽略：

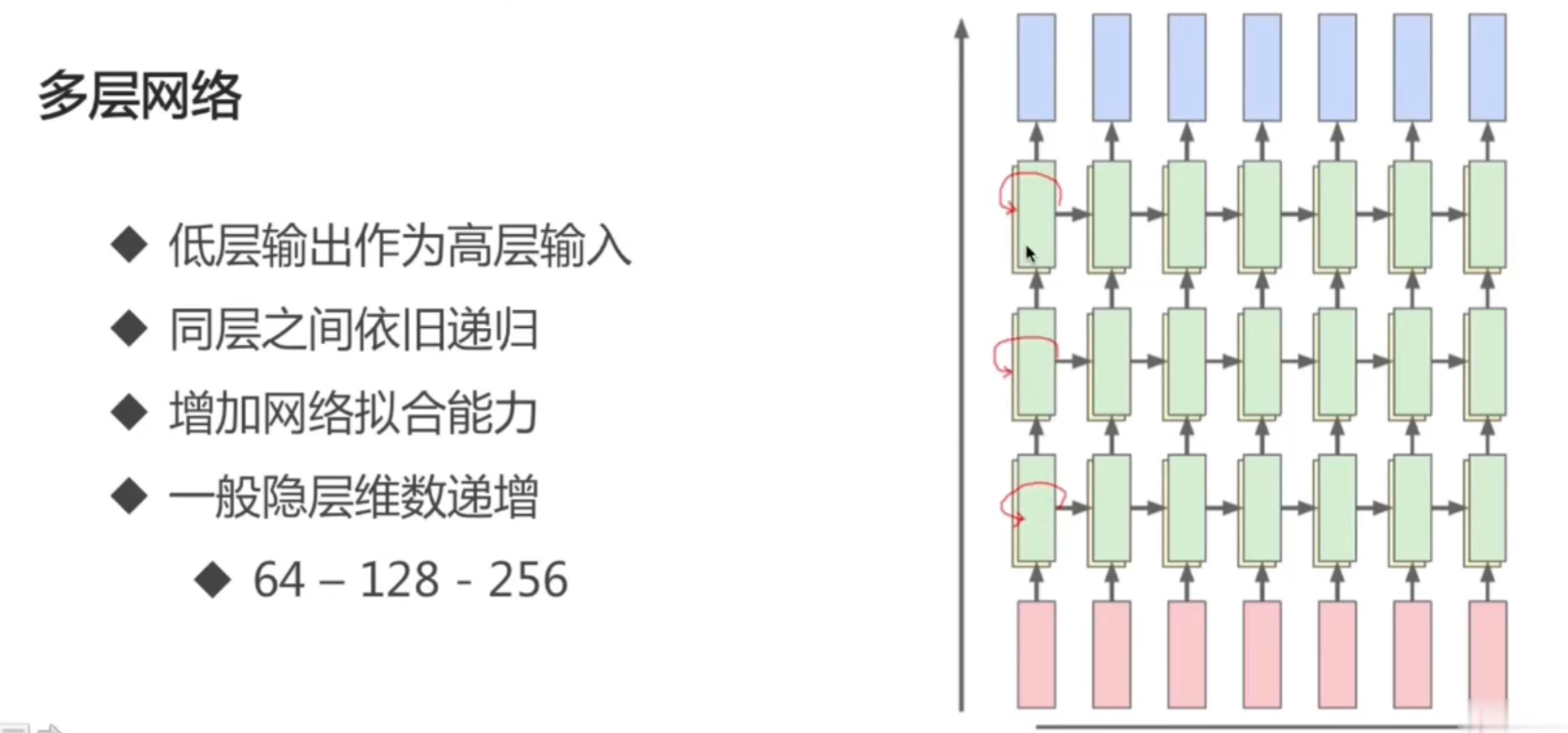
自然，可以有多层的 RNN：

类似地，也可以在 RNN 上搞残差连接，按下不表。

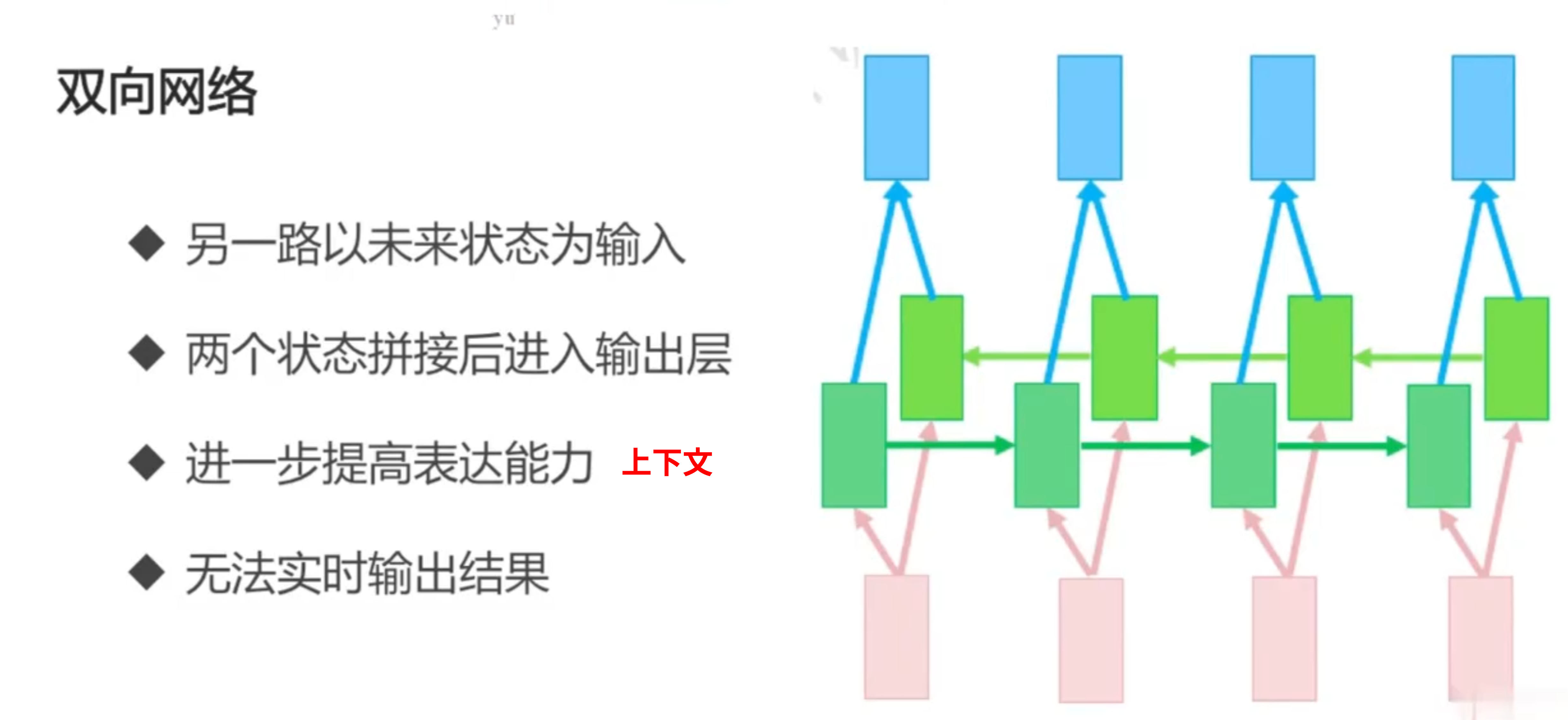
双向网络（上下文）：

本 notebook 包含的内容：

imdb 数据集（完成任务同上一个）
keras.layers.SimpleRNN()
keras.layers.Bidirectional()

BRNN（双向RNN）的应用包括（ref: Wikipedia）：

语音识别（与长时记忆结合）
翻译
手写识别
蛋白质结构预测
词性标记
依赖解析
实体提取

文本生成实战
本 notebook 包含的内容：

莎士比亚数据集
生成文本的原理
模型的保存与加载
该模型的评价
Squeeze, expand_dims

长短期记忆网络 LSTM

为什么需要 LSTM？
普通 RNN 的信息不能长久传播：离结尾较远的信息被稀释的比较厉害。

LSTM 引入选择性机制：

选择性输出
选择性输入
选择性遗忘

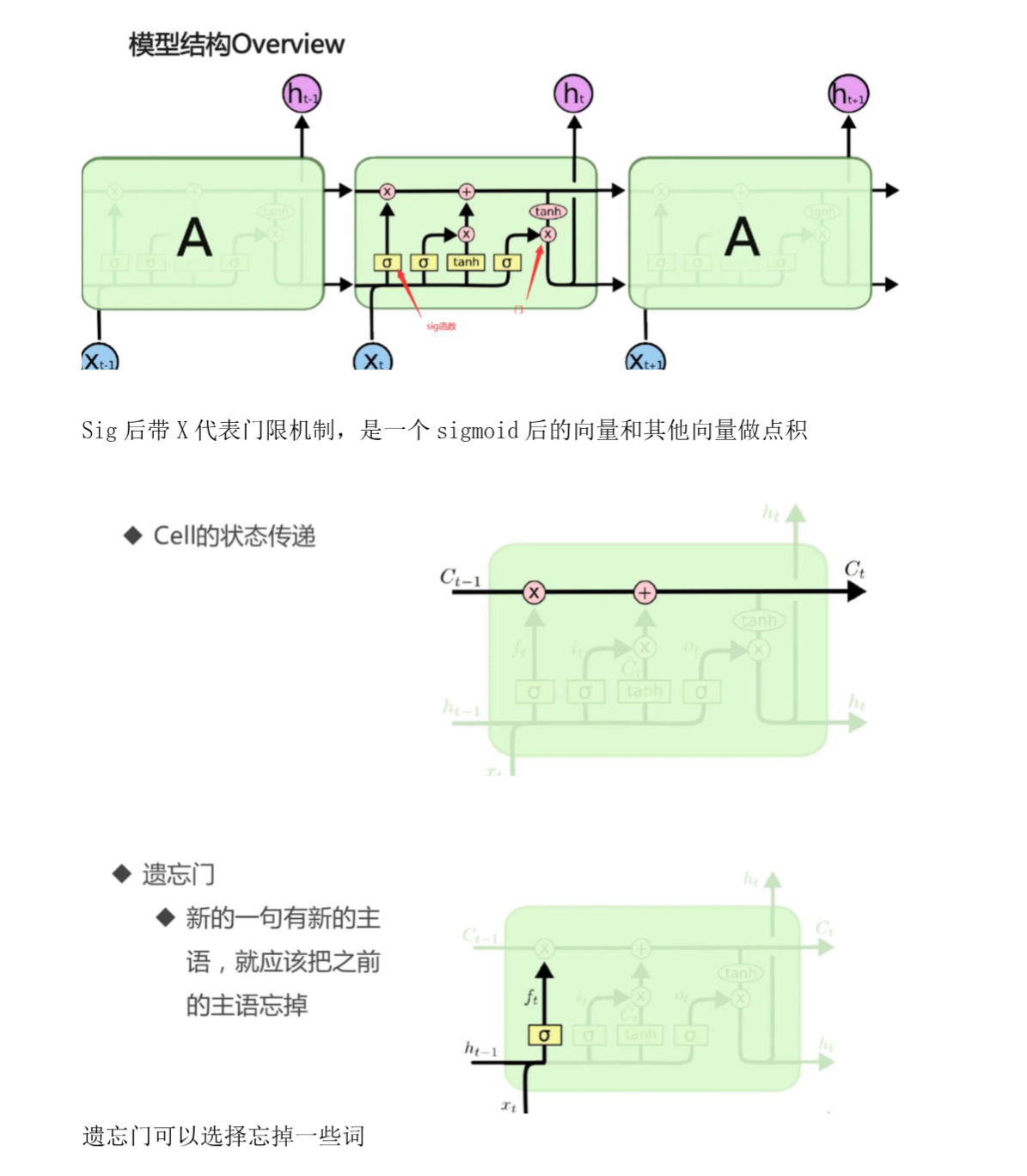
选择性机制实现的原理：门。

向量 A -> sigmoid -> [0.1, 0.9, 0.4, 0, 0.6]
向量 B -> [13.8, 14, -7, -4, 30.0]
A 为门限，B 为信息，两个相乘（点积）
A dot B = [1.38, 12.6, -2.8, 0, 18.0]

ref: https://blog.csdn.net/weixin_44162104/article/details/88660003

总览：

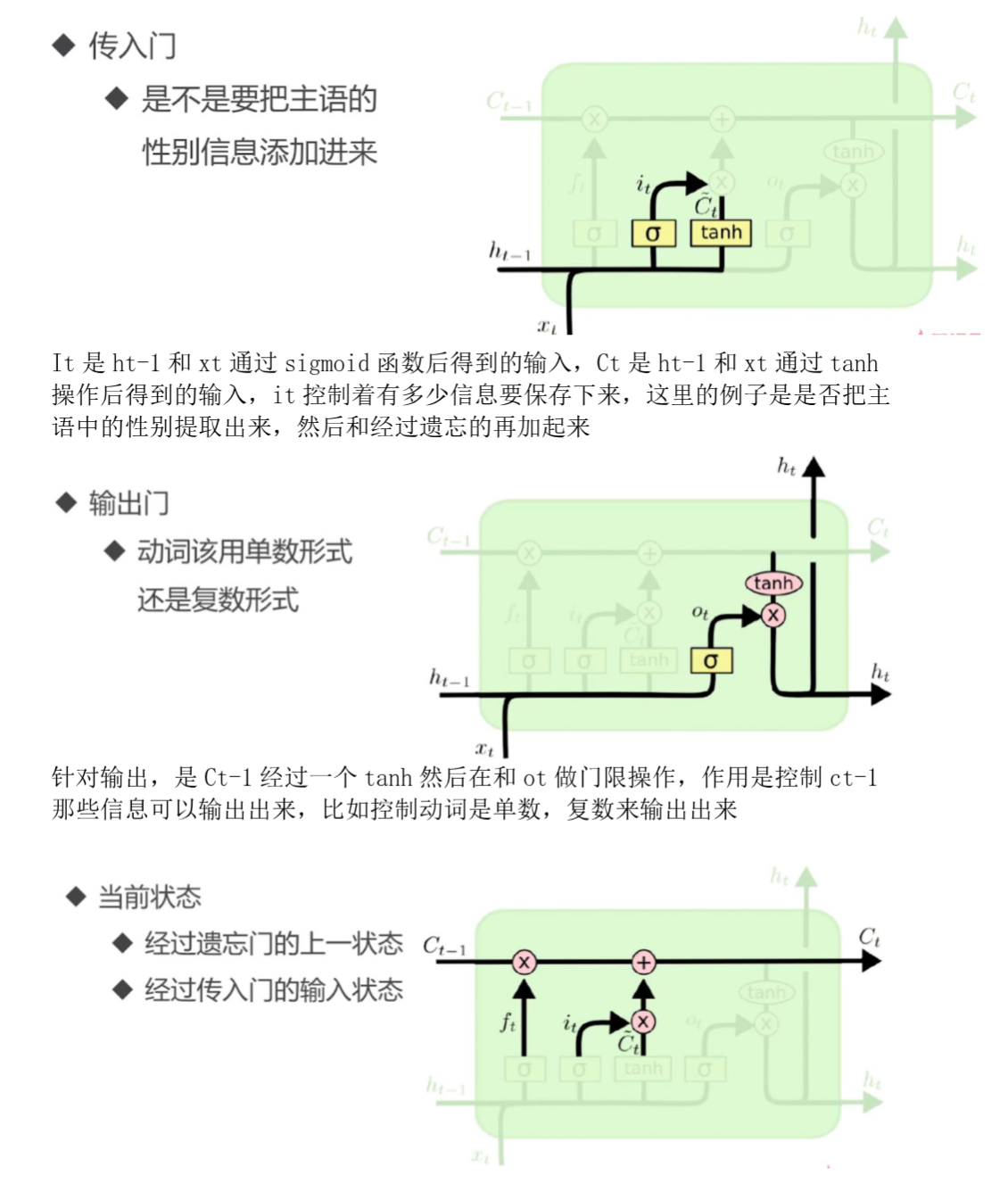
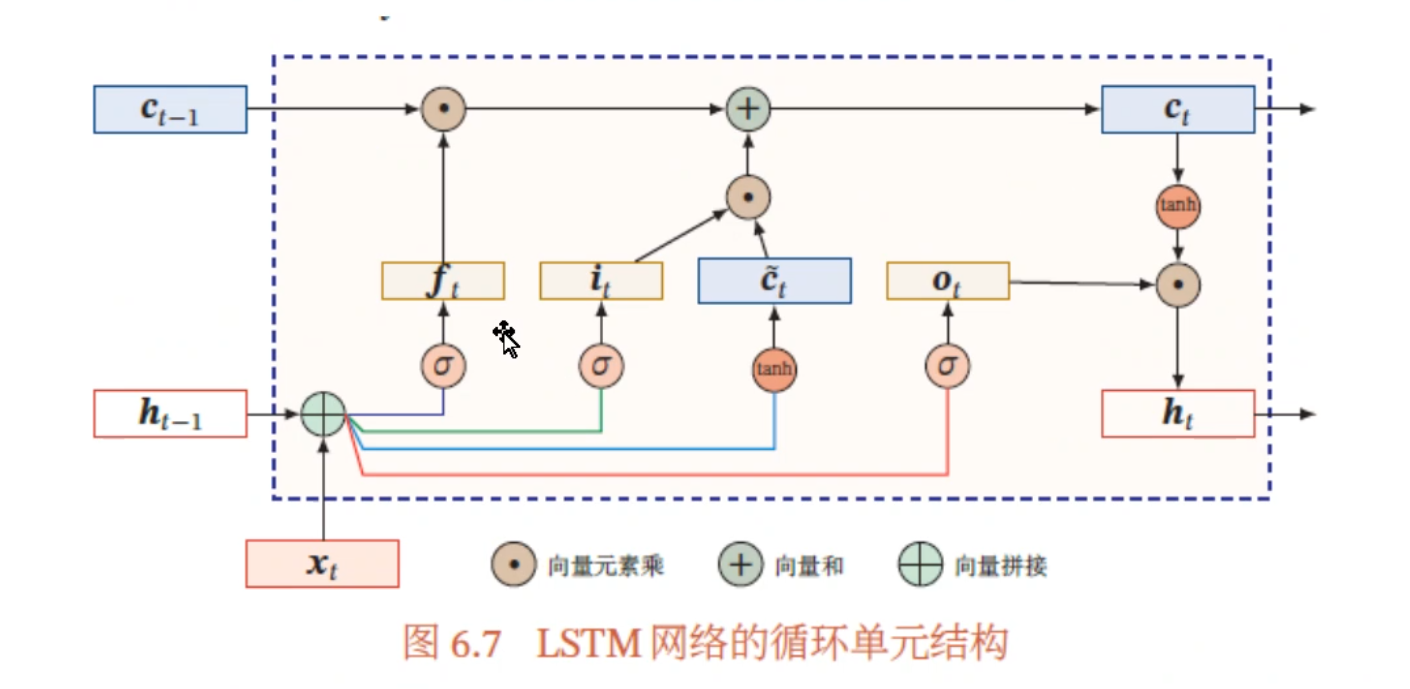
从微观上看，LSTM 引入了细胞状态，并使用输入门、遗忘门、输出门来保持和控制信息。具体地，LSTM 某个 timestep $t$ 的计算公式如下：

$\begin{aligned} f_t & = \sigma (W_f \cdot [h_{t-1}, x_t] + b_f) \\ i_t & = \sigma (W_i \cdot [h_{t-1}, x_t] + b_i) \\ \tilde{c}_t & = \tanh (W_c \cdot [h_{t-1}, x_t] + b_c) \\ c_t & = f_t * c_{t-1} + i_t * \tilde{c}_t \\ o_t & = \sigma (W_o \cdot [h_{t-1}, x_t] + b_o) \\ \end{aligned}$

其中，$f_t$ 为遗忘门，$i_t$ 为输入门，$o_t$ 为输出门，$c_t$ 为细胞状态，$\tilde{c}_t$ 为细胞状态候选值，$h_t$ 为隐藏层状态值，$W$ 和 $b$ 为权重和偏置。

LSTM 既能够处理短期依赖问题，又能够处理长期依赖问题。

实战： RNN/tf47-embedding-lstm.ipynb

imdb 数据集
LSTM 文本分类

实战： RNN/tf48-embedding-lstm-subword.ipynb

subword
- Subword-level 是介于 char-level 和 word-level 之间的设计，很多机器翻译都会用 subword
- 词典比 word level 小，embedding 参数变少，训练时间缩短
imdb 数据集

GPU Strategy

引入

如何默认用全部 GPU 并且内存全部占满？

如何不浪费内存和计算资源?

内存自增长
虚拟设备机制

多 GPU 使用

虚拟 GPU ；实际 GPU
手工设置；分布式机制

API 列表（旧的 tensorflow API，可能已经过时）：

tf.debugging.set log_device_placement 某个变量分配在哪个设备上
tf.config.experimental.set_visible_devices 本进程可见的设备
tf.config.experimental.ist logical_devices 获取逻辑设备
tf.config.experimentalist physical_devices 获取物理设备
tf.config.experimental.set_memory_growth 用多少，设置多少
tf.config.experimental.VirtualDeviceConfiguration 建立逻辑分区
tf.config.set_soft_device_placement 自动把某个计算分配到某个设备上，不容易出错

使用多 GPU 的实际例子：

使用 tf.distribute.Strategy 进行自定义训练，分布式训练官方实例
TensorFlow 分布式训练，多机
分布式TensorFlow多主机多GPU原理与实现，已在 github 相应仓库备份
Cifar10 的多 GPU 代码参考

分布式策略

为什么需要分布式？数据量太大，模型太复杂。

本小节以 tensorflow 为例。

MirroredStrategy

同步式分布式训练，适用于一机多卡情况。

每个 GPU 都有网络结构的所有参数，这些参数会被同步。

数据并行

Batch 数据切为 N 份分给各个 GPU
梯度聚合然后更新给各个 GPU 上的参数

CentralStorageStrategy

MirroredStrategy 的变种。参数不是在每个 GPU 上，而是存储在一个设备上。

除了更新参数的计算之外，计算是在所有 GPU 上并行的。

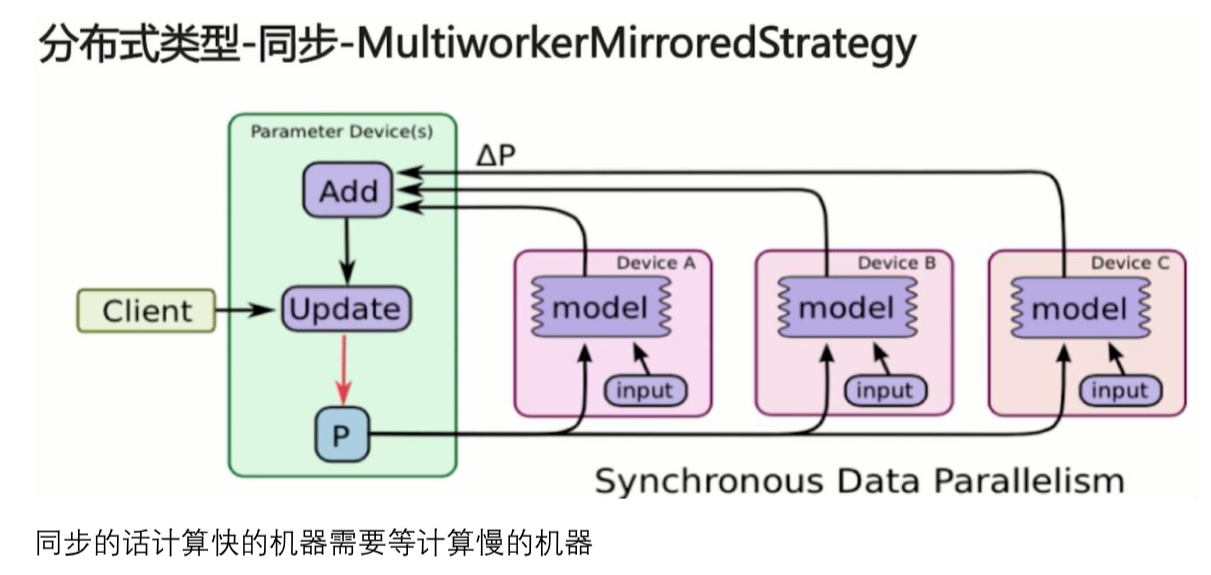
MultiWorkerMirroredStrategy

类似于 MirroredStrategy，适用于多机多卡情况。

TPUStrategy

与 MirroredStrategy 类似，使用在 TPU 上的策略。

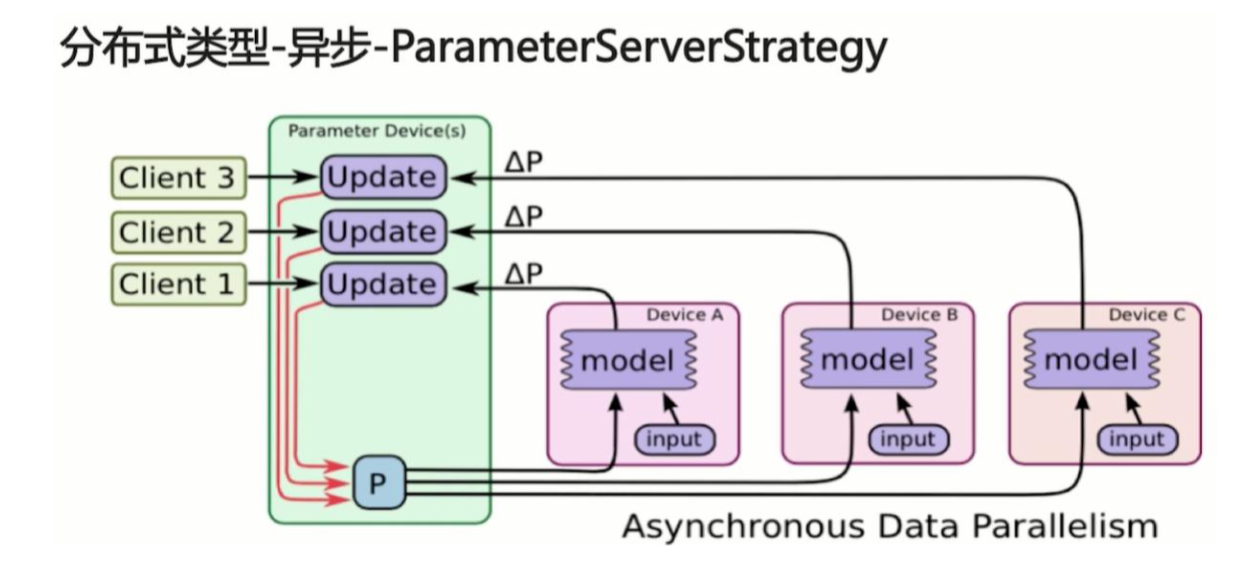
ParameterServerStrategy

异步分布式，更加适用于大规模分布式系统。

机器分为 Parameter Server 和 worker 两类：

Parameter server 负责整合梯度，更新参数
Worker 负责计算，训练网络

Tensorflow 一开始支持分布式的时候，便是这种 parameter server 架构。TensorFlow 一般将任务分为两类 job：一类叫参数服务器，parameter server，简称为 ps，用于存储可训练的参数变量 tf.Variable；一类就是普通任务，称为 worker，用于执行具体的计算。

同步与异步的优劣

异步可以避免短板效应

多机多卡（不同机器的显卡类型往往不一致）

异步的计算会增加模型的泛化能力

异步不是严格正确的，所以模型更容忍错误

同步可以避免过多的通信

一机多卡

初识 TensorFlow

Tensorflow-keras

简介

tf_keras做分类

tf_keras做回归

梯度消失、梯度爆炸

问题描述

批归一化

更改激活函数

Dropout

Wide & Deep 模型（推荐场景）

超参数搜索

Batch Size

学习率衰减

离散下降（discrete staircase）

指数减缓（exponential decay）

网格搜索、随机搜索

tensorflow 基础 API

dataset

estimator

卷积神经网络

全连接层的困境

卷积的思路

局部连接

卷积操作、参数共享

池化

实战

迁移学习

ResNet

基本知识

实战

卷积神经网络进阶

AlexNet

VGGNet

ResNet

InceptionNet

MobileNet

不同模型结构的对比

卷积神经网络调参

不同的优化器

前情提要 - 梯度下降

AdaGrad

RMSProp

Adam

激活函数

Sigmoid

Tanh

ReLU

Leaky-ReLU

ELU

Maxout

总结

网络初始化（w和b）

批归一化

数据增强

更多调参技巧

实战

图像风格变换

神经网络可以做什么

卷积神经网络学到了什么

图像风格转换（简单版本）

拓展

Embedding

RNN

长短期记忆网络 LSTM

GPU Strategy

引入

分布式策略

MirroredStrategy

CentralStorageStrategy

MultiWorkerMirroredStrategy

TPUStrategy

ParameterServerStrategy

同步与异步的优劣