Fourier Stuff

前置知识

方程 $z^n=1\quad (n=1,2,3,\cdots)$ 的复数根 $z$ 为 $n$ 次单位根^[1]。

下面求解该方程。

已知欧拉公式^[2]：

$e^{i\pi}+1=0$

则：

$(e^{i\pi})^2=(-1)^2$ $e^{2i\pi}=1$

两边作 $k$ 次方：

$e^{i2k\pi}=1$

再取 $n$ 次根，得：

$\sqrt[n]{1}=e^{i2\pi \frac{k}{n}}=\cos 2\pi \frac{k}{n}+i\sin 2\pi \frac{k}{n}$

由三角函数的周期性易知，其根有 $n$ 个，分别是 $k$ 取 $0,1,2,\cdots ,n-1$

即，单位的 $n$ 次根有 $n$ 个：

$e^{\frac{2\pi ki}{n}} \quad (k=0,1,2,\cdots ,n-1)$

单位的 $n$ 次根以乘法构成 $n$ 阶循环群，生成元是 $n$ 次本原单位根。$n$ 次本原单位根是 $e^{\frac{2\pi ki}{n}}$ ，其中 $k$ 和 $n$ 互质。因此由欧拉函数定义，$n$ 次本原单位根数目为欧拉函数 $\varphi (n)$ .

例子：

一次单位根有一个：$1$
二次单位根有两个：$+1$ 和 $-1$ ，只有 $-1$ 是本原根
三次单位根是（除 1 外都是本原根）： $\{1,\frac{-1+\sqrt{3}i}{2},\frac{-1-\sqrt{3}i}{2}\}$
四次单位根是：$\{1,+i,-1,-i\}$ ，其中 $+i$ 和 $-i$ 是本原根

当 $n$ 不小于 2 时，n 次单位根总和为 0 .

$\sum\limits_{k=0}^{n-1}e^{\frac{2\pi ki}{n}}=\frac{e^{\frac{2\pi kni}{n}}-1}{e^{\frac{2\pi i}{n}}-1}=\frac{1-1}{e^{\frac{2\pi i}{n}}-1}=0$

该结果在复平面上是显然的。

FFT 多项式乘法

部分内容参考自视频 The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever? 只有生肉，没有找到较好的翻译版本。因此使用了部分英语表述。这个视频在记法上有一些蛊惑人心的地方，我就按照自己的习惯来了。

问题引入：我们试图计算两个多项式的乘积。朴素的做法是使用乘法的分配律在 $O(n^2)$ 时间内完成。现在需要寻找更高效的算法。

为此引入 Polynomial Representation 的另一种方法：value representation.

Coefficient Representation :

$P(x)=p_0+p_1x+p_2x^2+\cdots p_dx^d$ $\begin{matrix} \underbrace{[p_0,p_1,\cdots ,p_d]} \\ {\scriptstyle\text{Coefficient Representation}} \end{matrix}$

Value Representation :

$\begin{matrix} \underbrace{\{(x_0,P(x_0)),(x_1,P(x_1)),\cdots ,(x_d,P(x_d))\}} \\ {\scriptstyle\text{Value Representation}} \end{matrix}$

两者之间的关系：

$(d+1)$ points uniquely define a degree $d$ polynomial.

$e.g.$

$\{(-1,0),(0,1),(1,0),(2,1)\}$

Corresponds to

$P(x)=\frac{2}{3}x^3-x^2-\frac{2}{3}x+1$

$Proof.$

$\begin{bmatrix} P(x_0) \\ P(x_1) \\ \vdots \\ P(x_d) \end{bmatrix}=\begin{bmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^d \\ 1 & x_1 & x_1^2 & \cdots & x_1^d \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_d &x_d^2 & \cdots & x_d^d \end{bmatrix}\begin{bmatrix} p_0 \\ p_1 \\ \vdots \\ p_d \end{bmatrix}$

Clearly, the determinant of the matrix above is the Vandermonde determinant.

Since the chosen values of $x_i (i=0,1,2,\cdots ,d)$ are distinct from each other, the Vandermonde determinant is non-zero.

$\det \begin{pmatrix}\begin{bmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^d \\ 1 & x_1 & x_1^2 & \cdots & x_1^d \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_d &x_d^2 & \cdots & x_d^d \end{bmatrix}\end{pmatrix}=\prod_{0\leqslant j<i\leqslant d}(x_i-x_j)\neq 0$

Therefore, the matrix is invertible, and the equation has a unique solution.

Hence, a bijection is established between the value representation and the coefficient representation of the polynomial through this matrix. $(d+1)$ points uniquely define a degree $d$ polynomial.

■

有了两个多项式的 value representation ，就可以很容易地计算出这两个多项式的乘积的 value representation.

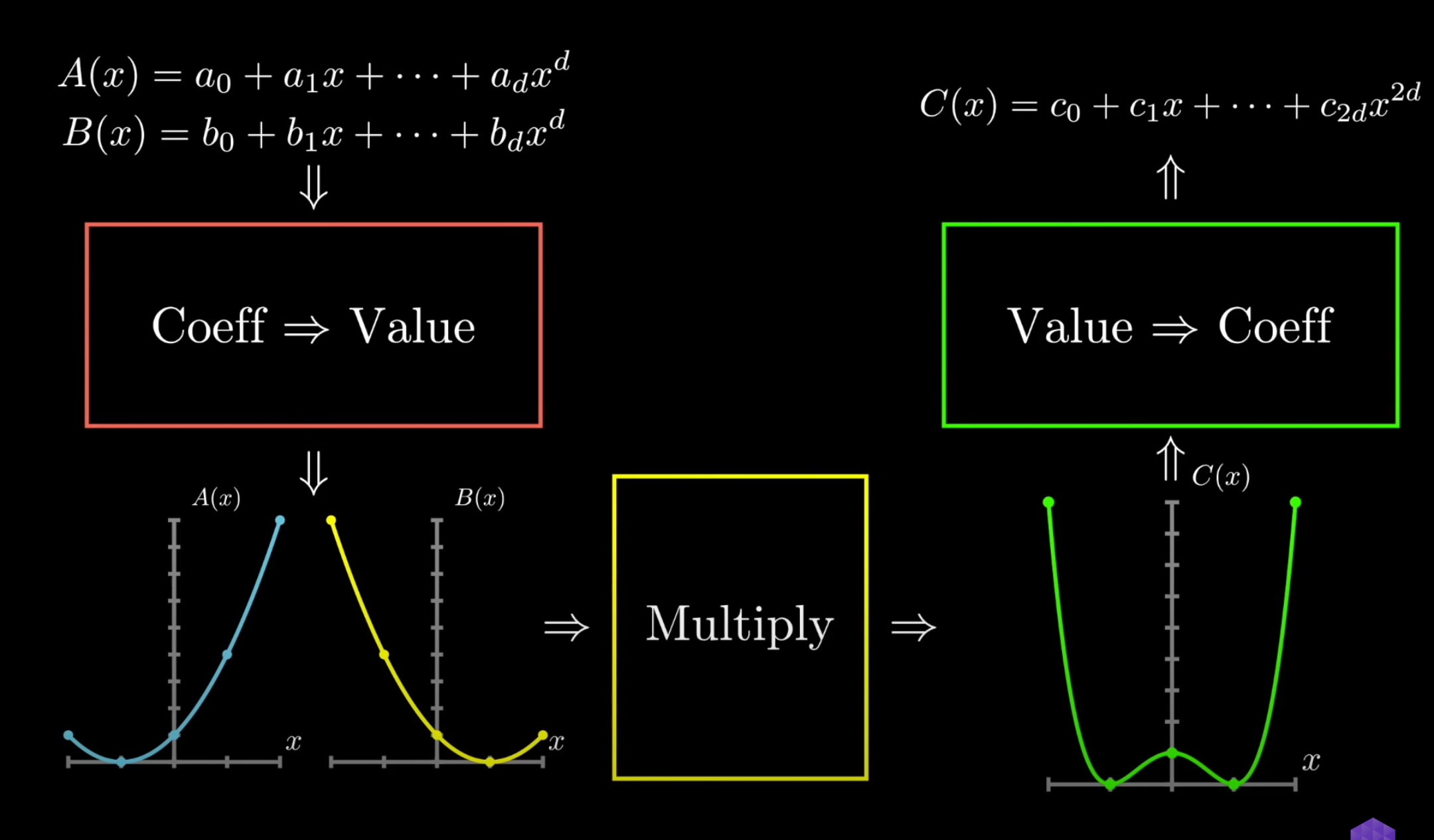
整个过程的大致思路如下：

首先考虑 Coeff 到 Value 的转换。

我们尝试计算 n-1 次多项式 $P(x)$ 在

$x=\pm x_1,\pm x_2,\cdots ,\pm x_{n/2}$

处的值，寻找能减少计算量的思路。

将 $P(x)$ 按项的次数奇偶分类：

$P(x)=P_e(x^2)+xP_o(x^2)$

得到 $P_e(x)$ 和 $P_o(x)$ . 于是：

$P(\pm a)=P_e(a^2)\pm aP_o(a^2)$

于是问题转化为求 $P_e(x)$ 和 $P_o(x)$ 在 $a^2$ 处的值，这个过程似乎可以递归地进行。而且这两个多项式的次数比原来下降了一半。看起来很 nice .

而问题是，进入第二层递归时，我们的采样点就不是相反数对了。递归失败。

以上尝试给出了有益的思路，接下来为了制造相反数对，考虑将数域拓展到复数。

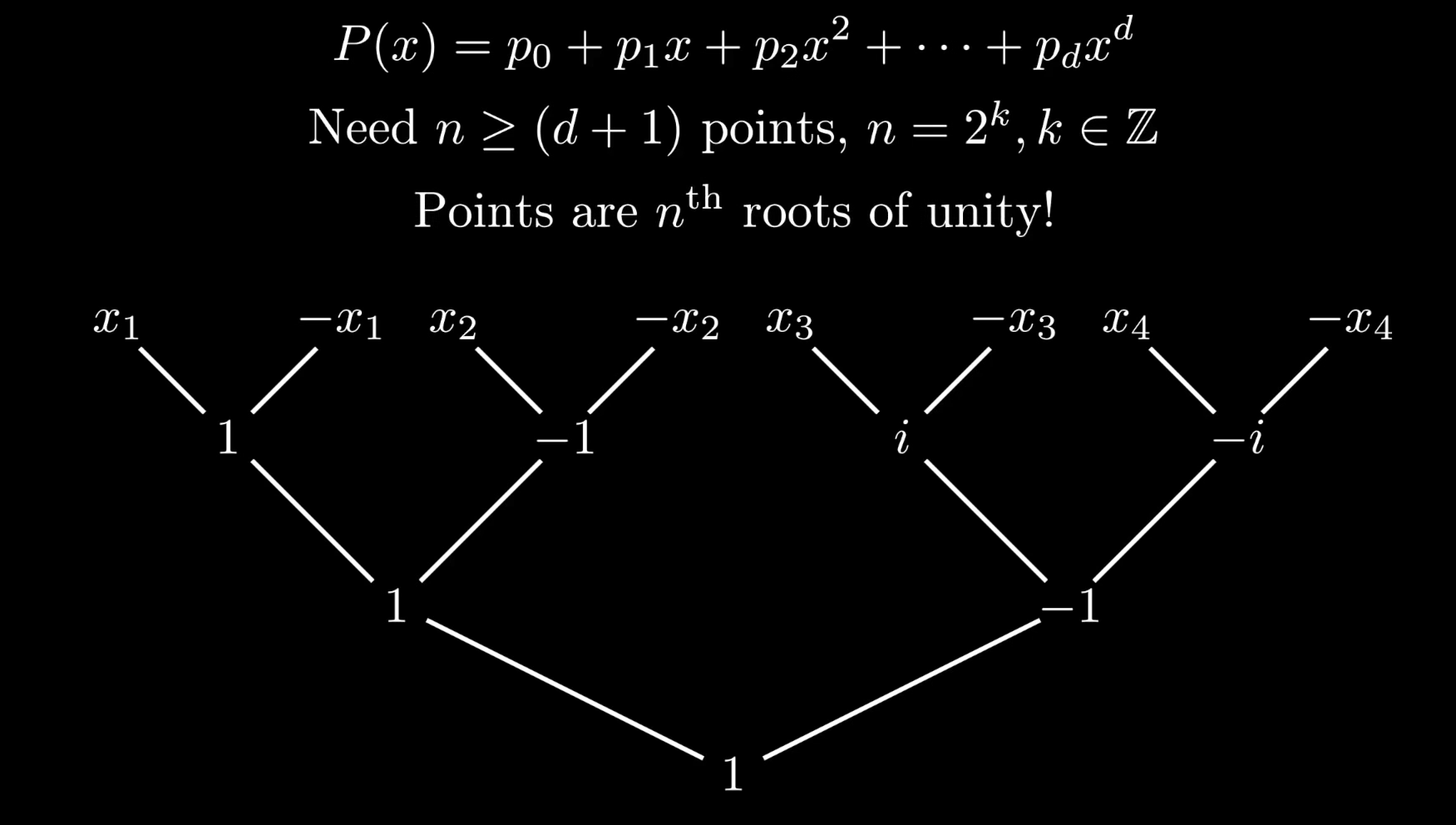
在下图中，任一节点的值的平方等于父节点的值：

满足我们想要的性质。注意这里为方便原理展示对采样点数目 $n$ 作了限制：$n=2^k,k\in \mathbb{N}$ . 同时这也是对多项式次数的限制。

依据在前置知识中的结论，单位根在复平面中如下所示：

并且，由相关性质，可以得到相反数对：

$\omega ^{j+n/2}=-\omega ^j$

下面总结一下算法的流程。

为求出 n-1 次多项式 $P(x)$ 的 value representation ，需要计算其在

$x=\omega ^0,\omega ^1,\cdots ,\omega ^{n-1} \quad | \quad \omega =e^{\frac{2\pi i}{n}}$

处的值。为了减少计算量，将 $P(x)$ 按项的次数奇偶分类：

$P(x)=P_e(x^2)+xP_o(x^2)$

由是发现需要求解 $P_e(x)$ 和 $P_o(x)$ 在

$\omega ^0,\omega ^2,\omega ^4, \cdots ,\omega ^{n-2}$

处的值。这个过程可以递归地完成。

注意这里就是原视频蛊惑人心的地方，UP主在记法上的不严谨可能会导致理解上的困难。$P_e(x)$ 和 $P_o(x)$ 是将公式 $P(x)=P_e(x^2)+xP_o(x^2)$ 右侧的多项式 $P_e(x^2)$ 和 $P_o(x^2)$ 看作 $x^2$ 的函数用 $x$ 改写得到的。

假设递归成功，就得到了 $P_e(x)$ 和 $P_o(x)$ 的 value representation . 记数组（从 0 开始编号）：

$y_e[...]=[P_e(\omega ^0),P_e(\omega ^2),\cdots ,P_e(\omega ^{n-2})]$ $y_o[...]=[P_o(\omega ^0),P_o(\omega ^2),\cdots ,P_o(\omega ^{n-2})]$

现在要做的是，由此得到原来的多项式的 value representation .

在上面得到的公式

$P(\pm a)=P_e(a^2)\pm aP_o(a^2)$

中，令 $a=\omega ^j$ 得：

$P(\pm \omega ^j)=P_e(\omega ^{2j})\pm \omega ^jP_o(\omega ^{2j})$

再由 $\omega ^{j+n/2}=-\omega ^j$ 得：

$P(\omega ^j)=P_e(\omega ^{2j})+ \omega ^jP_o(\omega ^{2j})$ $P(\omega ^{j+n/2})=P_e(\omega ^{2j})- \omega ^jP_o(\omega ^{2j})$ $j\in \{0,1,\cdots ,\frac{n}{2}-1 \}$

又因为

$y_e[j]=P_e(\omega ^{2j})$ $y_o[j]=P_o(\omega ^{2j})$

于是

$P(\omega ^j)=y_e[j]+ \omega ^jy_o[j]$ $P(\omega ^{j+n/2})=y_e[j]- \omega ^jy_o[j]$ $j\in \{0,1,\cdots ,\frac{n}{2}-1 \}$

最后返回该层多项式的 value representation 即可。

伪代码如下：

返回看下图 41-1.jpg ，还需要完成 Value 到 Coeff 的转换。

在之前的式子中：

$\begin{bmatrix} P(x_0) \\ P(x_1) \\ \vdots \\ P(x_{n-1}) \end{bmatrix}=\begin{bmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\ 1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n-1} &x_{n-1}^2 & \cdots & x_{n-1}^{n-1} \end{bmatrix}\begin{bmatrix} p_0 \\ p_1 \\ \vdots \\ p_{n-1} \end{bmatrix}$

令 $x_k=\omega ^k\quad \mathrm{where}\quad \omega =e^{\frac{2\pi i}{n}}$

$\begin{bmatrix} P(\omega ^0) \\ P(\omega ^1) \\ P(\omega ^2) \\ \vdots \\ P(\omega ^{n-1}) \end{bmatrix}=\begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega & \omega ^2 & \cdots & \omega ^{n-1} \\ 1 & \omega ^2 & \omega ^4 & \cdots & \omega ^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega ^{n-1} & \omega ^{2(n-1)} & \cdots & \omega ^{(n-1)(n-1)} \end{bmatrix}\begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ \vdots \\ p_{n-1} \end{bmatrix}$

上式中的矩阵被称为 Discrete Fourier Transform (DFT) matrix

$\begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ \vdots \\ p_{n-1} \end{bmatrix}=\begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega & \omega ^2 & \cdots & \omega ^{n-1} \\ 1 & \omega ^2 & \omega ^4 & \cdots & \omega ^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega ^{n-1} & \omega ^{2(n-1)} & \cdots & \omega ^{(n-1)(n-1)} \end{bmatrix}^{-1}\begin{bmatrix} P(\omega ^0) \\ P(\omega ^1) \\ P(\omega ^2) \\ \vdots \\ P(\omega ^{n-1}) \end{bmatrix}$

求出矩阵的逆：

$\begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ \vdots \\ p_{n-1} \end{bmatrix}=\frac{1}{n}\begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega ^{-1} & \omega ^{-2} & \cdots & \omega ^{-(n-1)} \\ 1 & \omega ^{-2} & \omega ^{-4} & \cdots & \omega ^{-2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega ^{-(n-1)} & \omega ^{-2(n-1)} & \cdots & \omega ^{-(n-1)(n-1)} \end{bmatrix}\begin{bmatrix} P(\omega ^0) \\ P(\omega ^1) \\ P(\omega ^2) \\ \vdots \\ P(\omega ^{n-1}) \end{bmatrix}$

这个时候简直是 amazing 啊，上面这个矩阵和之前的那个矩阵形式几乎一样，那么我们在代码上只需要少量改动。

Every $\omega$ in original matrix is now $\frac{1}{n}\omega ^{-1}$ .

伪代码：