一道题开一篇文章实在浪费，于是决定以后零零散散做的题就放在这个集子里了。如果数量过多会考虑再开。

JSOI2004 平衡点（模拟退火）

提交入口

https://www.luogu.com.cn/problem/P1337

题目描述

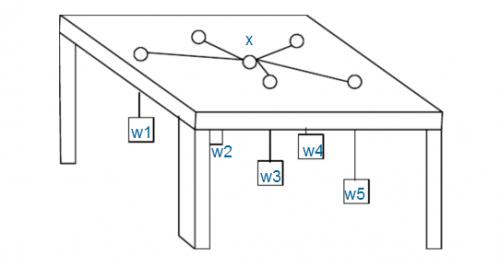
如图，有 $n$ 个重物，每个重物系在一条足够长的绳子上。

每条绳子自上而下穿过桌面上的洞，然后系在一起。图中 $x$ 处就是公共的绳结。假设绳子是完全弹性的（即不会造成能量损失），桌子足够高（重物不会垂到地上），且忽略所有的摩擦，求绳结 $x$ 最终平衡于何处。

注意：桌面上的洞都比绳结 $x$ 小得多，所以即使某个重物特别重，绳结 $x$ 也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。

47-1

输入格式

文件的第一行为一个正整数 $n$（$1\le n\le 1000$），表示重物和洞的数目。

接下来的 $n$ 行，每行是 $3$ 个整数 $x_i, y_i, w_i$，分别表示第 $i$ 个洞的坐标以及第 $i$ 个重物的重量。（$-10000\le x_i,y_i\le10000, 0<w_i\le1000$）

输出格式

你的程序必须输出两个浮点数（保留小数点后三位），分别表示处于最终平衡状态时绳结 $x$ 的横坐标和纵坐标。两个数以一个空格隔开。

样例输入 #1

1
2
3
4
3
0 0 1
0 2 1
1 1 1

样例输出 #1

1
0.577 1.000

分析

待续。先贴代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <bits/stdc++.h>
using namespace std;

const int MAXN =1e4+10;
int n,g[MAXN];
double minlen=DBL_MAX;

struct Point{
    double x, y;
    Point(double a=0.0, double b=0.0):x(a),y(b){}
}P[MAXN];
Point ans;

inline double Sqr(double x){return x*x;}

inline double Rand(){
    return double(rand())/double(RAND_MAX);
}

inline double dis(Point a,Point b){
    return sqrt(Sqr(a.x-b.x)+Sqr(a.y-b.y));
}

bool accept(double delta,double temp){
    return delta<0||Rand()<exp(-delta/temp);
}

double calc(Point origin){
    double len=0;
    for(int i=0;i<n;i++)
        len+=dis(origin,P[i])*g[i];
    if(len<minlen){
        ans=origin;
        minlen=len;
    }
    return len;
}

void SA(Point ans0,double T0,double dec,double end){
    double temp=T0;
    Point nowpos=ans0;
    double nowlen=calc(nowpos);
    
    while(temp>end){
        Point nextpos=Point(nowpos.x+temp*(Rand()*2-1),nowpos.y+temp*(Rand()*2-1));
        double nlen=calc(nextpos);
        if(accept(nlen-nowlen,temp)){
            nowpos=nextpos;
            nowlen=nlen;
        }
        temp*=dec;   //dec为退火系数 
    }
    
    for(int i=0;i<1000;i++){ //精度维护
        Point rnd=Point(ans.x+temp*(Rand()*2-1),ans.y+temp*(Rand()*2-1));
        calc(rnd);
    }
}

int main(){
    scanf("%d",&n);
    Point init;
    for(int i=0;i<n;i++){
        scanf("%lf%lf%d",&P[i].x,&P[i].y,&g[i]);
        init.x+=P[i].x;
        init.y+=P[i].y;
    }
    init.x/=n;
    init.y/=n;
    SA(init,1e5,1-1e-2,1e-3);
    
    printf("%.3f %.3f\n",ans.x,ans.y);
    return 0;
}

有机化学之神偶尔会做作弊（tarjan, lca）

提交入口

https://www.luogu.com.cn/problem/P2783

题意简述

给你一个 $n$ 个点，$m$ 条边的无向图。把图中所有的环变为一个点，求变化后某两个点之间有多少个点。

输入格式

第一行两个整数 $n$，$m$。表示有 $n$ 个点，$m$ 根键。

接下来 $m$ 行每行两个整数 $u$，$v$ 表示 $u$ 号碳和 $v$ 号碳有一根键。

接下来一个整数 $tot$ 表示询问次数。

接下来 $tot$ 行每行两个整数，$a$，$b$ 表示询问的两个碳的编号。

输出格式

共 $tot$ 行，每行一个二进制数，表示答案。

样例输入 #1

1
2
3
4
5
6
3 2
1 2
2 3
2
1 2
2 3

样例输出 #1

1
2
10
10

提示

两个碳不成环。

数据范围及约定

对于 $100\%$ 的数据，$1<n\le10 ^ 4$，$1<m\le5\times 10 ^ 4$。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
#include <cstdio>
#include <cmath>
#include <algorithm>
#define MAX(a,b) ((a)>(b)?(a):(b))
#define MIN(a,b) ((a)<(b)?(a):(b))
using namespace std;

const int maxn=1e4+3;
const int maxm=1e5+3;
// Edge_number in a general graph is twice that of a one-way graph
struct Edge{int v,next;};
Edge edge[maxm],edge2[maxm];
int head[maxn],dfn[maxn],low[maxn],stac[maxn],color[maxn],fa[maxn];
int n,m,tot,num,top,cnt,tot_in_txt,lcafa[maxn][25];
int head2[maxn],tot2,dep[maxn],max0;
bool ins[maxn], vis[maxn];

const int topow[] = {1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192};

inline void rd(int &x){
    int w=x=0;
    char ch=0;
    while(ch<'0'||'9'<ch) w|=(ch=='-'),ch=getchar();
    while('0'<=ch&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();
    x=w?-x:x;
}

inline void addedge(int x,int y){
    edge[++tot].v=y;
    edge[tot].next=head[x];
    head[x]=tot;
}

inline void addedge2(int x,int y){
    edge2[++tot2].v=y;
    edge2[tot2].next=head2[x];
    head2[x]=tot2;
}

void tarjan(int x){
    low[x]=dfn[x]=++num;
    stac[++top]=x; ins[x]=true;
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].v;
        if(!dfn[y]){
            fa[y]=x;
            tarjan(y);
            low[x]=MIN(low[x],low[y]);
        }
        else if(ins[y] && y!=fa[x]){
            low[x]=MIN(low[x],dfn[y]);
        }
    }
    if(dfn[x]==low[x]){
        ++cnt; int y;
        do{
            y=stac[top--]; ins[y]=false;
            color[y]=cnt;
        }while(x!=y);
    }
}

void lcainit(int x){
    vis[x] = true;
    for(int i=1;i<=max0;i++)
        if(lcafa[x][i-1])lcafa[x][i]=lcafa[lcafa[x][i-1]][i-1];
        else break;

    for(int i=head2[x];i;i=edge2[i].next){
        int y=edge2[i].v;
        if(y!=lcafa[x][0]){
            lcafa[y][0]=x;
            dep[y]=dep[x]+1;
            if(!vis[y]) lcainit(y);
        }
    }
}

inline int lca(int u,int v){
    if(dep[u]<dep[v])swap(u,v);
    int delta=dep[u]-dep[v];
    for(int x=0;x<=max0;x++)
        if((1<<x)&delta)u=lcafa[u][x];
    if(u==v)return u;
    for(int x=max0;x>=0;x--)
        if(lcafa[u][x]!=lcafa[v][x]){
            u=lcafa[u][x];
            v=lcafa[v][x];
        }
    return lcafa[u][0];
}

int main(){
    rd(n); rd(m);
    for(int i=1;i<=m;i++){
        int x,y;
        rd(x); rd(y);
        addedge(x,y);
        addedge(y,x);
    }
    rd(tot_in_txt);

    for(int i=1;i<=n;i++){
        if(!dfn[i])tarjan(i);
    }

    for(int x=1;x<=n;x++){
        for(int i=head[x];i;i=edge[i].next){
            int y=edge[i].v;
            if(color[x]!=color[y]){
                addedge2(color[x], color[y]);
                addedge2(color[y], color[x]);
            }
        }
    }

    max0=(int)(log(cnt)/log(2))+3;
    lcainit(1);

    while(tot_in_txt--){
        int a,b;
        rd(a); rd(b);
        int k = lca(color[a], color[b]);
        int temp = dep[color[a]] + dep[color[b]] - (dep[k]<<1) + 1;

        char ans[15] = "00000000000000";
        for(int i=13; ~i; i--){
            if(temp>=topow[i]){
                ans[13-i] = '1';
                temp -= topow[i];
            }
        }
        int i = 0;
        while(ans[i]=='0') i++;
        for(; i<=13; i++)putchar(ans[i]);
        putchar('\n');
    }

    return 0;
}

yLOI2022 枕万梦（排序）

提交入口

https://www.luogu.com.cn/problem/P9472

题目描述

天亮了，扶苏不敌困意，早早地进入了梦乡。在失去引力的梦里，扶苏遇到了好多串漂浮着的数列，它们的长度都相等，而且都是美妙的等比数列！出于本能，扶苏想要把这些数列按照字典序排序，可是在梦里扶苏失去了思考的能力，请你来帮帮她！

具体地，有 $n$ 个编号从 $1$ 到 $n$ 的数列 $a_1, a_2, \dots a_n$，每个数列的长度均为 $m + 1$。第 $i$ 个数列 $a_i$ 满足递推式 $a_{i,j} = a_{i,j - 1} \times i$，其中 $1 \leq j \leq m$。而扶苏会告诉你每个序列的首项 $a_{i,0}$，你需要帮助她把这些数列按字典序排序。

输入格式

输入的第一行是两个整数，依次表示 $n$ 和 $m$。
接下来 $n$ 行，每行一个整数，第 $i$ 行的整数表示数列 $a_i$ 的首项 $a_{i,0}$。

输出格式

输出一行 $n$ 个整数，第 $i$ 个整数表示字典序第 $i$ 小的数列的编号。

样例 #1

样例输入 #1

1
2
3
2 2
1
2

样例输出 #1

1
1 2

样例 #2

样例输入 #2

1
2
3
2 3
1
-1

样例输出 #2

1
2 1

样例 #3

样例输入 #3

1
2
3
2 2
1
1

样例输出 #3

1
1 2

样例 #4

样例输入 #4

1
见附加文件中的 B4.in

样例输出 #4

1
见附加文件中的 B4.ans

提示

样例 1 解释

共有两个数列，每个数列的长度均为 $2+1=3$。

对第一个数列 $a_1$：

  • 已知其首项 $a_{1,0} = 1$。
  • 根据 $a_{i,j} = a_{i,j - 1} \times i$，取 $i=1,j = 1$ 可以得到 $a_{1,1} = a_{1,0} \times 1 = 1$。
  • 根据 $a_{i,j} = a_{i,j - 1} \times i$，取 $i=1,j = 2$ 可以得到 $a_{1,2} = a_{1,1} \times 1= 1$。

所以数列 $a_1$ 是 $1,1,1$。

对第二个数列 $a_2$：

  • 已知其首项 $a_{2,0} = 2$。
  • 根据 $a_{i,j} = a_{i,j - 1} \times i$，取 $i=2,j = 1$ 可以得到 $a_{2,1} = a_{2,0} \times 2 = 2 \times 2 = 4$。
  • 根据 $a_{i,j} = a_{i,j - 1} \times i$，取 $i=2,j = 2$ 可以得到 $a_{2,2} = a_{2,1} \times 2= 4 \times 2 = 8$。

所以数列 $a_2$ 是 $2,4,8$。

比较字典序可得数列 $a_1$ 是字典序最小的数列。所以输出 $1$。

样例 2 解释

数列 $a_1$ 为 $1,1,1,1$，数列 $a_2$ 为 $-1, -2,-4,-8$。

数据规模与约定
本题共 $10$ 个测试点，各测试点信息如下表：

47-2

特殊约定 A：保证 $a_{i,0}$ 均相等。
特殊约定 B：保证 $a_{i,0}$ 互不相等。

对全部的测试点，保证 $1 \leq n \leq 10^5$，$1 \leq m \leq 10^9$，$1 \leq |a_{i,0}| \leq 10^9$。

提示

对两个数列 $a_i, a_j$，按如下方式比较其字典序：

找到最小的满足 $a_{i,p} \neq a_{j, p}$ 的下标 $p$，比较 $a_{i, p}$ 和 $a_{j, p}$ 的大小：

  • 如果 $a_{i,p} < a_{j, p}$，则称 $a_i$ 的字典序比 $a_j$ 的小。
  • 如果 $a_{i,p} > a_{j, p}$，则称 $a_i$ 的字典序比 $a_j$ 的大。

可以证明，在本题的限制下，这样的 $p$ 一定存在。

分析

要求根据字典序排序。若两个数列第一个元素就不等，便可比较大小；若两个数列第一个元素相等，由数列定义，第二个元素必然不等，于是可比较大小。对于首元素为零的数列，整个数列都是零。由此得到下述做法：

对于两个不等的 $a_{i,0}$ , 升序排序。对于两个相等的 $a_{i,0}$ , 分正负两种情况：若 $a_{i,0}>0$ , 则行数越大，位序靠后；若 $a_{i,0}<0$ , 则行数越大，位序靠前。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <algorithm>
#include <cstdio>
using LL = long long;
using namespace std;

LL n,m;

struct mnode{
    LL mcontent;
    LL mindex;
    bool operator < (const mnode& v)const{
        if(mcontent != v.mcontent)
            return mcontent < v.mcontent;
        else    
            if(mcontent > 0)
                return mindex < v.mindex;
            else 
                return mindex > v.mindex;
    }
}marray[100010];

int main(){
    scanf("%lld%lld",&n,&m);
    for(LL i=1; i<=n; i++){
        LL x; 
        scanf("%lld",&x);
        marray[i].mcontent = x;
        marray[i].mindex = i;
    }

    sort(marray+1, marray+1+n);

    for(LL i=1; i<=n; i++){
        printf("%lld ",marray[i].mindex);
    }

    return 0;
}

平衡二叉树

最近考研应试之余，尝试着用王道的思路手写了平衡二叉树的代码，但是没有完成，只是个半成品。如果之后还记得的话，也许我会完成它？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
#include <cstdio>
#define MAX(a,b) ((a)>(b)?(a):(b))

inline void rd(int &x){
    int w=x=0;
    char ch=0;
    while(ch<'0'||'9'<ch) w|=(ch=='-'),ch=getchar();
    while('0'<=ch&&ch<='9') x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();
    x=w?-x:x;
}

struct avlNode{
    int value;
    int cnt;
    int lsub_h;   //left sub_tree's height
    int rsub_h;
    int lsub_num; //size of leftSubtree, excluding itself
    int rsub_num;
    avlNode *lchild, *rchild, *fa;
};

class avlTree{
public:
    avlTree(){ T = nullptr; }

    avlNode* getRoot(){ return T; }
    
    void insertX(avlNode*& K, int x){
        avlNode* p = bstInsert(K, x, nullptr);
        maintain_balance_insert(p);
    }

    void deleteX(int x){  // assume there is x
        avlNode* p = find_X_delete(T, x);
        p->cnt--;
        if(p->cnt>=1)return;

        if(p->lchild==nullptr&&p->rchild==nullptr){
            if(p==p->fa->lchild)
                p->fa->lchild = nullptr;
            else 
                p->fa->rchild = nullptr;
        }

        else if(p->lchild!=nullptr&&p->rchild==nullptr){ // !
            if(p==p->fa->lchild)
                p->fa->lchild = p->lchild;
            else
                p->fa->rchild = p->lchild;
            p->lchild->fa = p->fa;
        }

        else if(p->lchild==nullptr&&p->rchild!=nullptr){
            if(p==p->fa->lchild)
                p->fa->lchild = p->rchild;
            else
                p->fa->rchild = p->rchild;
            p->rchild->fa = p->fa;
        }

        else {
            avlNode* qwq = maxValue_in_lsubtree(p);
            p->value = qwq->value;
            p->cnt = qwq->cnt;
            p = qwq;
            if(p==p->fa->lchild)
                p->fa->lchild = p->lchild;
            else
                p->fa->rchild = p->lchild;
            p->lchild->fa = p->fa;
        }
        
        maintain_balance_delete(p);
        delete p;
    }
    
    int index_X(int x){
        //find an avlNode whose value is x，return its index
        //at this point, the binary-tree is balanced
        avlNode* p = find_X(T, x);   // O(logN)
        int ans = -1;
        if(p==p->fa->rchild){
            avlNode* G = find_left_daddy(p);
            ans = G->lsub_num + G->rsub_num + G->cnt
                  - p->rsub_num - p->cnt + 1;
                  //+1: the value-x avlNode goes the end
        }
        else if(p==p->fa->lchild){
            avlNode* G = find_right_daddy(p);
            ans = G->fa->lsub_num + G->fa->cnt
                  + p->lsub_num + 1;
        }
        if(ans==-1) printf("No such avlNode.\n");
        return ans;
    }
    
    int findIndex_X(){
        //Query the avlNode whose index is x, return its value
    }
    
    int preX(){}
    
    int afterX(){}

private:
    avlNode* find_X(avlNode* K, int x){
        while(K!=nullptr && x!=K->value){
            if(x<K->value) K=K->lchild;
            else K=K->rchild;
        }
        if(K==nullptr)
            printf("function find_X() failed.\n");
        return K;
    }

    avlNode* find_X_delete(avlNode* K, int x){
        while(K!=nullptr && x!=K->value){
            if(x<K->value){
                K->lsub_num--;
                K=K->lchild;
            }
            else {
                K->rsub_num--;
                K=K->rchild;
            }
        }
        if(K==nullptr)
            printf("function find_X() failed.\n");
        return K;
    }

    avlNode* find_left_daddy(avlNode* p){}

    avlNode* find_right_daddy(avlNode* p){}

    int lsubtree_height(avlNode* x){
        if(x->lsub_h) return x->lsub_h;
        if(x->lchild==nullptr){
            x->lsub_h = 0;
            return x->lsub_h;
        }
        x->lsub_h = MAX(lsubtree_height(x->lchild), 
                        rsubtree_height(x->lchild))+ 1;
        return x->lsub_h;
    }

    int rsubtree_height(avlNode* x){
        if(x->rsub_h) return x->rsub_h;
        if(x->rchild==nullptr){
            x->rsub_h = 0;
            return x->rsub_h;
        }
        x->rsub_h = MAX(lsubtree_height(x->rchild), 
                        rsubtree_height(x->rchild))+ 1;
        return x->rsub_h;
    }

    avlNode* find_Unbalanced_Node(avlNode* p){
        int sub_balance = 0;
        while(sub_balance>=-1&&sub_balance<=1){ //sub_balance = 0,1,-1
            p = p->fa;
            if(p==nullptr) return p;
            p->lsub_h = p->rsub_h = 0; // erase old data
            int lch = lsubtree_height(p);
            int rch = rsubtree_height(p);
            sub_balance = lch-rch;
        }
        return p;
    }

    avlNode* bstInsert(avlNode* K, int x, avlNode* myfa){
        if(K==nullptr){
            K = new avlNode;
            K->value = x;
            K->fa = myfa;
            K->lchild = K->rchild = nullptr;
            return K;
        }
        else if(x==K->value){
            K->cnt++;
            return K;
        }
        else if(x < K->value){
            K->lsub_num++;     // nice code <(ˉ^ˉ)>
            bstInsert(K->lchild, x, K);
        }
        else{
            K->rsub_num++;
            bstInsert(K->rchild, x, K);
        }
    }

    void maintain_balance_insert(avlNode* p){
        avlNode* subroot = find_Unbalanced_Node(p);
        // after find_Unbalanced_Node, lsub_h & rsub_h is updated
        if(subroot->lchild->lsub_h==subroot->lchild->rsub_h+1){
            rightRotation(subroot->lchild);
        }
        else if(subroot->rchild->lsub_h+1==subroot->rchild->rsub_h){
            leftRotation(subroot->rchild);
        }
        else if(subroot->lchild->lsub_h+1==subroot->lchild->rsub_h){
            leftRotation(subroot->lchild->rchild);
            rightRotation(subroot->lchild);
        }
        else if(subroot->rchild->lsub_h==subroot->rchild->rsub_h+1){
            rightRotation(subroot->rchild->lchild);
            leftRotation(subroot->rchild);
        }
    }

    void maintain_balance_delete(avlNode* p){
        // 删除的节点向上计算 balance
        avlNode* subroot = find_Unbalanced_Node(p);
        if(subroot==nullptr) return;
        // to do 
    }

    void leftRotation(avlNode* p){
        avlNode *f = p->fa, *gf = f->fa;
        f->rchild = p->lchild;
        f->rsub_num = p-> lsub_num;
        f->rchild->fa = f;
        p->lchild = f;
        p->lsub_num = f->lsub_num + f->rsub_num + 1;
        f->fa = p;
        if(gf->lchild==f){
            gf->lchild = p;
        }
        else if(gf->rchild==f){
            gf->rchild = p;
        }
        p->fa = gf;
    }

    void rightRotation(avlNode* p){
        avlNode *f = p->fa, *gf = f->fa;
        f->lchild = p->rchild;
        f->lsub_num = p-> rsub_num;
        f->lchild->fa = f;
        p->rchild = f;
        p->rsub_num = f->lsub_num + f->rsub_num + 1;
        f->fa = p;
        if(gf->lchild==f){
            gf->lchild = p;
        }
        else if(gf->rchild==f){
            gf->rchild = p;
        }
        p->fa = gf;
    }

    avlNode* maxValue_in_lsubtree(avlNode* p){}

    avlNode* T;  // root
};

avlTree P3369;
int main(){
    int n; rd(n);
    avlNode* rooT = P3369.getRoot();
    while(n--){
        int opt, x;
        rd(opt); rd(x);
        switch(opt){
            case 1: P3369.insertX(rooT, x); break;
            case 2: P3369.deleteX(x); break;
            case 3: printf("%d\n", P3369.index_X(x)); break;
            case 4: printf("%d\n", P3369.findIndex_X()); break;
            case 5: printf("%d\n", P3369.preX()); break;
            case 6: printf("%d\n", P3369.afterX()); break;
        }
    }
    return 0;
}

5 倍经验日（背包）

题目背景

现在乐斗有活动了！每打一个人可以获得 5 倍经验！absi2011 却无奈的看着那一些比他等级高的好友，想着能否把他们干掉。干掉能拿不少经验的。

题目描述

现在 absi2011 拿出了 $x$ 个迷你装药物（嗑药打人可耻…），准备开始与那些人打了。

由于迷你装药物每个只能用一次，所以 absi2011 要谨慎的使用这些药。悲剧的是，用药量没达到最少打败该人所需的属性药药量，则打这个人必输。例如他用 $2$ 个药去打别人，别人却表明 $3$ 个药才能打过，那么相当于你输了并且这两个属性药浪费了。

现在有 $n$ 个好友，给定失败时可获得的经验、胜利时可获得的经验，打败他至少需要的药量。

要求求出最大经验 $s$，输出 $5s$。

输入格式

第一行两个数，$n$ 和 $x$。

后面 $n$ 行每行三个数，分别表示失败时获得的经验 $\mathit{lose}_i$，胜利时获得的经验 $\mathit{win}_i$ 和打过要至少使用的药数量 $\mathit{use}_i$。

输出格式

一个整数，最多获得的经验的五倍。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
6 8
21 52 1
21 70 5
21 48 2
14 38 3
14 36 1
14 36 2

样例输出 #1

1
1060

提示

【Hint】

五倍经验活动的时候，absi2011 总是吃体力药水而不是这种属性药。

【数据范围】

  • 对于 $10\%$ 的数据，保证 $x=0$。
  • 对于 $30\%$ 的数据，保证 $0\le n\le 10$，$0\le x\le 20$。
  • 对于 $60\%$ 的数据，保证 $0\le n,x\le 100$， $10<lose_i,win_i\le 100$，$0\le use_i\le 5$。
  • 对于 $100\%$ 的数据，保证 $0\le n,x\le 10^3$，$0<lose_i\le win_i\le 10^6$，$0\le use_i\le 10^3$。

【题目来源】

fight.pet.qq.com

absi2011 授权题目

分析

为防止学校自命题出 dp 埋伏一手，还是练两道为妙。

整体思路看起来比较显然，但是特判会有点麻烦。大佬们都是用数组的，我还是老老实实用记忆化搜索。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <cstdio>
#define MAX(a,b) ((a)>(b)?(a):(b))

const int MAXN = 1e3+5;
int f[MAXN][MAXN],lose[MAXN],win[MAXN],use[MAXN];

int dp(int n, int w){
    if(n<=0) return 0;
    if(f[n][w]) return f[n][w];
    if(!use[n]){
        f[n][w] = dp(n-1,w) + win[n];
        return f[n][w];
    }
    if(!w){
        f[n][w] = dp(n-1,0) + lose[n];
        return f[n][w];
    }
    int temp1 = dp(n-1,w) + lose[n];
    int temp2 = (w-use[n]>=0)?(dp(n-1,w-use[n]) + win[n]):0;
    f[n][w] = MAX(temp1, temp2);
    return f[n][w];
}

int main(){
    int n, x;
    scanf("%d%d",&n,&x);
    
    for(int i=1;i<=n;i++){
        scanf("%d%d%d",&lose[i],&win[i],&use[i]);
    }

    printf("%lld",5ll*dp(n,x));
    return 0;
}

后记

不再给出代码，仅给出链接。

https://www.luogu.com.cn/problem/P5507

https://www.luogu.com.cn/problem/P2324