公式在同济高数七版下册第182页。

不详细推导，只作几何直观的展示。

NOTICE： 以下推导中，高阶无穷小忽略没有写出，因为它会在除以$\Delta x$再取极限之后变为$0$.

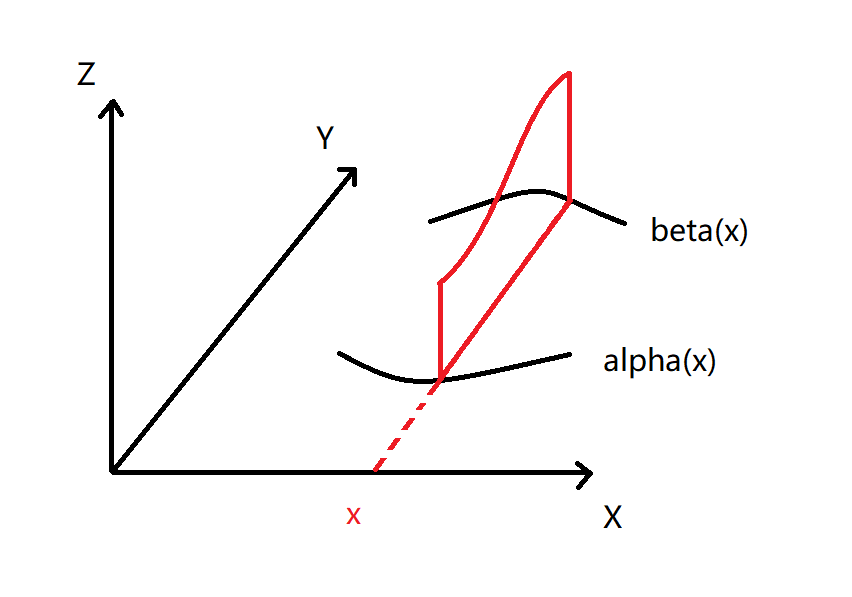
先考虑 $\int_{\alpha (x)}^{\beta (x)} f(x,y)\, \mathrm{d}y$ 的几何直观。现在想象一个三维的曲面$z=f(x,y)$，它也许是这样的（随便画一个）：

matlabpic.png

固定某个选定的$x$值，取曲面$z=f(x,y)$与平面$X=x$的截线：

16-2.png

当$x$固定时，$\int_{\alpha (x)}^{\beta (x)} f(x,y)\, \mathrm{d}y$ 是从$\alpha (x)$到$\beta (x)$对$y$的定积分，在上图中它表示红色曲边梯形的面积。

上图中，红色曲线在曲面$z=f(x,y)$中，清晰起见，曲面$z=f(x,y)$没有画出。$\alpha (x)$和$\beta (x)$是 $x$ 的函数。当$x$变化时，$\alpha (x)$和$\beta (x)$ 的值会相应变化，同时，曲边梯形的形状也会跟着变化。

$\frac{\mathrm{d}}{\mathrm{d}x}\int_{\alpha (x)}^{\beta (x)} f(x,y)\, \mathrm{d}y$ 即曲边梯形面积对$x$的变化率。为此，我们考察当$x$获得一个很小的增量$\Delta x$时，曲边梯形面积将如何变化。

先考虑简单情形: $\alpha (x)$和$\beta (x)$为常函数。在此之前，简单回顾一下微分的几何意义：

16-3.png

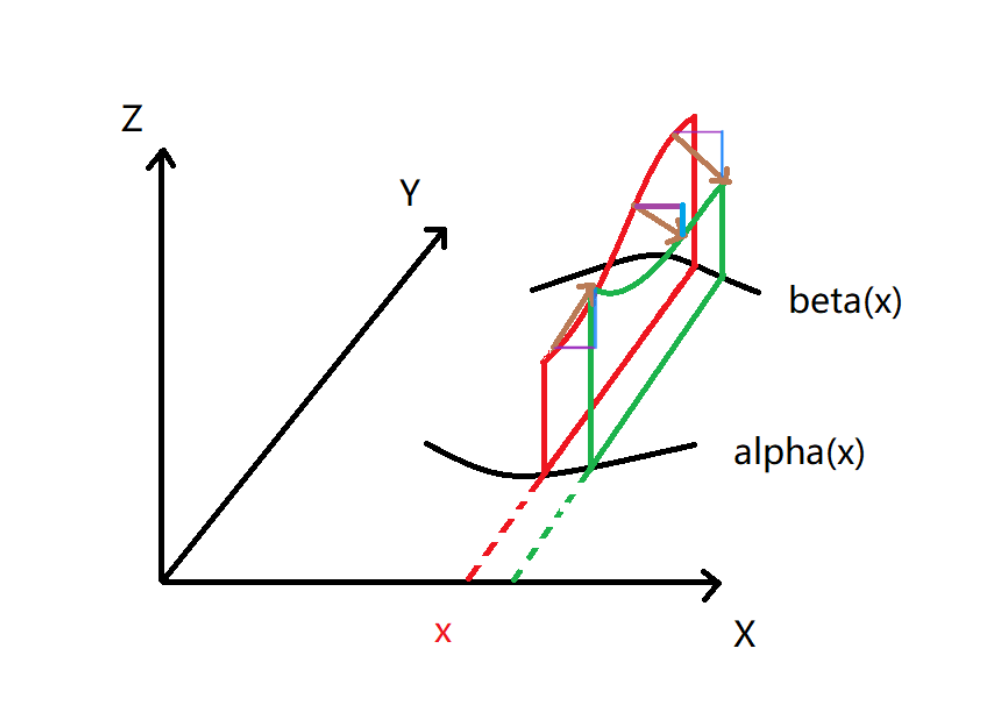
由此得到启发，既然现在是三维的，我们把“在局部范围内用来近似替代非线性函数的线性函数（下图中的蓝色部分）”积起来，就是曲边梯形面积的增量了。

16-4.png

它就是$\Delta x \int_{\alpha (x)}^{\beta (x)} f_{x}^{‘}(x,y)\, \mathrm{d}y$ 。问题还没解决，刚刚只是 $\alpha (x)$和$\beta (x)$ 为常函数的情形，在其他情形中，还需要考虑边界处的增量。注意： 我们考虑的是曲边梯形面积的增量，而不是什么东西的体积的增量。

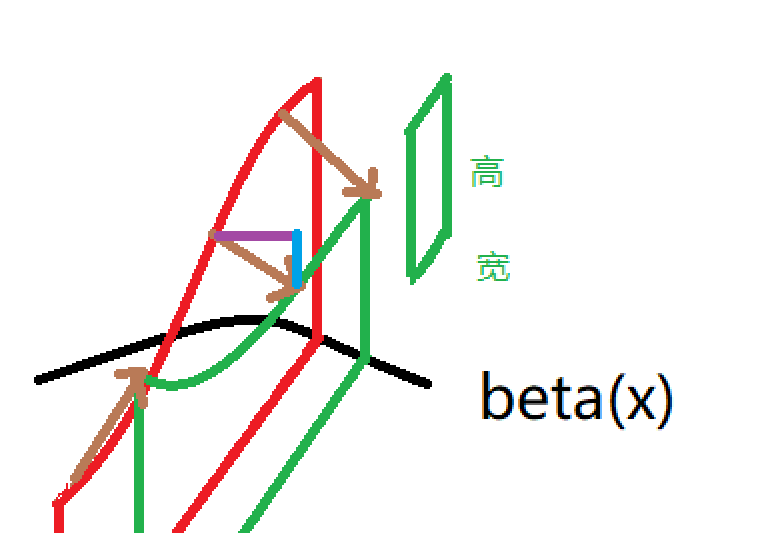
16-5.png

为区分起见，上图将小矩形挪了位置。宽为$\beta ^{‘}(x) \Delta x$，高可用$f[x,\beta (x)]$替代（连续性），因此小矩形的面积为 $f[x,\beta (x)]\beta ^{‘}(x) \Delta x$ 。同理在另一处也有一个小矩形，面积为 $f[x,\alpha (x)]\alpha ^{‘}(x) \Delta x$ ,它们都是我们关注的曲边梯形面积的增量的一部分。因为积分是从$\alpha$积到$\beta$（或者从N-L公式的角度理解），$f[x,\alpha (x)]\alpha ^{‘}(x) \Delta x$ 前面需要加负号，即 $-f[x,\alpha (x)]\alpha ^{‘}(x) \Delta x$ 。

将上述所有的增量（高阶无穷小忽略没有写出）加起来，两边同除$\Delta x$，再令$\Delta x \rightarrow 0$ ，得：