高考数学杂题

以前的笔记。

一些组合题

例一

已知$(1+\dfrac{1}{2}x)^n$展开式的各项依次记为$a_1(x),a_2(x),…,a_{n+1}(x),$设函数$F(x)=\sum\limits_{k=1}^{n+1}ka_k(x)$。求证：$\forall x_1,x_2 \in [0,2],$恒有$|F(x_1)-F(x_2)|\leqslant 2^{n-1}(n+2)-1$。

分析：

答案中给出的解法比较繁琐，其实可以考虑用$\sum\limits$的一些化简技巧和二项式定理。

由题意 :

$$F(x)=\sum\limits_{r=0}^n(r+1)C^r_n(\dfrac{1}{2}\ x)^r$$

这里把$(r+1)$展开 :

$$F(x)=\sum\limits_{r=0}^n[rC^r_n(\dfrac{1}{2}\ x)^r+C^r_n(\dfrac{1}{2}\ x)^r]$$ $$F(x)=\sum\limits_{r=1}^nrC^r_n(\dfrac{1}{2}\ x)^r+\sum\limits_{r=0}^nC^r_n(\dfrac{1}{2}\ x)^r$$

由二项式展开注意到$\sum\limits_{r=0}^nC^r_n(\dfrac{1}{2}\ x)^r=(1+\dfrac{1}{2}\ x)^n$，并且由于$rC^r_n=nC^{r-1}_{n-1}$，我们有:

$$F(x)=n\sum\limits_{r=1}^nC^{r-1}_{n-1}(\dfrac{1}{2}\ x)^r+(1+\dfrac{1}{2}\ x)^n$$

为了配凑得到二项式展开的形式，注意到:

$$\sum\limits_{r=1}^nC^{r-1}_{n-1}(\dfrac{1}{2}\ x)^r=\dfrac{1}{2}\ x\sum\limits_{r-1=0}^{n-1}C^{r-1}_{n-1}(\dfrac{1}{2}\ x)^{r-1}$$

由二项式定理继续化简：

$$F(x)=\dfrac{1}{2}\ xn(1+\dfrac{1}{2}\ x)^{n-1}+(1+\dfrac{1}{2}\ x)^{n}$$

最终得到:

$$F(x)=(1+\dfrac{1}{2}\ x)^{n-1}[\dfrac{1}{2}\ x(n+1)+1]$$

得到$F(x)$的表达式，根据单调性，命题成立。

另外，还有一种方法，不用求公式也可以证出来，但是很难想到。

例二

现有一只青蛙，初始时在$\text{n}$号荷叶上。当祂某一时刻在$\text{k}$号荷叶上时，下一时刻江等概率地随机跳到$1,2,…,k$号荷叶之一上，直至跳到$\text{1}$号荷叶为止。当$\text{n=5}$时，平均一共跳了几次？

分析：

设这个期望为$E(n)$，即，我们期望这个蛙在$n$的时候跳$E(n)$次可以到$1$。

先考虑跳一步会怎么样：显然这只蛙可以以$1/n$的概率跳到$1-n$的任一点。那么，这之后呢？我们设第一步以$1/n$的概率跳到了$k$，之后这只蛙就要再跳$E(k)$次到终点。

得到递归方程：

$$\begin{cases}E(n)=\dfrac{1}{n}(\sum\limits_{r=1}^nE(i)+n) \\E(1)=0\end{cases}$$

代入数据解之即可。

例三

已知$\text{A}$与$\text{B}$是集合$\{1,2,,3,\cdots,100 \}$的两个子集，
满足:$\text{A}$与$\text{B}$的元素个数相同，且$A\bigcap B=\varnothing .$若$n \in A$时，总有$2n+2 \in B.$试问：集合$A\bigcup B$中最多有多少个元素?

分析：

建立一个从$\text{A}$到$\text{B}$的映射:）

$$f:x\rightarrow2x+2$$

因为$\forall n\in A,$都可以通过$f$映射到$B,$并且容易知道这个映射是不会产生冲突的，又因为$A\bigcap B=\varnothing,A,B$元素个数相同。所以$f$建立了一一对应的关系。

首先考虑，最小的元素是放在$A$还是放在$B$？注意到$f$是将小一点的元素变大,所以最小的元素必然放在$A$集合里面。那么这个元素的象自然在$B$里面。

反复进行这样的过程：找出未被标记的最小元素放到$A$里面，这个元素的象放到$B$里面，然后标记这两个元素。

错排问题

例：元旦前夕某宿舍的四位同学各写一张贺卡先集中起来，然后每人从中拿一张别人送出的贺卡，则四张贺卡的不同分配方案有多少种？

分析：

考虑容斥。$\text{PS:}$《容斥原理》

由容斥的思想，多加的减回去，然后又多减了，再加回去…列出式子：

$$A_4^4-A_3^3C_4^1+A_2^2C_4^2-A_1^1C_4^3+A_0^0C_4^4$$

例题解决，考虑更一般的情况：$n$个有序元素，全部改变其位置的排列数是多少？

设$f(n)$表示$n$个元素全部错位的排列数，容斥一下得到：

$$f(n)=\sum\limits_{k=0}^n(-1)^kA_{n-k}^{n-k}C_n^k$$

化简之后就得到了那个公式。

另外，也可以通过动态规划得到递推关系，参考：小学生都能看懂的错排问题解析。不过由递推式得到公式似乎并不容易，wikipedia上有较为详细的推导。

一些几何题

例一

已知直线$y=a$交抛物线$y=x^2$于$\text{A,B}$两点，若该抛物线上存在点$\text{C,}$使得$\angle \text{ACB}$为直角，则实数$a$的取值范围是?

分析：

直角转化为圆相关，注意到二次函数会在远处的导数趋向于$+\infty$，但仅仅是趋向——而圆不同，圆的“左顶点”处是竖直下来的，所以如果$a$很大，绝对是可行的，所以$a$的范围一定是某个数到正无穷，找到这个特殊情况即可。

例二

已知椭圆$\text{C:}\dfrac{x^2}{4}+ \dfrac{y^2}{3}=1$的左右焦点分别为$F_1,F_2,$点$A$在椭圆上且满足$AF_2 \perp F_1F_2$.若$P$是椭圆上的动点，则$\overrightarrow{F_1P}\cdot \overrightarrow{F_2A}$的最大值是？

分析：

善用向量乘法的定义（投影那部分）可以看出答案，很多类似的题目也同理。答案是$\dfrac{3}{2} \sqrt{3}$.

例三

已知$A,B,C,D$四点共面$,BC=2$，$AB^2+AC^2=20,$ $\overrightarrow{CD}=3\overrightarrow{CA},$则$|\overrightarrow{BD}|$的最大值为?

分析：（袋鼠角度）

由余弦定理：$AB^2+AC^2-2AB\cdot ACcosA=4$

所以$AB\cdot CDcosA=24$

${BD}^2=AB^2+\dfrac{4}{9}CD^2+\dfrac{4}{3}BA\cdot CDcosA$

即：$BD^2=AB^2+\dfrac{4}{9}CD^2+32$

又因为$AB^2+\dfrac{1}{9}CD^2=20$

所以$BD^2=52+\dfrac{1}{3}CD^2$

由三角形三边关系：$BD+2\geqslant CD$得：

$$BD+2\geqslant \sqrt{3BD^2-52\cdot 3}$$

化简得：$BD^2-2BD-80\leqslant 0$

得到$BD\in[0,10],$故$BD_{max}=10$。

拓展：事实上可以得到$BD \in [8,10]$。

例四

如果$\text{A}$的座標為$(1,1),F_1$是橢圓$\dfrac{x^2}{9}+\dfrac{y^2}{5}=1$的左焦點，$\text{P}$是橢圓上的動點，則$|PA|+|PF_1|$的最小值為？

分析：

這道簡單題放在這裡給自己提個醒：遇到圓錐曲線題不要一昧想著計算。答案是$6-\sqrt2.$

例五

在平面直角坐标系$xOy$中，圆$\text{C1:}(x-1)^2+y^2=2,$圆$\text{C2:}(x-m)^2+(y+m)^2=m^2,$若圆$\text{C2}$上存在点$P$满足：过点$P$向圆$\text{C1}$作两条切线$PA,PB,$切点为$A,B,\triangle ABP$的面积为$\text{1},$则正数$m$的取值范围是?

分析：

以下是答案的思路。

注意到$\triangle ABP$的面积是定值，从而点$P$的位置应该具有某种确定性，故首先由$\triangle ABP$的面积来确定点$P$所满足的条件，进而江问题转化为圆与圆有公共点的问题来加以处理。

设$P(x,y),$设$PA,PB$的夹角为$2\theta.$

$\triangle ABP$的面积$S=\dfrac{1}{2}PA^2sin2\theta.$

$$S=PA^2\cdot sin\theta \cdot cos\theta$$ $$S=PA^2\cdot \dfrac{\sqrt2}{PC_1}\cdot \dfrac{PA}{PC_1}=1$$ $$\sqrt2 PA^3=PC_1^2=PA^2+2$$ $$\therefore PA=\sqrt2,PC_1=2$$

$\therefore$点$P$在圆$(x-1)^2+y^2=4$上。

根据圆与圆的位置关系可知：

$$|m-2|\leqslant \sqrt{(m-1)^2+m^2}\leqslant m+2$$

解得$1\leqslant m\leqslant 3+2\sqrt3$

矩阵在圆锥曲线中的应用

高二学完矩阵的时候就有这种想法，用矩阵建立一个平面点集到自身的映射，根据我的瞎猜只能方便的处理斜率相关的问题，如若涉及到长度或是角度关系用它好像不行(?)

对于椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1,(a>b>0)$我们采用矩阵$T=\begin{pmatrix}\dfrac{b}{a}&0\\0&1\end{pmatrix}$建立一个平面点集到自身的映射(这里我是受到$hash$技术的启发)。同时注意到我们找到的矩阵不可以将不同的点映射到同一个点，这体现为：这个矩阵必须是可逆的。

显然$T=\begin{pmatrix}\dfrac{b}{a}&0\\0&1\end{pmatrix}$是可逆的。
假设两点$A(x_1,y_1),B(x_2,y_2)$在椭圆上，则$k_{AB}=\dfrac{y_1-y_2}{x_1-x_2}$.

进行变换$T:$ $A->A^{‘},B->B^{‘}$。

$$\begin{pmatrix}\dfrac{b}{a}&0\\0&1\end{pmatrix}A=A'=(\dfrac{bx_1}{a},y_1)$$ $$\begin{pmatrix}\dfrac{b}{a}&0\\0&1\end{pmatrix}B=B'=(\dfrac{bx_2}{a},y_2)$$

于是得到：

$$k_{A'B'}=\dfrac{y_1'-y_2'}{x_1'-x_2'}=\dfrac{y_1-y_2}{\dfrac{bx_1}{a}-\dfrac{bx_2}{a}}=\dfrac{a}{b}k_{AB}$$

找到了这两者之间的关系，就可以很方便地解决一些问题。

例一

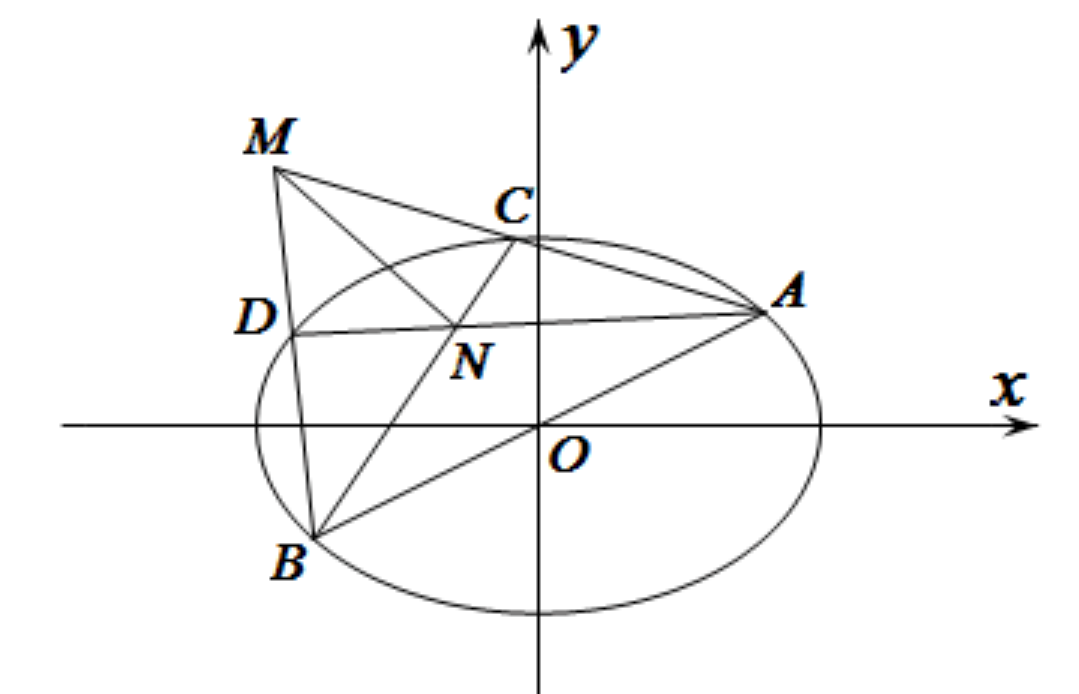
在平面直角坐标系$xOy$中，椭圆$\text{E}:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$的离心率为$\dfrac{\sqrt2}{2},$直线$l:y=\dfrac{1}{2}x$与椭圆$\text{E}$相交于$\text{A,B}$两点，$AB=2 \sqrt5,C,D$是椭圆$\text{E}$上异于$\text{A,B}$的两点，且直线$AC,BD$相交于点$M,$直线$AD,BC$相交于点$N$。
求证$MN$的斜率为定值。

分析：

采用上述矩阵将椭圆变换成圆之后我们发现$M’N’\perp A’B’$那么很容易得到$k_{A’B’}$,然后$k_{M’N’}$也出来了，于是就可以直接得到$k_{MN}$。

Hint：使用矩阵进行映射处理椭圆，有时可以大大简化计算(有时不可以，具体情况具体分析)。特别注意在处理角度或长度问题时，此种方法不再适用。（因为不方便处理，甚至是无法解决，因为对应的方程组不可解(?)），显然，这种方法不能得全分。

一些函数题

例一

已知函数$f(x)=\dfrac{log_2x-1}{log_2x+1},$若$f(x_1)+f(2x_2)=1$(其中$x_1,x_2$均大于$2$)，则$f(x_1x_2)$的最小值为?

分析：这题本不难，但是因为一些奇怪的原因没有做出来。

$\because f(x_1)+f(2x_2)=1$

$\therefore\dfrac{log_2x_1-1}{log_2x_1+1}+\dfrac{log_22x_2-1}{log_22x_2+1}=1$

$\therefore \dfrac{log_2x_1-1}{log_2x_1+1}+\dfrac{log_2x_2}{log_2x_2+2}=1$

化简得$log_2x_2=\dfrac{4}{log_2x_1-1}$

$\therefore log_2(x_1x_2)=log_2x_1+log_2x_2$

$log_2(x_1x_2)=log_2x_1+\dfrac{4}{log_2x_1-1}\geqslant 5$

当且仅当$log_2x_1=3$时等号成立。

$\therefore f(x_1x_2)=\dfrac{log_2(x_1x_2)-1}{log_2(x_1x_2)+1}$

$\therefore f(x_1x_2)=1-\dfrac{2}{log_2(x_1x_2)+1}\geqslant\dfrac{2}{3}$

例二

函数$f(x)=\sqrt{x-3}+ \sqrt{12-3x}$的值域为?

分析(三角换元)：要注意定义域。

$D=[3,4],$则$(x-3) \in[0,1]$

令$x-3=sin^2 \theta,\theta \in [0,\dfrac{\pi}{2}],$则：

$$f(x)=\sqrt{x-3}+\sqrt{3(4-x)}$$ $$f(x)=sin \theta+ \sqrt{3(1-sin^2 \theta)}$$ $$f(x)=sin \theta+ \sqrt{3}cos \theta=2sin( \theta+ \dfrac{ \pi}{3})$$

至此，问题已不难解决。

洛必达法则的应用

洛必达法则1：

若(1)$\lim\limits_{x\to a(\infty)}f(x)=\lim\limits_{x\to a(\infty)}g(x)=0$；(2)在点$a$的某一邻域(不含点$a$)(或$|a|$充分大)内$f’(x),g’(x)$都存在且$g’(x)\ne 0$；(3)$\lim\limits_{x\to a(\infty)}\dfrac{f’(x)}{g’(x)}$存在(或无穷大)，则$\lim\limits_{x\to a(\infty)}\dfrac{f(x)}{g(x)}= \lim\limits_{x\to a(\infty)}\dfrac{f’(x)}{g’(x)}.$

洛必达法则2：

若(1)$\lim\limits_{x\to a(\infty)}f(x)=\lim\limits_{x\to a(\infty)}g(x)=\infty$；(2)在点$a$的某一邻域(不含点$a$)(或$|a|$充分大)内$f’(x),g’(x)$都存在且$g’(x)\ne 0$；(3)$\lim\limits_{x\to a(\infty)}\dfrac{f’(x)}{g’(x)}$存在(或无穷大)，则$\lim\limits_{x\to a(\infty)}\dfrac{f(x)}{g(x)}= \lim\limits_{x\to a(\infty)}\dfrac{f’(x)}{g’(x)}.$

例三

设函数$f(x)=x-\ln(x+\sqrt{1+x^2}).$若$x\geqslant0$时，恒有$f(x)\leqslant ax^3,$试求实数$a$的取值范围。

分析：

求导发现这是一个奇函数，又$f(x)$单调增。猜想$x\to0$时$(ax^3)’\geqslant f’(x).$然后洛必达：

$$3a\geqslant \lim\limits_{\varepsilon\to0}\dfrac{1}{\varepsilon ^2}(1-\dfrac{1}{\sqrt{1+\varepsilon ^2}})$$ $$\lim\limits_{\varepsilon\to0}\dfrac{1}{\varepsilon ^2}(1-\dfrac{1}{\sqrt{1+\varepsilon ^2}})=\dfrac{1}{2}$$ $$\therefore a\geqslant \dfrac{1}{6}$$

这样就避免了分类讨论。

一些不等式

例一

若实数$x,y$满足$2x^2+xy-y^2=1,$则$\dfrac{x-2y}{5x^2-2xy+2y^2}$的最大值为?

分析：

给出的条件中，独立变量有两个，因为用$x$表示$y$或用$y$表示$x$均不方便，可引入第三个变量来表示$x,y$.

首先因式分解，由$2x^2+xy-y^2=1,$得$(2x-y)(x+y)=1,$设$2x-y=t,x+y=\dfrac{1}{t},$其中$t\ne 0.$

解得：

$$\begin{cases}x=\dfrac{1}{3}t+\dfrac{1}{3t}\\y=\dfrac{2}{3t}-\dfrac{1}{3}t\end{cases}$$

現在，已經轉化為一道比較常規的題了。

拓展：试求$5x^2-2xy+2y^2$的最值。(hint:构造齐次式)

Bernoulli不等式

$$(1+x)^n\geqslant 1+nx(x\geqslant -1)$$

可以用数学归纳法证明，或许可以用于放缩。

一些数列题

例一 (2015江苏卷)

设$a_1,a_2,a_3,a_4$是各项为正数且公差为$d(d\ne 0)$的等差数列。问是否存在$a_1,d$使得$a_1,a_2^2,a_3^3,a_4^4$依次构成等比数列?

分析：

本题主要是计算，计算没问题就行。

先假设存在。则$q=$

$$\dfrac{(a_1+d)^2}{a_1}=\dfrac{(a_1+2d)^3}{(a_1+d)^2}=\dfrac{(a_1+3d)^4}{(a_1+2d)^3}$$ $$\therefore (a_1+d)^2(a_1+3d)^4=(a_1+2d)^6$$ $$\therefore d^2+9a_1d+a_1^2=0$$

且$(a_1+d)^2=-7a_1d.$

$$\therefore q=-7d=\dfrac{(a_1+2d)^3}{-7a_1d}$$

$\mathcal{A}:$当$d>0$时，易知$q<0,$不成立。

$\mathcal{B}:$当$d<0$时

$$\because \dfrac{(a_1+d)^2}{a_1}=\dfrac{(a_1+2d)^3}{(a_1+d)^2}$$ $$\therefore d^3=2a_1^3+4a_1d^2$$

显然右式大于零，左式小于零，矛盾。

综上，不存在$a_1,d$使得$a_1,a_2^2,a_3^3,a_4^4$依次构成等比数列。

例二

已知$\{a_n\}$是公差为$d$的等差数列，$\{b_n\}$是公比为$q$的等比数列，$q\ne1 \& q\ne -1,$正整数组$E=(m,p,r)(m<p<r).$

问：若数组$E$中的三个数构成公差大于$1$的等差数列，且$a_m+b_p=a_p+b_r=a_r+b_m$，求$q$的最大值。

分析：

先用通项公式表示$b_1$,设数组$E$的公差为$d’$，然后。。。具体来讲是这样的(年代久远的混乱的草稿中硕果仅存的步骤)：

$$\begin{cases}(p-1)d+b_1q^{r-1}=(r-1)d+b_1q^{m-1}\\(m-1)d+b_1q^{p-1}=(p-1)d+b_1q^{r-1}\end{cases}$$ $$\therefore (r-m)d=b_1(q^{p-1}-q^{m-1})$$ $$\therefore b_1=\dfrac{(r-m)d}{q^{p-1}-q^{m-1}}$$

回代到最上面的那个式子：

$$\dfrac{q^{p-1}-q^{r-1}}{q^{p-1}-q^{m-1}}=\dfrac{p-m}{r-m}$$ $$\because \begin{cases}p-m=d'\\r-m=2d'\end{cases}$$ $$\dfrac{q^{d'}-q^{2d'}}{q^{d'}-1}=\dfrac{d'}{2d'}=\dfrac{1}{2}$$

解得$q^{d’}=-\dfrac{1}{2}$或$q^{d’}=1$（舍）

$$\because d'>1\& d'\in Z$$ $$\therefore d'_{min}=3$$ $$\therefore q_{max}=\sqrt[3]{-\dfrac{1}{2}}$$