人工智能导论

绪论

人工智能程序	通常计算机程序
主要是符号处理	主要是数字处理
启发式搜索	依靠算法
控制结构和知识域相分	信息和控制联结在一起
易于修改、更新和改变	难以修改
允许不正确的答案	要求正确的回答
AI程序：干什么	传统程序：干些什么及如何干

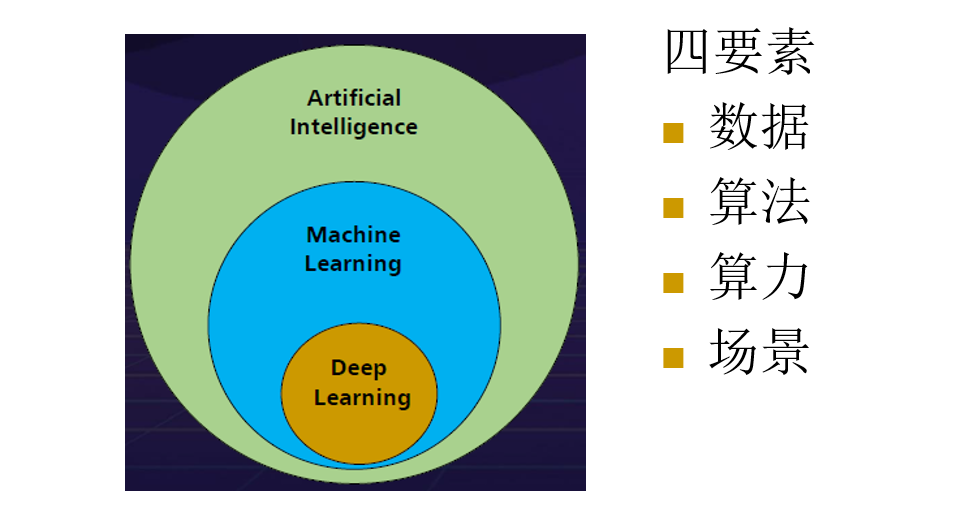
AI 概览：

AI、机器学习、深度学习的关系：

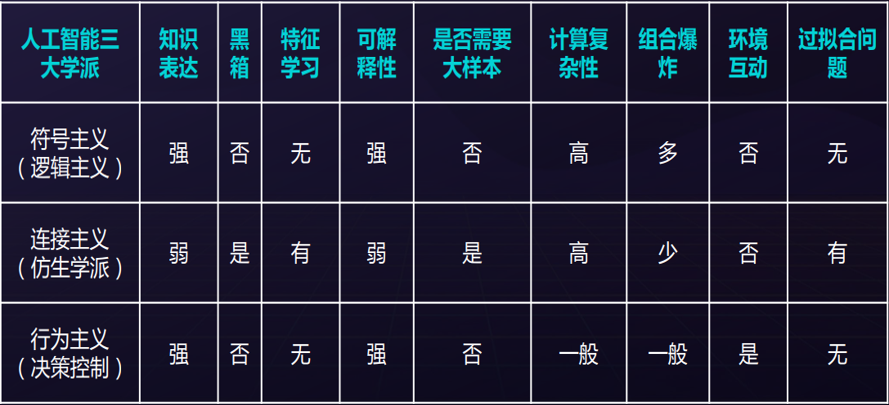
三大学派：符号主义、连接主义、行为主义。

符号主义（逻辑主义、心理学派、计算机学派）

• 原理：物理符号系统假设和有限合理性假设
• 起源：源于数理逻辑
• 基本思想
  • 人的认知基元是符号，智能和知识可用符号表示，认知过程即符号操作过程，擅长抽象思维。
  • 人是一个物理符号系统，计算机也是一个物理符号系统，因此，能用计算机来模拟人的智能行为。
  • 知识是信息的一种形式，是构成智能的基础。人工智能的核心问题是知识表示、知识推理。
  • 
  • 启发式程序、专家系统、知识工程

连接主义（生理学派）

• 原理：神经网络及神经网络间的连接机制和学习算法
• 起源：源于仿生学，特别是人脑模型的研究
• 基本思想
  • 认识的基本元素是神经元，认识过程是大量神经元的并行活动，擅长形象思维。
  • 人脑不同于电脑，并提出连接主义的大脑工作模式，用于取代符号操作的电脑工作模式。
  • 

行为主义（进化主义、控制论学派）

• 原理：控制论及感知-动作型控制系统
• 起源：源于控制论
• 基本思想
  • 智能取决于感知和行动，提出智能行为的“感知-动作”模式。
  • 智能不需要知识、表示和推理；人工智能可以像人类智能一样逐步进化；智能行为只能在现实世界中与周围环境进行交互作用而表现出来。
  • 

三大学派比较：

搜索技术

搜索问题

搜索方式的分类：

• 回溯搜索
• 盲目搜索（深度优先、宽度优先）
• 启发式搜索（A算法→A*算法→A*算法的改进）

传教士和野人问题：
问题可以转化为状态空间的搜索问题：

• 用在河的左岸的传教士人数、野人人数和船的情况表示问题
• 初始状态用三元组表示为（3，3，1）
• 结束状态为（0，0，0）
• 中间状态为（2，2，0）、（3，2，1）、（3，0，0）…… 等，每个三元组对应了三维空间上的一个点

表示方法 — 状态空间表示法

• 状态用来表示系统状态,事实等叙述型知识的一组变量或数组
  $Q = [q_1, q_2, …, q_n]^t$
• 操作是用来表示引起状态变化的过程型知识的一组关系或函数
  $F:\{f_1, f_2, …, f_m\}$
• 状态空间(State Space) 是利用状态变量和操作符号，表示系统或问题的有关知识的符号体系
  四元组 $(S, O, S_0, G):$
  $S$ 状态集合
  $O$ 操作算子集合
  $S_0$ 初始状态，$S_0 \subset S$
  $G$ 目的状态，$G \subset S$，（可是若干具体状态，也可是满足某些性质的路径信息描述）
  从S0结点到G结点的路径被称为求解路径。
• 状态空间的一个解是一有限操作算子序列，它使初始状态转为目标状态
  $S_0 \xrightarrow{O_1} S_1 \xrightarrow{O_2} S_2 \xrightarrow{O_3} \cdots \xrightarrow{O_k} G$
  其中 O1，…，Ok 即为状态空间的一个解（解往往不是唯一的）

如何在一个较大的问题空间中，只搜索较小的范围，就找到问题的解呢？

对于大空间问题，搜索策略要考虑组合爆炸的问题。

盲目搜索，未利用问题的知识，采用固定的方式生成状态的方法。

启发式搜索，利用问题的知识，缩小问题的搜索范围，选择那些最有可能在（最优）解路径上的状态优先搜索，以尽快地找到问题的（最优）解。

回溯策略

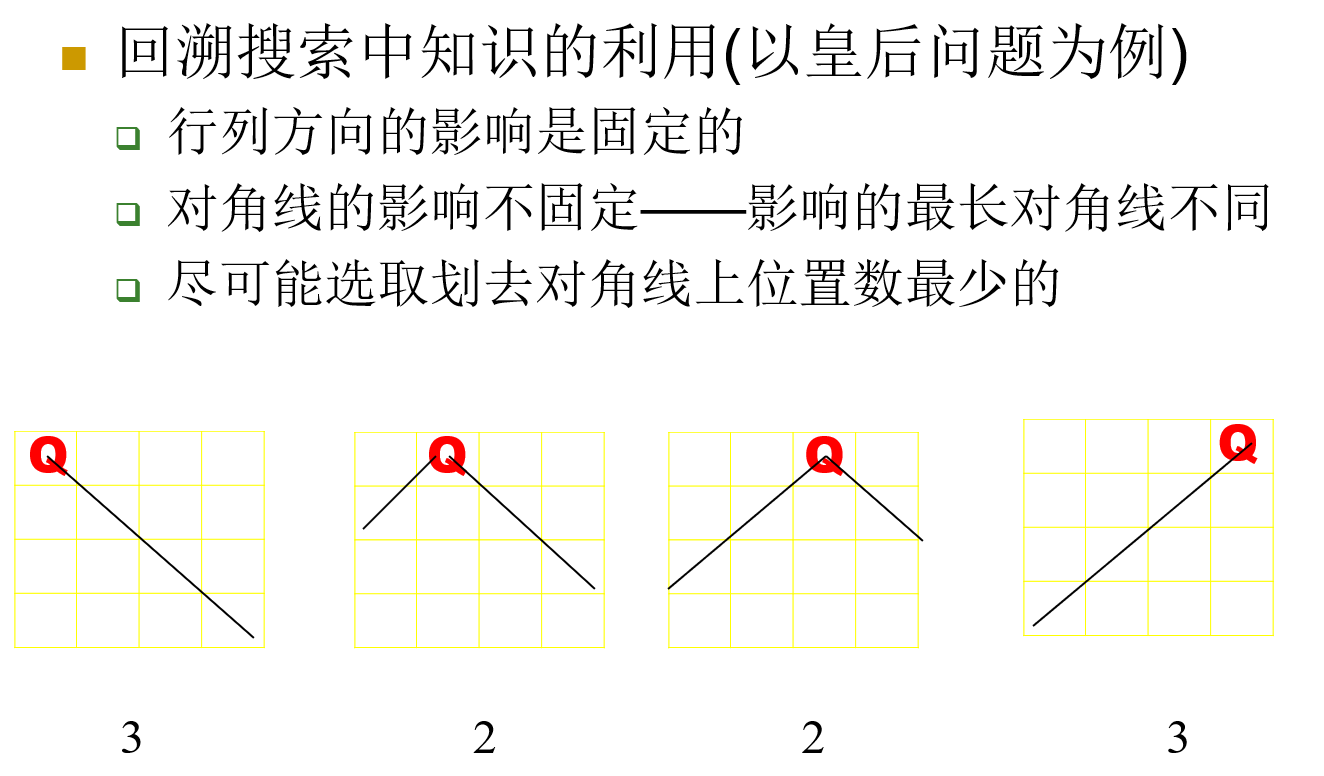
考虑一个经典问题：N 皇后。

我们可以用 dfs 的方法寻找解，但是效率不高。有什么改进的思路吗？

• 回溯有时不是上一步造成的，有可能是更早的那一步造成的——多步回溯
• 找到回溯的原因，在开始就避免回溯——需要引入一些相关信息
• 当然相关信息的引入不应造成搜索负担的巨大加重，否则得不偿失

如此一来，相比于固定排序的搜索树（没有引入知识），动态排序的搜索树（引入知识）的回溯次数大大减少。

回溯搜索算法改进（？）：

• 推广的回溯算法可应用于一般问题的求解，但这两个算法只描述了回溯一层的情况，即第 n 层递归调用失败，则控制退回到（n－1）层
• 深层搜索失败往往在于浅层原因，因此也可以利用启发信息，分析失败的原因，再回溯到合适的层次上，即多层回溯策略，目前已有一些系统使用了这种策略

图搜索策略

问题的引出：

• 回溯搜索：只保留从初始状态到当前状态的一条路径
  • 节省空间，但已搜索部分不能被以后使用
• 图搜索：保留所有已经搜索过的路径
  • 搜索过的路径被保留
  • 利用相关知识，可以进行启发式搜索
• 图搜索策略是实现从一个隐含图中生成出一部分确实含有一个目标节点的显式表示子图的搜索过程

略：一般的图搜索算法、dfs、bfs

启发式图搜索

利用知识来引导搜索，减少搜索范围，降低问题复杂度。

启发信息的强度

• 强：降低搜索量，但可能找不到最优解
• 弱：工作量较大，可能退化为盲目搜索，但找到最优解的概率相对较大

A* 算法

算法流程（如果链接挂了可在 archive.ph 中查看）：

https://paul.pub/a-star-algorithm/

很多介绍 A* 的文章只是讲了 how ，而没有讲 why ，少数讲 why 的博主恐怕在一些细节上也和自己和解了。为此，找一下原始的论文是必要的：

很好论文，解决了我多年的疑惑：

• 如果 h(n) 始终小于等于节点 n 到终点的代价，则 A* 算法保证一定能够找到最短路径。为什么？
• 另外一个小细节：f(n) 是单调不减的，这意味着一旦节点从优先队列中被移出并处理，它的最优路径已经被找到，因为任何从此节点出发的新路径不会比已经找到的路径更优。

练习：

• P5507 机关：A*
• SCOI2005 骑士精神：IDA*

与或图搜索问题

目录：
与或图搜索 2
博弈树搜索（MINI-MAX、α-β剪枝） 10
蒙特卡洛树搜索 25

一些视频资料：

知识表示

概述

选取知识表示的方法的因素：

• 表示范围是否广泛
  • 要求表示内容范围广泛
    • 数理逻辑表示是一种广泛的知识表示办法，如果单纯用数字表示，则范围就有限
• 是否适于推理
  • 人工智能只能处理适合推理的知识表示
    • 数学模型适合推理，普通的数据库只能供浏览检索，但不适合推理
• 是否适于计算机处理
  • 计算机只能处理离散的、量化的字节流。用文字表述的知识和连续形式表示的知识（如微分方程）不适合计算机处理
• 是否有高效的算法
  • 考虑到实用的性能，必须有高效的求解算法，知识表示才有意义
• 能否表示不精确知识
  • 自然界的信息具有先天的模糊性和不精确性，能否表示不精确知识也是考虑的重要因素
  • 许多知识表示方法往往要经过改造，如确定性方法、主观贝叶斯方法等对证据和规则引入了不确定性度量，就是为了表达不精确的知识
• 能否模块化
• 知识和元知识能否用统一的形式表示
  • 知识和元知识是属于不同层次的知识，使用统一的表示方法可以使知识处理简单

• 是否加入启发信息

  • 在已知的前提下，如何最快的推得所需的结论，以及如何才能推得最佳的结论，我们的认识往往是不精确的。因此，往往需要在元知识（控制知识）加入一些控制信息，也就是通常所说的启发信息

• 过程性表示还是说明性表示

  • 说明性知识表示涉及细节少，抽象程度高，因此可靠性好，修改方便，但执行效率低
  • 过程性知识表示的优缺点与说明性知识表示相反
• 表示方法是否自然
  • 一般要尽量在表示方法的自然和使用效率之间取得平衡。例如，对于推理来说，PROLOG 比高级语言如 Visual C++ 自然，但显然牺牲了效率

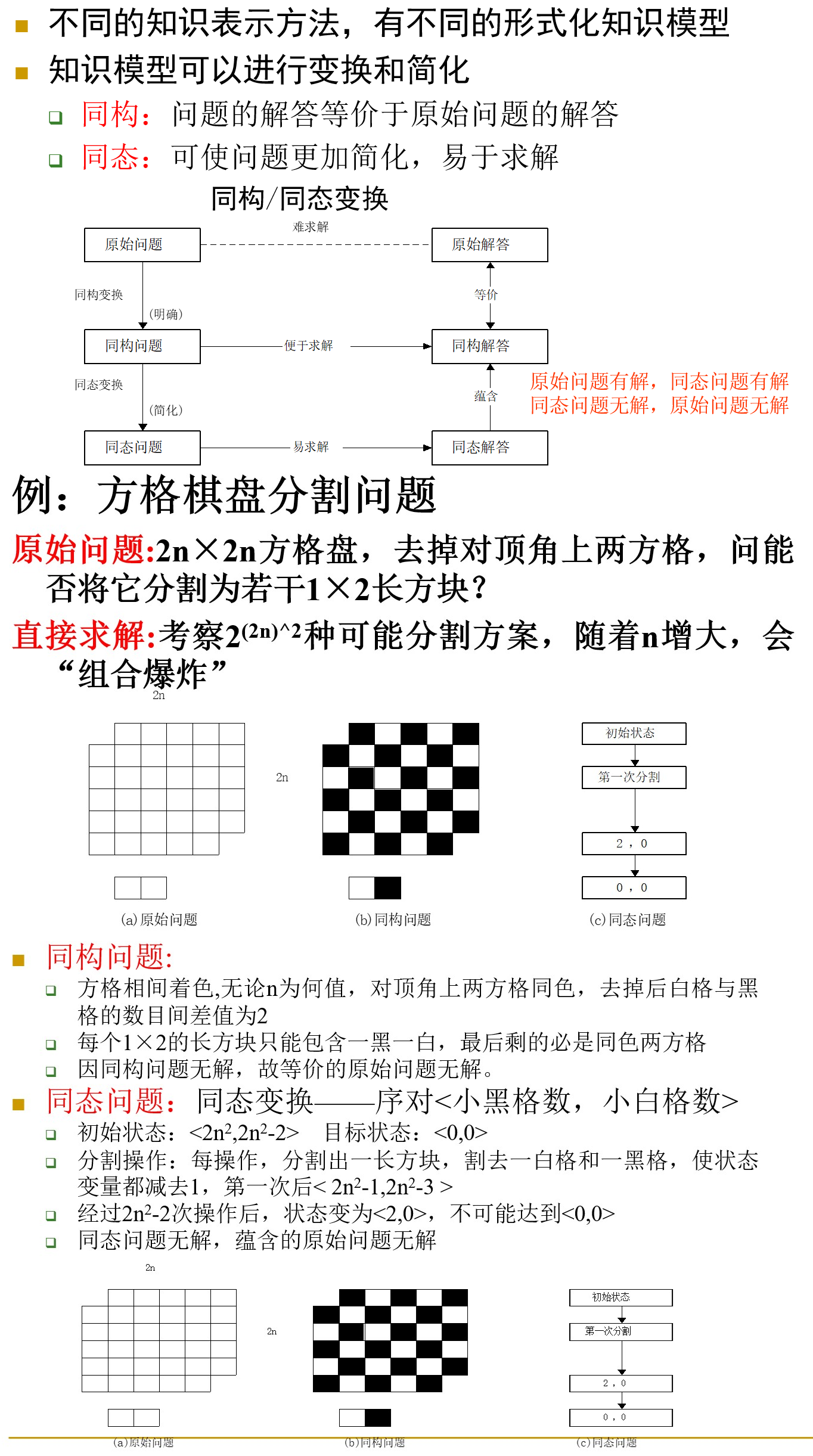
同构与同态：

表示观是对于“什么是表示”这一基本问题的不同理解和采用的方法论，即指导知识表示的思想观点称为表示观。

人工智能领域关于知识表示的观点的争论焦点是常识的处理、表示与推理的关系等问题。

认识论表示观：认为表示是对自然世界的表述，表示自身不显示任何智能行为。其唯一的作用就是携带知识。这意味着表示可以独立于启发式来研究。

本体论（D.Lenta提出）：认为表示是对自然世界的一种近似，它规定了看待自然世界的方式。即一个约定的集合。表示只是描述了关心的一部分，逼真是不可能的。本体论主要解决的问题是：

• 表示需对世界的某个部分给与特别的注意（聚集），而对世界的另外部分衰减，以求达到有效求解。
• 对世界可以采用不同的方式来记述。注重的不是“其语言形式，而是其内容”。此内容不是某些特定领域的特殊的专家知识，而是自然世界中那些具有普通意义的一般知识。
• 计算效率无疑是表示的核心问题之一。即有效地知识组织及与领域有关的启发式知识是其提高计算效率的手段。
• 推理是表示观中不可缺少的一部分。表示研究应与启发式搜索联系起来。认为不考虑推理的纯粹表示是不存在的。

表示方法

逻辑表示法

逻辑表示法的例子：

图片示例：

产生式规则表示法

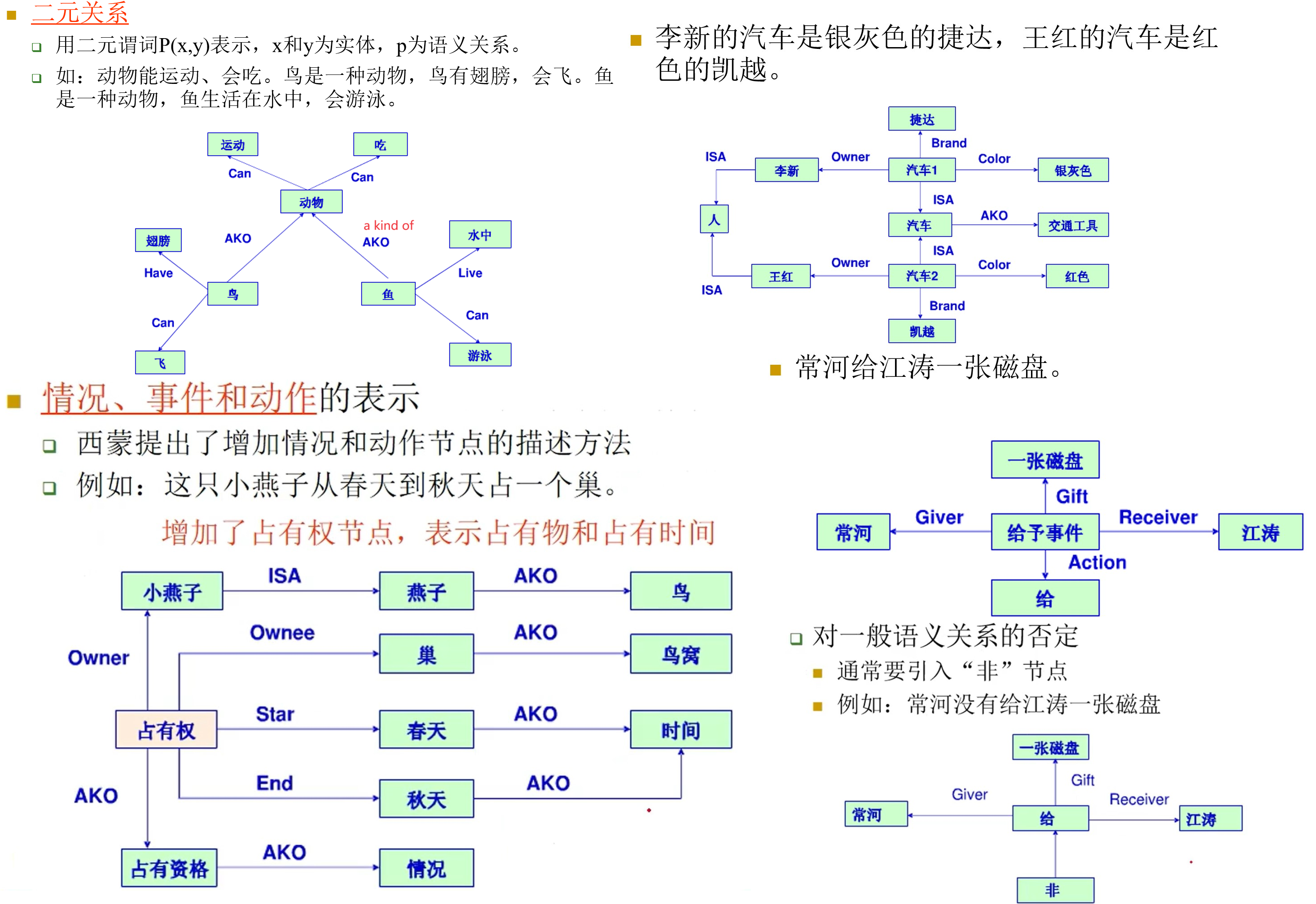
语义网络表示法

语义网络表示法和产生式表示法及谓词逻辑表示法之间有着对应的表示能力。

表示形式：

• 谓词逻辑表示法，Relation（Object1，Object2）
• 语义网络表示法为（Object1，Relation，Object2）
• 语义网络中连接弧上的语义关系对应于逻辑表示法中的谓词关系

一些例子：

语义网络推理，相应的推理方法还不完善。 语义网络的推理过程主要有两种：

• 继承
• 匹配

框架表示法

省流：刻板印象、模板、…

脚本表示法

脚本表示法是框架的特殊形式。

例子，医院的脚本：

开场条件：

1. 病人有病。
2. 病人的病需要找医生诊治。
3. 病人有钱。
4. 病人能够去医院。

角色： 病人、医生、护士。

道具： 医院、挂号室、椅子、桌子、药方、药房、钱、药。

场景：
场景1 进入医院
（1） 人走进医院
（2） 病人挂号
（3） 病人在椅子上坐下等待看病
场景2 看病
（1） 病人进入医生的办公室
（2） 病人向医生所说病状
（3） 医生向病人解释病情
（4） 医生给病人开药方
场景3 交费
（1） 病人到交费处
（2） 病人递交药方
（3） 病人交钱
（4） 病人取回药方及收据
场景4 取药
（1） 病人到药房
（2） 病人递交药方
（3） 病人取药
场景5 离开
（1） 病人离开医院

结果：
1．病人看病了，明白了自己的病是怎么回事
2．病人花了钱，买了药
3．医生付出了劳动
4．医院的药品少了

特点：

• 比语义网络、框架等呆板
• 知识表达范围很窄
• 不适用于表达各种知识，但对实现构思好的特定知识非常有效

知识图谱

什么是知识图谱？

• 知识图谱是 Google 用于增强其搜索引擎功能的知识库（Google 知识图谱，5 亿对象，35 亿事实关系）。
• 从学术的角度，“知识图谱本质上是语义网络（Semantic Network）的知识库”。
• 从实际应用的角度出发，可以简单地把知识图谱理解成多关系图（Multi-relational Graph）。
  • 多关系图一般包含多种类型的节点和多种类型的边
  • 节点：概念、实体
  • 边：关系

知识图谱旨在以结构化的形式描述客观世界中存在的概念、实体及其间的复杂关系。

• 概念：对客观事物的概念化表示，如人、动物、组织机构
• 实体：客观世界中的具体事务，画家达芬奇、作品蒙娜丽莎
• 关系：描述概念、实体之间客观存在的关联

一些具体表现：

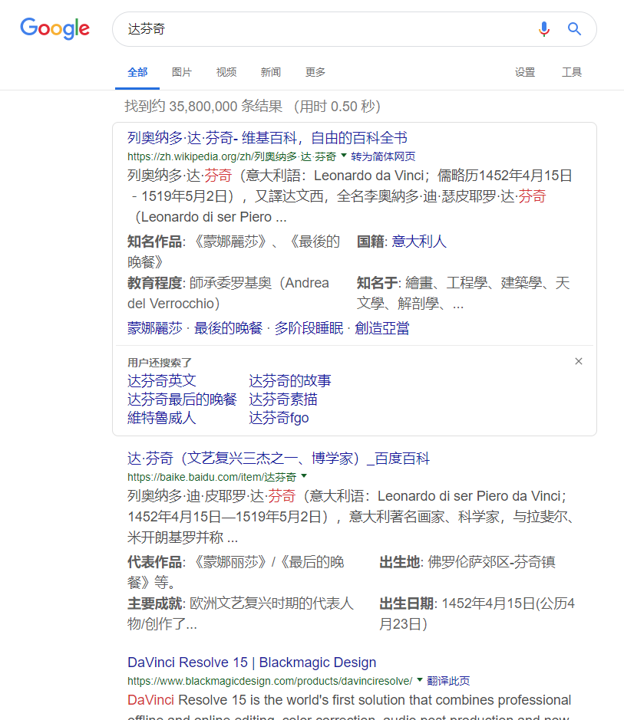
• 传统搜索引擎会返回包含用户搜索关键词的页面
• 知识图谱会返回知识卡片（Knowledge card），为用户查询或返回答案中所包含的概念或实体提供详细的结构化摘要
  

知识图谱经历了由人工和群体智慧构建，到面向互联网利用机器学习和信息抽取技术自动获取的过程。

维基百科是利用群体智能建立的互联网上至今最大的知识资源。

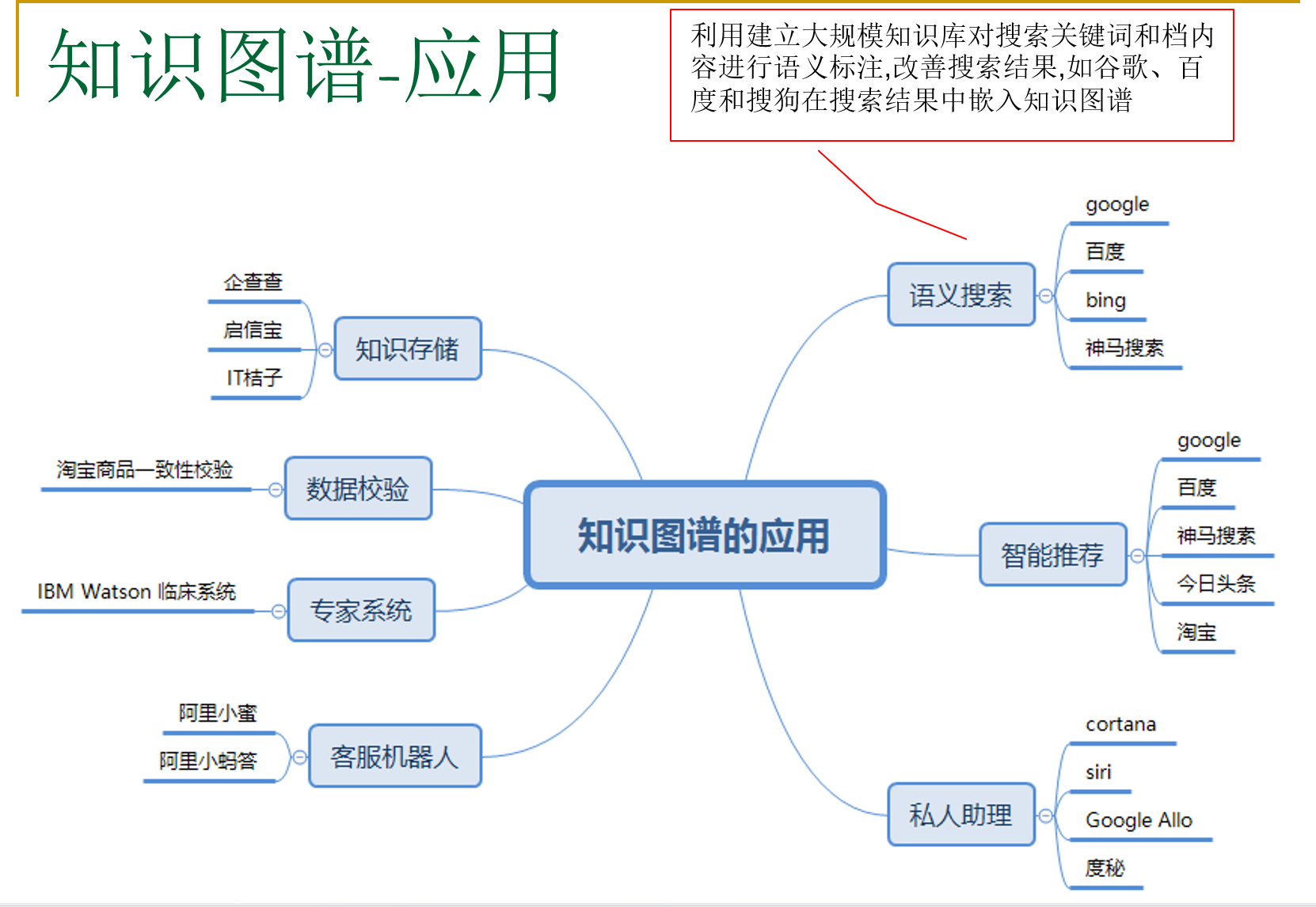
知识图谱的应用：

逻辑推理

概述

演绎推理：

• 从全称判断推出特称判断或单称判断的过程，即从一般到个别的推理
• 演绎推理中最常用的形式是三段论法（大前提、小前提、结论）
• 例如：
  • 所有的推理系统都是智能系统——一般的知识
  • 专家系统是推理系统——个体的判断
  • 所以，专家系统是智能系统——新判断
• 演绎推理没有增加新的知识

归纳推理：

• 从足够多的事例中归纳出一般性结论的推理过程，是一种从个别到一般的推理过程
• 常用的归纳推理有简单枚举法和类比法
  • 枚举法归纳推理是由已观察到的事物都有某属性，而没有观察到相反的事例，从而推出某类事物都有某属性，推理过程为：
    • S1 是 P，S2 是 P，…，Sn 是 P，
      （S1,S2, …,Sn 是 S 类中的个别事物，在枚举中兼容）
      推出 S 都是 P
  • 枚举法归纳推理分完全归纳推理与不完全归纳推理。完全归纳推理是必然性推理，不完全推理得出的结论不具有必然性。
  • 在两个或两类事物在许多属性上都相同的基础上，推出它们在其它属性上也相同，是类比法归纳推理。
  • 类比法归纳可形式化地表示为：
    A 具有属性a,b,c,d,e；B 具有属性a,b,c,d；推出 B 也具有属性e 。
  • 类比法的可靠程度决定于两个或两类事物的相同属性与推出的那个属性之间的相关程度，相关程度越高，则类比法的可靠性就越高
• 归纳推理增加了知识（在机器学习部分称为归纳学习）

默认推理

• 又称缺省推理，是在知识不完全的情况下假设某些条件已经具备，所进行的推理。
• 如：在条件A已成立的情况下，如果没有足够的证据能证明条件B不成立，则就默认B是成立的，并在此默认的前提下进行推理，推导出某个结论。
• 如果到某一时刻发现原先所作的默认不正确，则要撤消所作的默认以及由此默认推出的所有结论，重新按新情况进行推理。

归结原理

Robinson 的归结原理使得自动定理证明得以实现。归结推理方法是机器定理证明的主要方法。

目录
1 命题逻辑的归结法
10 谓词逻辑归结基础（SKolem标准型、子句集）
30 归结原理（置换、归结式、“快乐学生”问题）
50 归结过程的控制策略（删除、支撑集、语义、线性、单元、输入）

不确定性推理

概述

不确定性包括证据的不确定性和知识的不确定性。

证据通常有两类：初始事实、推理过程中产生的中间结果。

证据的不确定性用 C(E) 表示。

在规则中，E 是规则的前提即证据，H 是该规则的结论，也可以是其它规则的证据。

• 规则的不确定性：用一个数值 f(E，H) 表示，称为规则强度。

在不精确推理中，由于知识和证据都具有不确定性，而且知识所要求的不确定性程度与证据实际具有的不确定性程度不一定相同，因而就出现了“怎样才算匹配成功？”的问题。

可以设计一个算法用来计算匹配双方相似的程度，另外再指定一个相似的限度，用来衡量匹配双方相似的程度是否落在指定的限度内。

不确定性的更新和传播：
在推理过程中如何考虑知识不确定性的动态积累和传递？

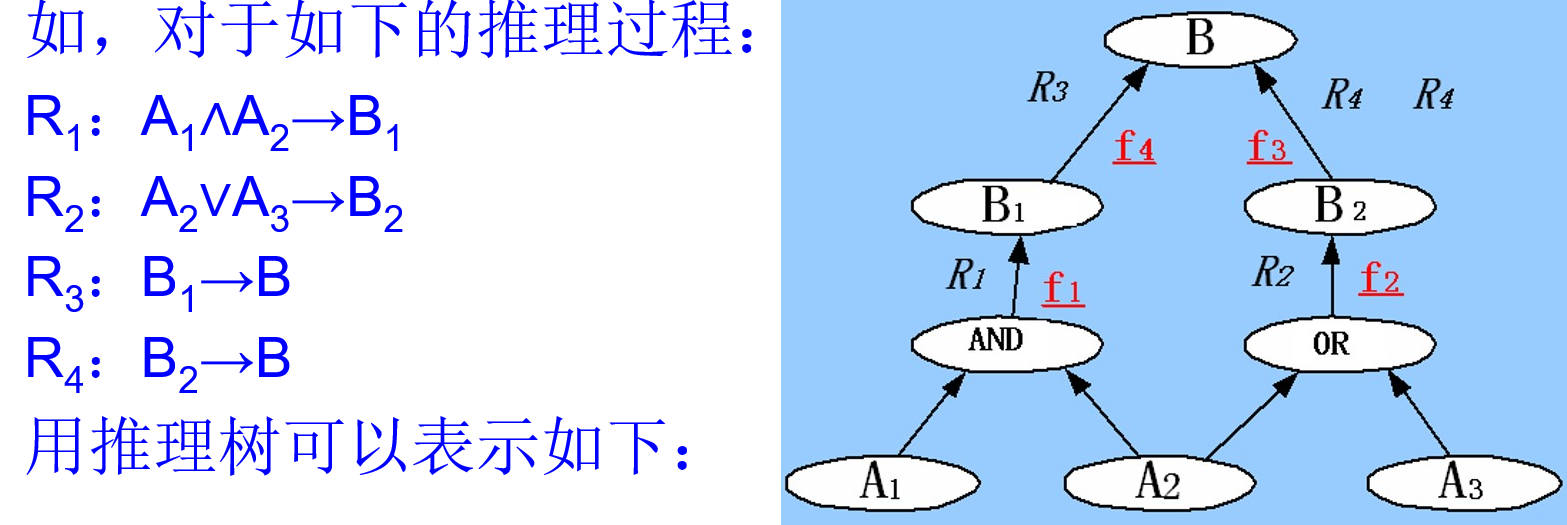
推理树：

确定性方法（可信度方法）

MYCIN 系统研制过程中产生的不确定推理方法（然而这个名字有点误导性）。

规则 A→B，其可信度 CF(B,A)，有 -1 ≤ CF(B, A) ≤ 1

$$CF(B,A)= \begin{cases} \frac{P(B|A)-P(B)}{1-P(B)}, & \text{if }P(B|A) \ge P(B) \\ \frac{P(B|A)-P(B)}{P(B)}, & \text{if } P(B|A) \lt P(B) \end{cases}$$

CF(B, A)表示的意义：证据为真时

• 相对于 P(～B) = 1 - P(B) 来说，A 对 B 为真的支持程度。即 A 发生更支持 B 发生，此时 CF(B, A) ≥ 0
• 相对于 P(B) 来说，A 对 B 为真的不支持程度。即 A 发生不支持 B 发生，此时 CF(B, A) < 0

CF(B, A)的特殊值：

• CF(B, A) = 1，前提真，结论必真
• CF(B, A) = -1，前提真，结论必假
• CF(B, A) = 0 ，前提真假与结论无关

实际应用中 CF(B, A) 的值由专家确定，并不是由P(B|A), P(B)计算得到的。

证据 A 的可信度表示为 CF(A)，-1 ≤ CF( A) ≤ 1 .

特殊值：

• CF(A) = 1， 前提肯定真
• CF(A) = -1， 前提肯定假
• CF(A) = 0， 对前提一无所知
• CF(A) ＞ 0， 表示A以CF(A)程度为真
• CF(A) ＜ 0， 表示A以CF(A)程度为假

实际使用时：

• 初始证据的 CF 值由专家根据经验提供
• 其它证据的 CF 通过规则进行推理计算得到

“与”的计算： A1 ∧ A2 →B
CF(A1 ∧ A2) = min { CF(A1), CF(A2) }

“或”的计算： A1 ∨ A2 →B
CF(A1 ∨ A2) = max { CF(A1), CF(A2) }

“非”的计算：
CF(～A) = -CF(A)

由 A，A →B，求 B：
CF(B) = max{ 0, CF(A) } · CF(B,A)
（ CF(A) ＜ 0 时可以不算，即为“0”）

合成：由 $CF_1(B)$、$CF_2(B)$，求 CF(B)

$$CF(B) = \begin{cases} CF_1(B)+CF_2(B)-CF_1(B)CF_2(B), & CF_1(B) \ge 0, CF_2(B) \ge 0\\ CF_1(B)+CF_2(B)+CF_1(B)CF_2(B), & CF_1(B) \lt 0, CF_2(B) \lt 0\\ CF_1(B)+CF_2(B), & CF_1(B)CF_2(B) \lt 0 \end{cases}$$

注意：以上公式不满足组合交换性，即：计算结果与各条规则采用的先后顺序有关。

MYCIN 规定证据的可信度 CF(A)<0.2 时，就认为该证据引入的规则不可使用。

EMYCIN 系统（MYCIN 发展而成）对 CF1(B) 和 CF2(B) 符号不同时，进行了修正：

$$CF(B) = \begin{cases} CF_1(B)+CF_2(B)-CF_1(B)CF_2(B), & CF_1(B) \ge 0, CF_2(B) \ge 0\\ CF_1(B)+CF_2(B)+CF_1(B)CF_2(B), & CF_1(B) \lt 0, CF_2(B) \lt 0\\ \frac{CF_1(B)+CF_2(B)}{1-\text{min}\{|CF_1(B)|, |CF_2(B)| \}} , & CF_1(B)CF_2(B) \lt 0 \end{cases}$$

结论更新：
已经有一个先验的结论可信度，如何由规则更新这个可信度？

结论更新的三种情况：

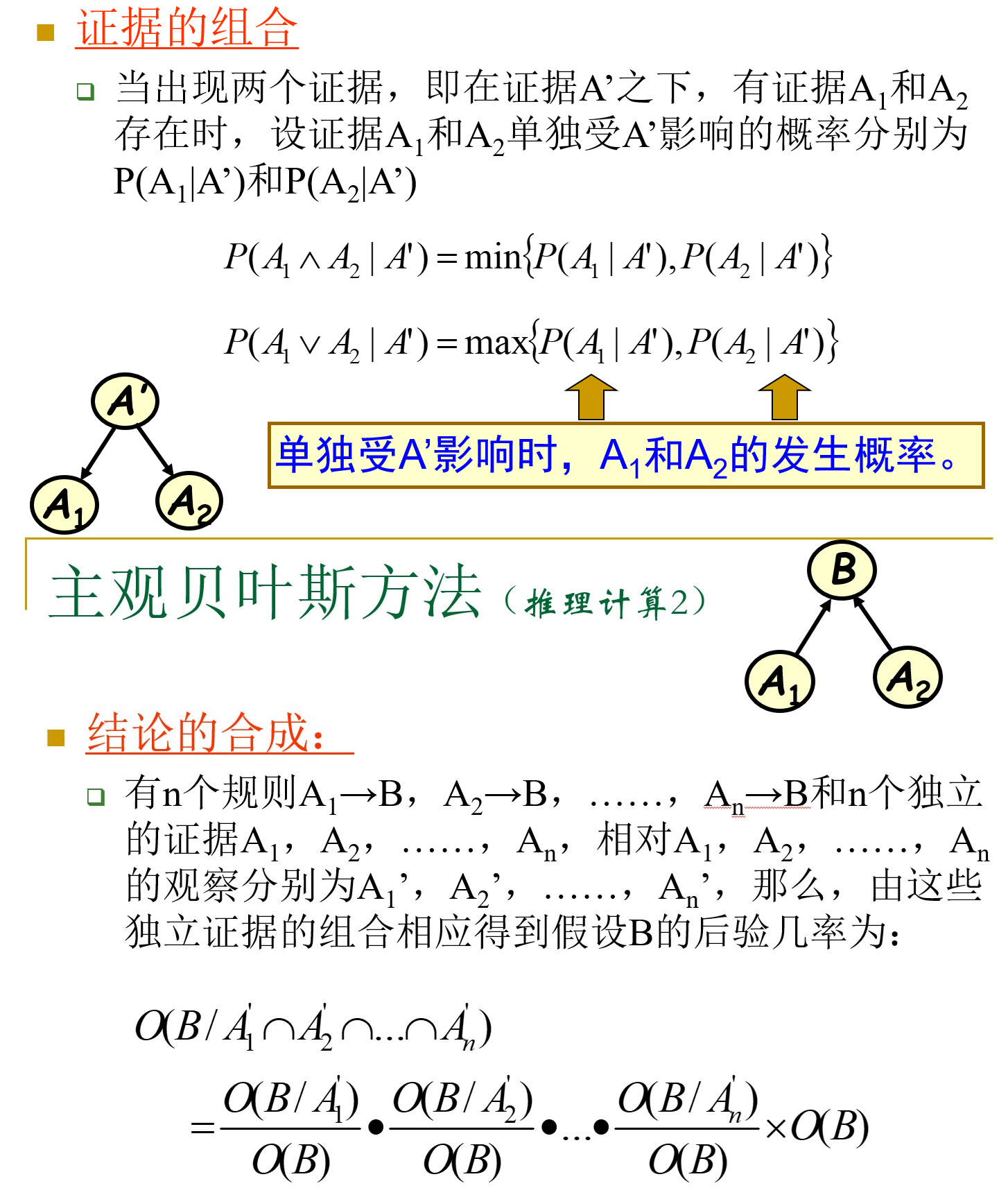
主观 Bayes

该方法首先应用于地矿勘探系统 PROSPECTOR 中。

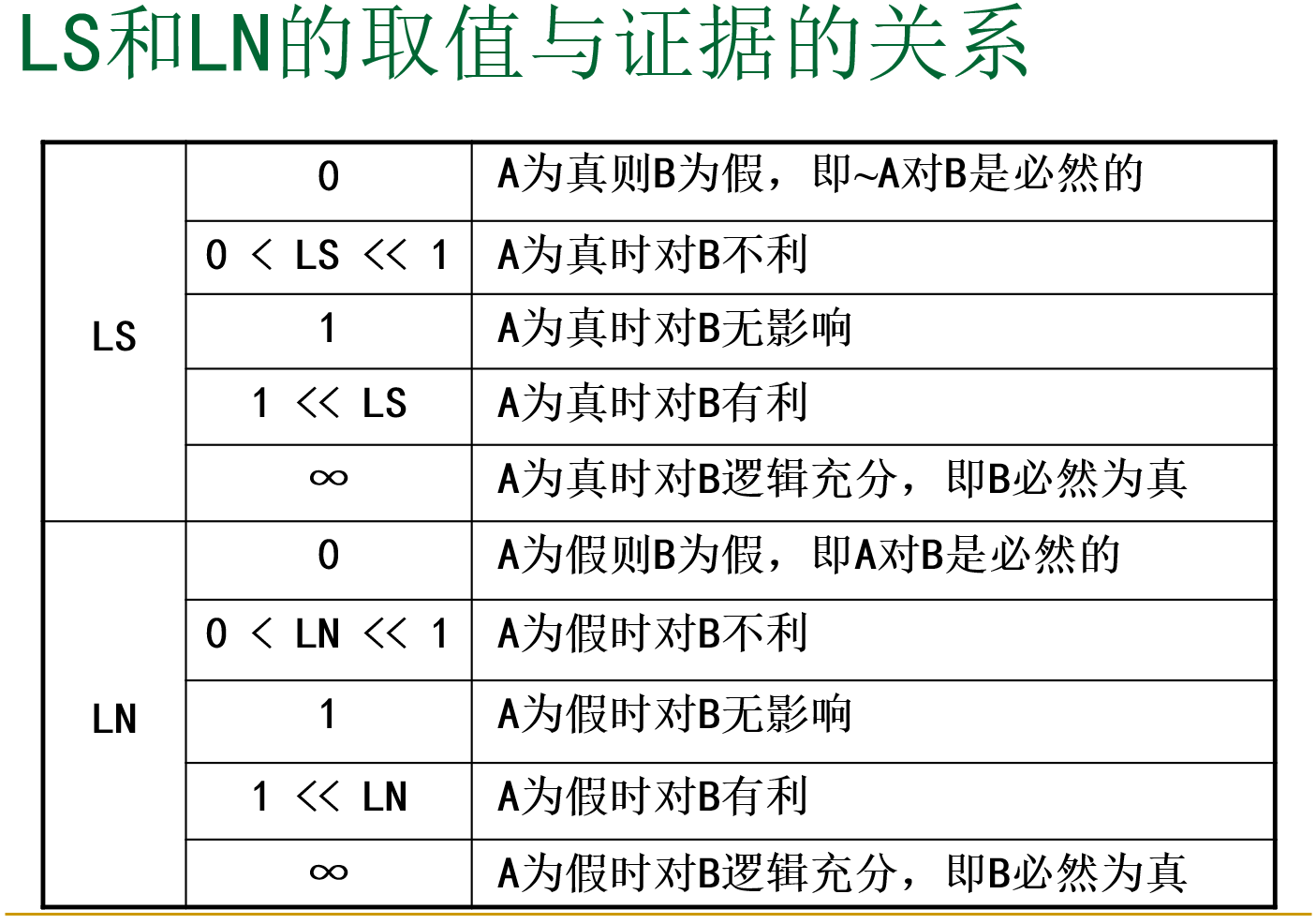
在这种方法中，引入了两个数值 （LS,LN） ：

• 前者体现规则成立的充分性，后者则表现了规则成立的必要性
• LS 表征的是 A 的发生对 B 发生的影响程度
• LN 表征的是 A 的不发生对 B 发生的影响程度
• 实际应用中，采用专家给定的 LS, LN 值

证据的不确定性

几率函数 O(A) 表示证据 A 的不确定性：

$$O(A) = \frac{P(A)}{1-P(A)} = \begin{cases} 0 & \text{A is false} \\ \infty & \text{A is true} \\ (0,\infty) & \text{uncertain} \end{cases}$$

几率函数与概率函数形式不同，但是变化相同：当A为真的程度越大（P(A)越大），几率函数的值也越大。

在推理过程中需要概率函数值时，可用等式：

$$P(A) = \frac{O(A)}{1+O(A)}$$

特殊值：

• P(X) = 0, O(X) = 0
• P(X) = 0.5, O(X) = 1
• P(X) = 1, O(X) = inf

规则的不确定性

规则：A→B

$$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$$ $$P(\lnot B|A) = \frac{P(A|\lnot B)P(\lnot B)}{P(A)}$$

两式相除：

$$\frac{P(B|A)}{P(\lnot B|A)} = \frac{P(A|B)P(B)}{P(A|\lnot B)P(\lnot B)}$$

记：

$$\frac{P(A|B)}{P(A|\lnot B)} = LS$$

又因为：

$$O(B) = \frac{P(B)}{P(\lnot B)} \qquad O(B|A) = \frac{P(B|A)}{P(\lnot B|A)}$$

整理得：

$$O(B|A) = LS \cdot O(B)$$

LS 的含义：

• LS 表示 A 真对 B 的影响程度
• LS = ∞ 时，P(~B|A)=0，P(B|A)=1
• 说明 A 对于 B 是逻辑充分的，即规则成立是充分的
• LS 称作充分似然率因子

$$LS = \frac{O(B|A)}{O(B)} = \frac{P(B|A)/P(\lnot B|A)}{P(B)/P(\lnot B)}$$

LS 表示 A 存在对 B 发生的影响度：

• LS = 1，O(B|A) = O(B)，A 对 B 无影响
• LS > 1，O(B|A) > O(B)，A 支持 B
• LS < 1，O(B|A) < O(B)，A 不支持 B

由类似的推导过程：

$$P(B|\lnot A) = \frac{P(\lnot A|B)P(B)}{P(\lnot A)}$$ $$P(\lnot B|\lnot A) = \frac{P(\lnot A|\lnot B)P(\lnot B)}{P(\lnot A)}$$

两式相除：

$$\frac{P(B|\lnot A)}{P(\lnot B| \lnot A)} = \frac{P(\lnot A|B)P(B)}{P(\lnot A| \lnot B)P(\lnot B)}$$

记：

$$\frac{P(\lnot A|B)}{P(\lnot A| \lnot B)} = LN$$

又因为：

$$O(B) = \frac{P(B)}{P(\lnot B)} \qquad O(B|\lnot A) = \frac{P(B|\lnot A)}{P(\lnot B|\lnot A)}$$

整理得：

$$O(B|\lnot A) = LN \cdot O(B)$$

LN 的含义：

• LN 表示 A 假(即不存在)对 B 的影响程度
• LN = 0 时，P(B|~A)=0
• 说明 A 对于 B 是逻辑必要的，即规则成立是必要性
• LN 称作必要似然率因子

$$LN = \frac{O(B|\lnot A)}{O(B)} = \frac{P(B|\lnot A)/P(\lnot B|\lnot A)}{P(B)/P(\lnot B)}$$

LN 表示 A 不存在对 B 发生的影响度：

• LN = 1，O(B|~A) = O(B)，~A对B无影响
• LN > 1，O(B|~A) > O(B)，~A支持B
• LN < 1，O(B|~A) < O(B)，~A不支持B

LS、LN 的关系：
LN≥0，LS≥0，且 LN 和 LS 彼此不独立。

简单的验证：

$$LS = \frac{P(A|B)}{P(A|\lnot B)} \qquad LN = \frac{P(\lnot A|B)}{P(\lnot A| \lnot B)}$$

当 LS > 1 时：

$$P(A|B)>P(A|\lnot B)$$

故有：

$$LN = \frac{1-P(A|B)}{1-P(A|\lnot B)}<1$$

事实上，LS 和 LN 必处于下面三种情况之一：

• LS > 1, LN < 1
• LS < 1, LN > 1
• LS = LN = 1

LS、LN 的示例：

“如果有石英矿，则必有钾矿带”。
LS=300, LN=0.2

这意味着：
发现石英矿，对判断发现钾矿带非常有利。而没有发现石英矿，并不暗示一定没有钾矿带。如果 LN << 1，则没有发现石英矿时，强烈暗示钾矿带不存在。

推理计算

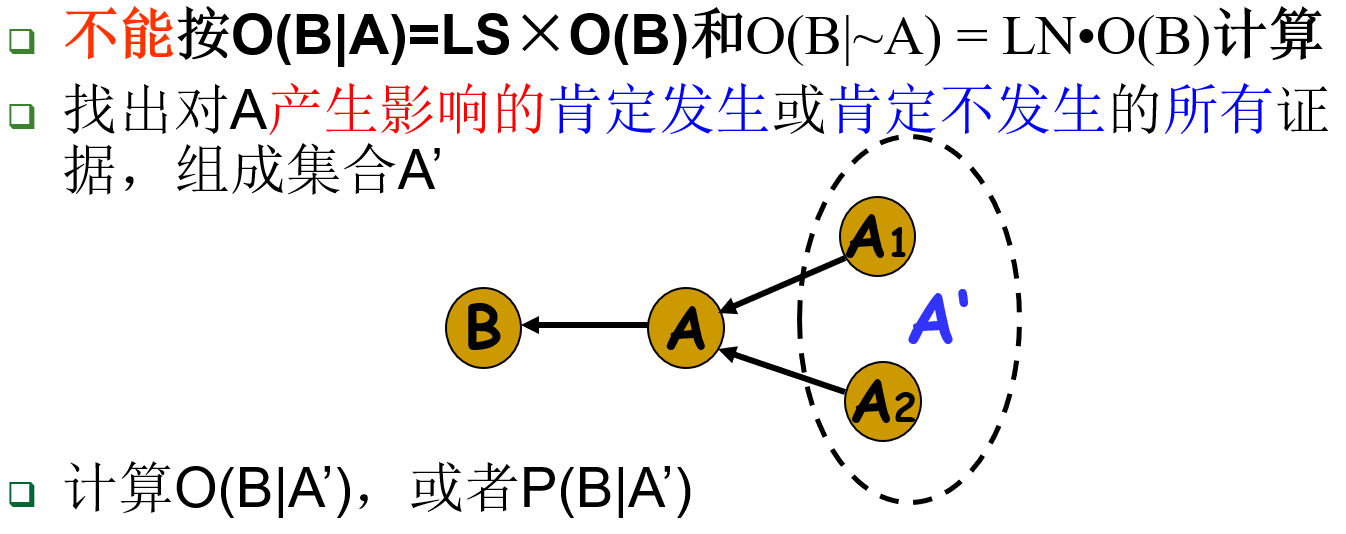
给定先验几率、规则 LS 和 LN，怎样计算后验几率呢？

1） A 必出现或必不出现时，即 P(A)=1 或 P(A)=0 时

$$O(B|A) = LS \cdot O(B)$$ $$O(B|\lnot A) = LN \cdot O(B)$$

2） A 不是必出现或必不出现时，即 P(A)≠1 且 P(A)≠0 时

由全概率公式推得：

$$P(B|A') = P(B|A)P(A|A')+P(B|\lnot A)P(\lnot A|A')$$

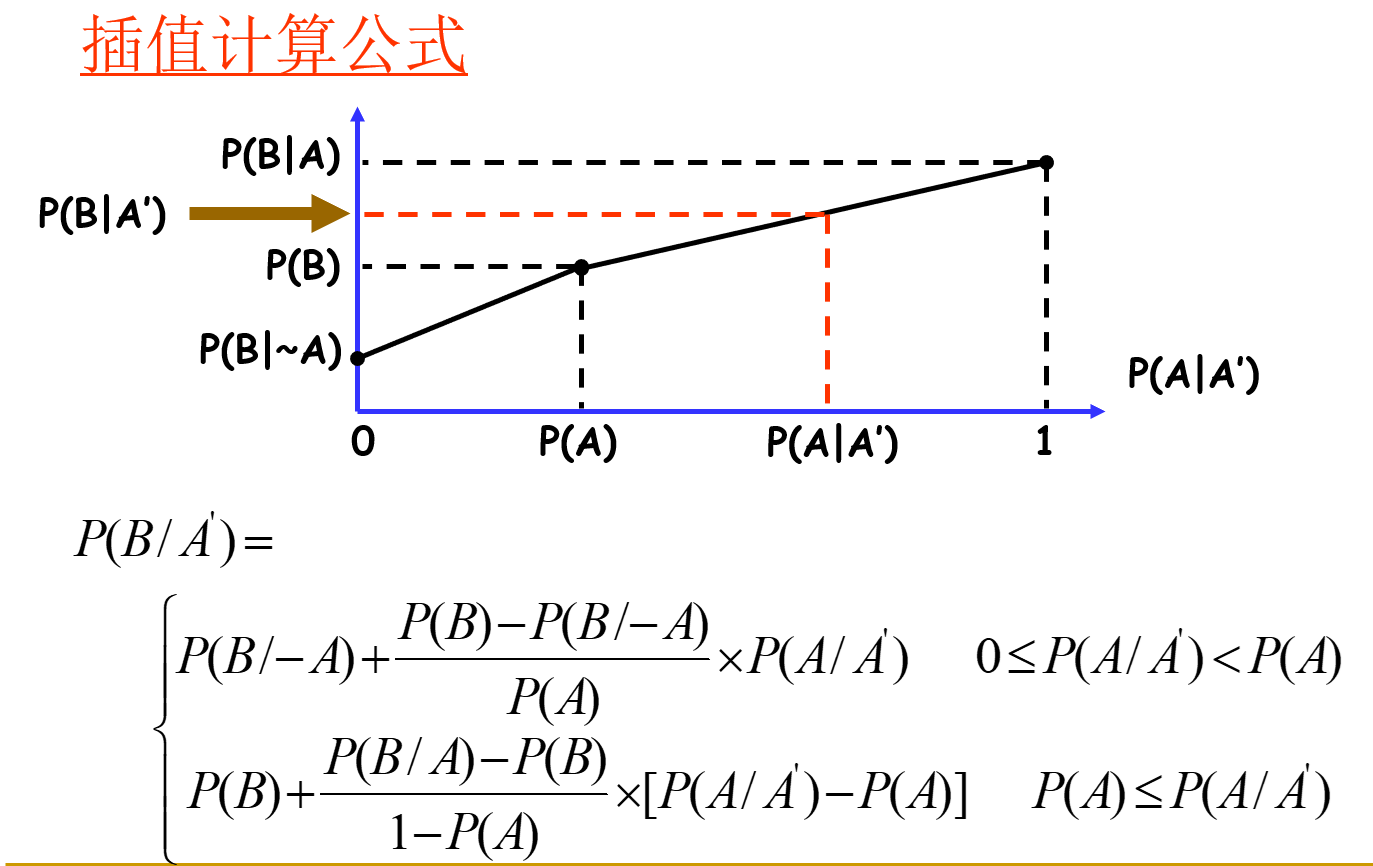
对于上面的式子，先考虑三种特殊情况：

『1』 P(A|A’) = 1 时（证据 A’ 出现，证据 A 必然出现）

$$\begin{aligned} P(B|A') & = P(B|A) \\ & = \frac{P(B|A)}{P(B|A)+P(\lnot B|A)} \\ & = \frac{P(B|A)P(A)}{P(B|A)P(A)+P(\lnot B|A)P(A)} \\ & = \frac{P(AB)}{P(AB)+P(\lnot BA)} \\ & = \frac{P(AB)}{P(AB)+P(A|\lnot B)(1-P(B))} \\ & = \frac{P(A|B)P(B)/P(A|\lnot B)}{P(A|B)P(B)/P(A|\lnot B)+1-P(B)} \\ & = \frac{LS \cdot P(B)}{(LS-1) \cdot P(B)+1} \end{aligned}$$

『2』 P(A|A’) = 0 时（证据 A’ 出现，证据 A 必然不出现）

类似地可以得到：

$$P(B|A') = P(B|\lnot A) = \frac{LN \cdot P(B)}{(LN-1) \cdot P(B)+1}$$

『3』 P(A|A’) = P(A) 时

显然有：

$$P(B| A') = P(B)$$

综上『』，得到以下特殊值：

$$P(B| A') = \begin{cases} \frac{LS \cdot P(B)}{(LS-1) \cdot P(B)+1}, & \text {P(A|A')=1} \\ \frac{LN \cdot P(B)}{(LN-1) \cdot P(B)+1}, &\text{P(A|A')=0} \\ P(B), &\text{P(A|A')=P(A)} \end{cases}$$

在其他位置，使用插值计算：

证据的组合、结论的合成：

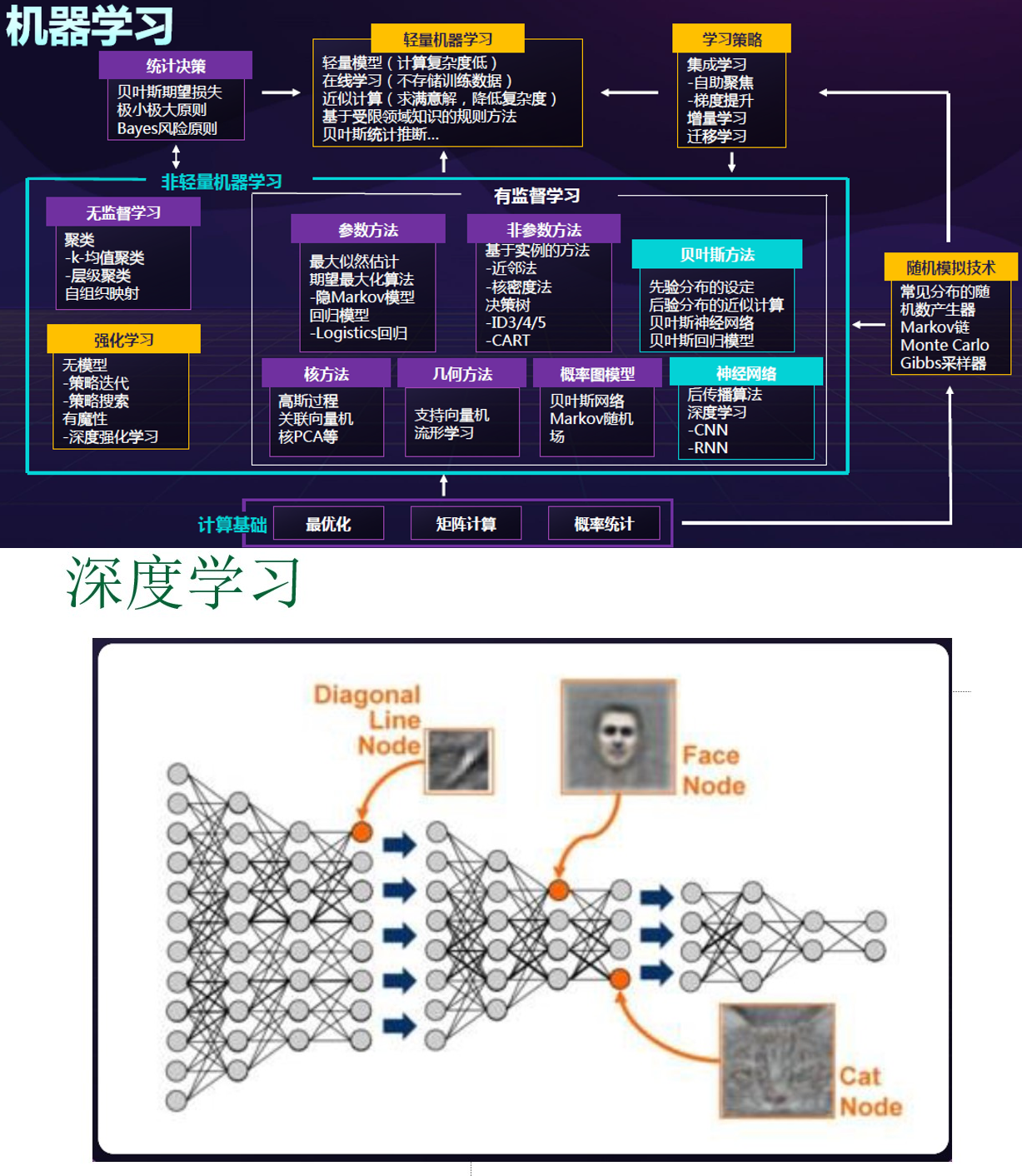
机器学习

概述

机器学习就是让机器（计算机）来模拟和实现人类的学习功能。

基本术语和概念：

• 数据集、训练集、测试集
  
• 泛化能力、误差（训练误差、泛化误差）、欠拟合、过拟合
  • 泛化能力好：对于新的未知数据，也能很好地预测结果。
  • 过拟合：模型可以非常完美地拟合现有数据，但是对于新的数据，拟合效果不好。
• 常见的机器学习任务
  • 分类：逻辑回归
  • 回归：线性回归
• 混淆矩阵
  

机器学习按是否有指导进行分类：

• 监督学习
• 无监督学习
• 半监督学习
• 强化学习

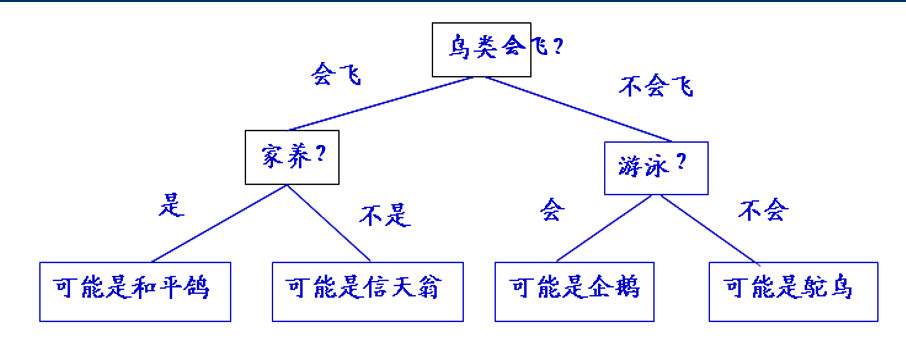
决策树

长这样：

决策树学习的过程实际上是在构造决策树。
学习前提是必须有一组训练实例。
学习结果是根据训练实例构造的决策树。
学习完成后，就可以利用这棵决策树对未知事物进行分类。

可以利用多种算法构造决策树：

• ID 3
• C4.5
• CART
• CHAID

ID3 算法是昆兰（J.R.Quinlan）于 1979 年提出的一种以信息熵的下降速度作为属性选择标准的一种学习算法。其输入是一个用来描述各种已知类别的例子集，学习结果是一棵用于进行分类的决策树。

信息熵（information entropy），是对信息源整体不确定性的度量。

The core idea of information theory is that the “informational value” of a communicated message depends on the degree to which the content of the message is surprising. If a highly likely event occurs, the message carries very little information. On the other hand, if a highly unlikely event occurs, the message is much more informative. For instance, the knowledge that some particular number will not be the winning number of a lottery provides very little information, because any particular chosen number will almost certainly not win. However, knowledge that a particular number will win a lottery has high informational value because it communicates the occurrence of a very low probability event.

The information content, also called the surprisal or self-information, of an event $E$ is a function which increases as the probability $p(E)$ of an event decreases. When $p(E)$ is close to 1, the surprisal of the event is low, but if $p(E)$ is close to 0, the surprisal of the event is high. This relationship is described by the function :

$$\log (\frac{1}{P(E)})$$

Hence, we can define the information, or surprisal, of an event $E$ by :

$$I(E)=−\log _2(p(E))$$

依据 Boltzmann’s H-theorem，香农把随机变量 X 的熵值 $\text{H}$（希腊字母Eta）定义如下：

$$\text{H} (X) = E[I(X)] = E[-\log p(X)]$$

其中 E 为期望函数。

当取自有限的样本时，熵的公式可以表示为：

$$\text{H} (X) = - \sum_{i} P(x_i)\log _b P(x_i)$$

当 b = 2 时，熵的单位是 bit .

加权信息熵：
根据某种方法对样本 S 作一个划分：

$$S_1, S_2, \cdots , S_r$$

则划分后的加权信息熵为：

$$\sum _{t=1}^r \frac{|S_t|}{|S|} \text{H} (S_t)$$

假设 S 中的样本有 m 个属性，其属性集为 X={x1, x2,…,xm}，每个属性 xi 都有不同的取值（xi 取值的个数有 ri 种），根据这个 xi 的取值对样本 S 作划分，则可以记为：

$$\text{H} (S, x_i) = \sum _{t=1}^{r_i} \frac{|S_t|}{|S|} \text{H} (S_t)$$

其中 $S_t$ 为 $x_i = t$ 时的样本子集。

选取不同的属性进行划分，$\text{H} (S, x_i)$ 的值可能不同。记

$$G(S, x_i) = \text{H} (S) - \text{H} (S, x_i)$$

称为信息增益（information gain）。

ID3 算法的学习过程，实际上是一个以整个样本集为根节点，以信息增益最大为原则，选择条件属性进行扩展，逐步构造出决策树的过程。

一个粗略但简单的理解：寻找一个最优的划分。

例子：

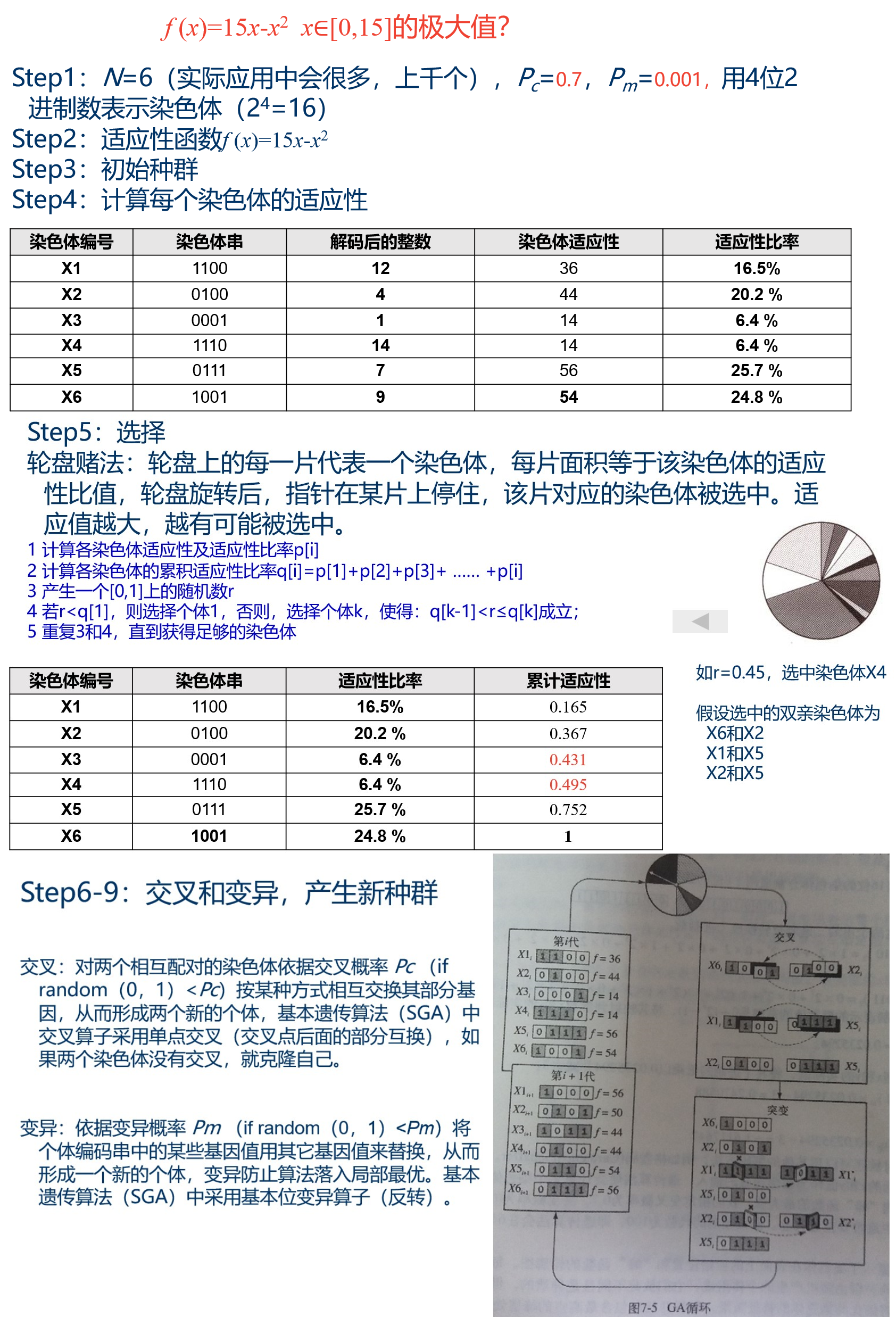
遗传算法

遗传算法（GA）模拟自然界优胜劣汰的进化现象，把搜索空间映射为遗传空间，把可能的解编码成一个向量——染色体，向量的每个元素称为基因。 通过不断计算各染色体的适应值，选择最好的染色体，获得最优解。

例子：

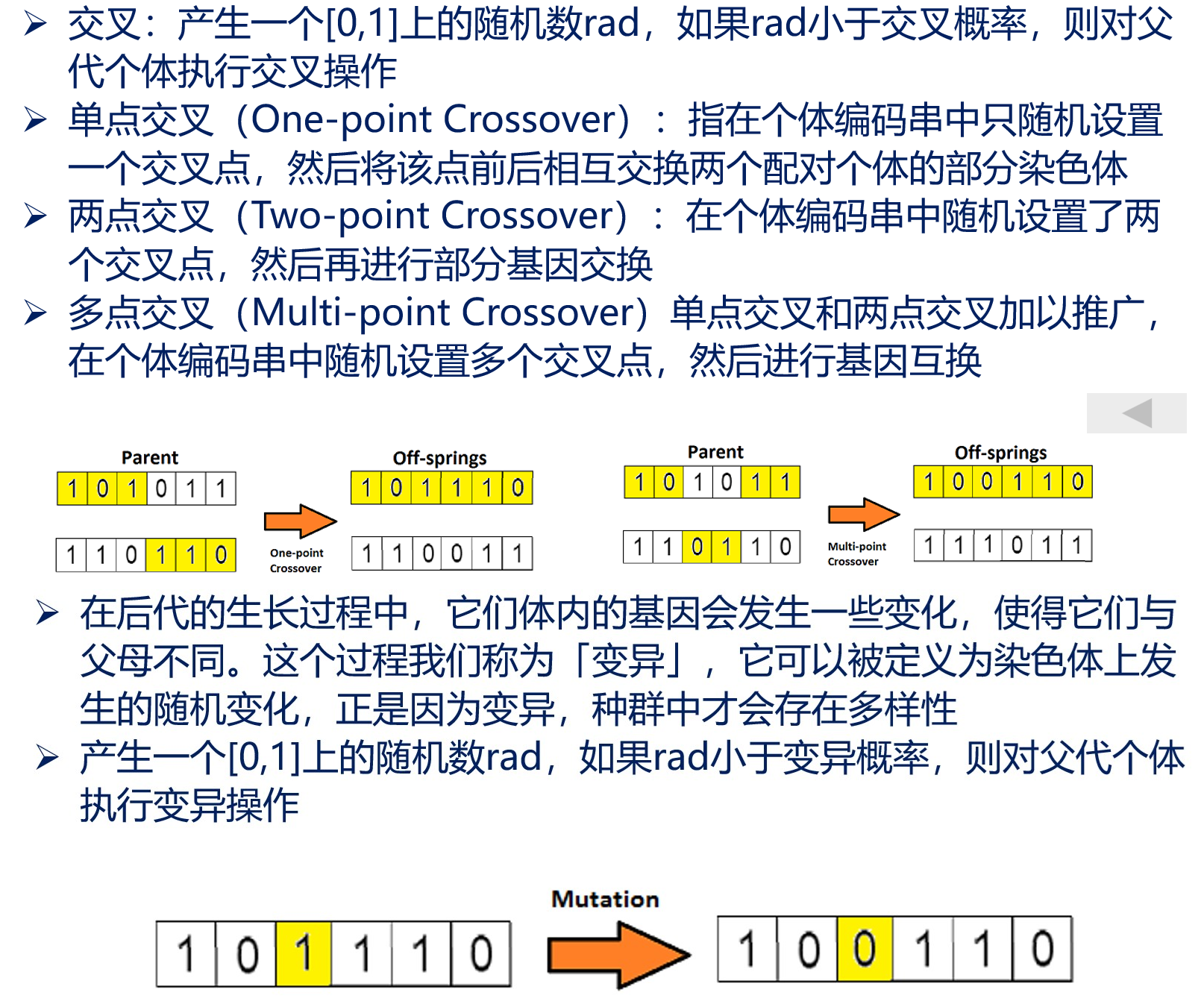
交叉、变异：

遗传算法可用于 TSP 问题，具体细节略。

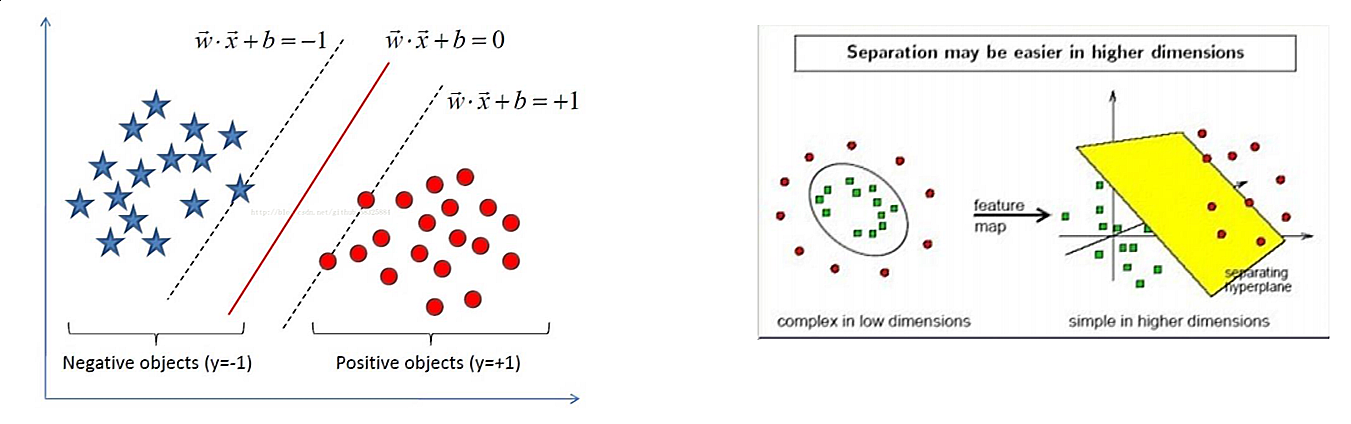
SVM、KNN

支持向量机（support vector machine，SVM）是一个二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器。SVM还包括核技巧，这使它成为本质上的非线性分类器。支持向量机的学习算法是求解凸二次优化的最优化算法。

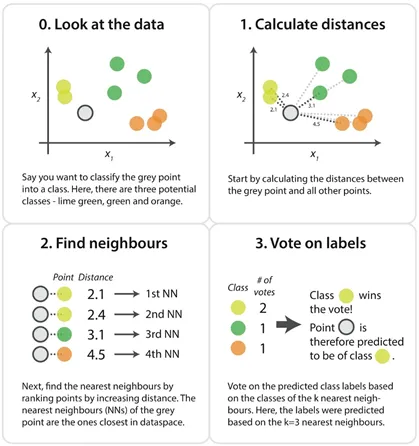
K 最近邻（K-Nearest Neighbor，KNN）分类算法的思路是：如果一个样本在特征空间中的 K 个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。

超参数、验证集

学习模型中一般有两种参数，一种参数是可以从学习中得到，还有一种无法数据里面得到，只能靠人的经验来设定，这类参数就叫做超参数。

模型超参数举例：

• 神经网络的学习速率、迭代次数、批次大小、激活函数、神经元的数量
• 支持向量机的 C 和 σ
• K 近邻中的 K

超参数搜索的一般过程：

• 将数据集分成训练集、验证集、测试集。
• 在训练集上根据模型的性能指标对模型参数进行优化。
• 在验证集上根据模型的性能指标对模型超参数进行搜索。
• 在步骤2和步骤3交替迭代进行，最终确定模型的参数和超参数，并在测试集中评价模型的优劣。

超参数搜索算法：网格搜索、随机搜素、智能搜素、…

交叉验证：用来验证分类器的性能的一种统计分析方法，基本思想是把在某种意义下将原始数据进行分组，一部分作为训练集，另一部分作为验证集，首先用训练集对分类器进行训练，再利用验证集来测试训练得到的模型，以此作为评价分类器的性能指标。

k-折交叉验证（K-CV）：

• 将原始数据分成k组（一般是均分）。
• 将每个子集数据分别做一次验证集，其余的k-1组子集数据作为训练集，这样会得到k个模型。
• 用这k个模型最终的验证集的分类准确率的平均数作为此K-CV下分类器的性能指标。

人工神经网络

基本概念

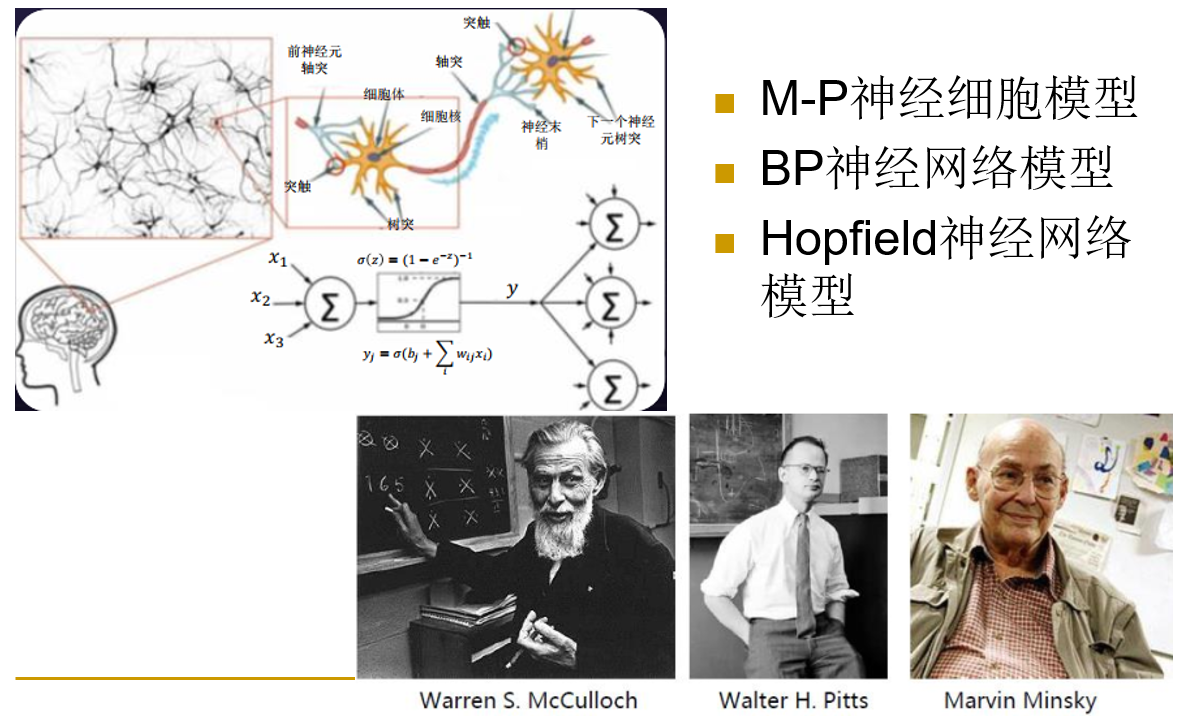
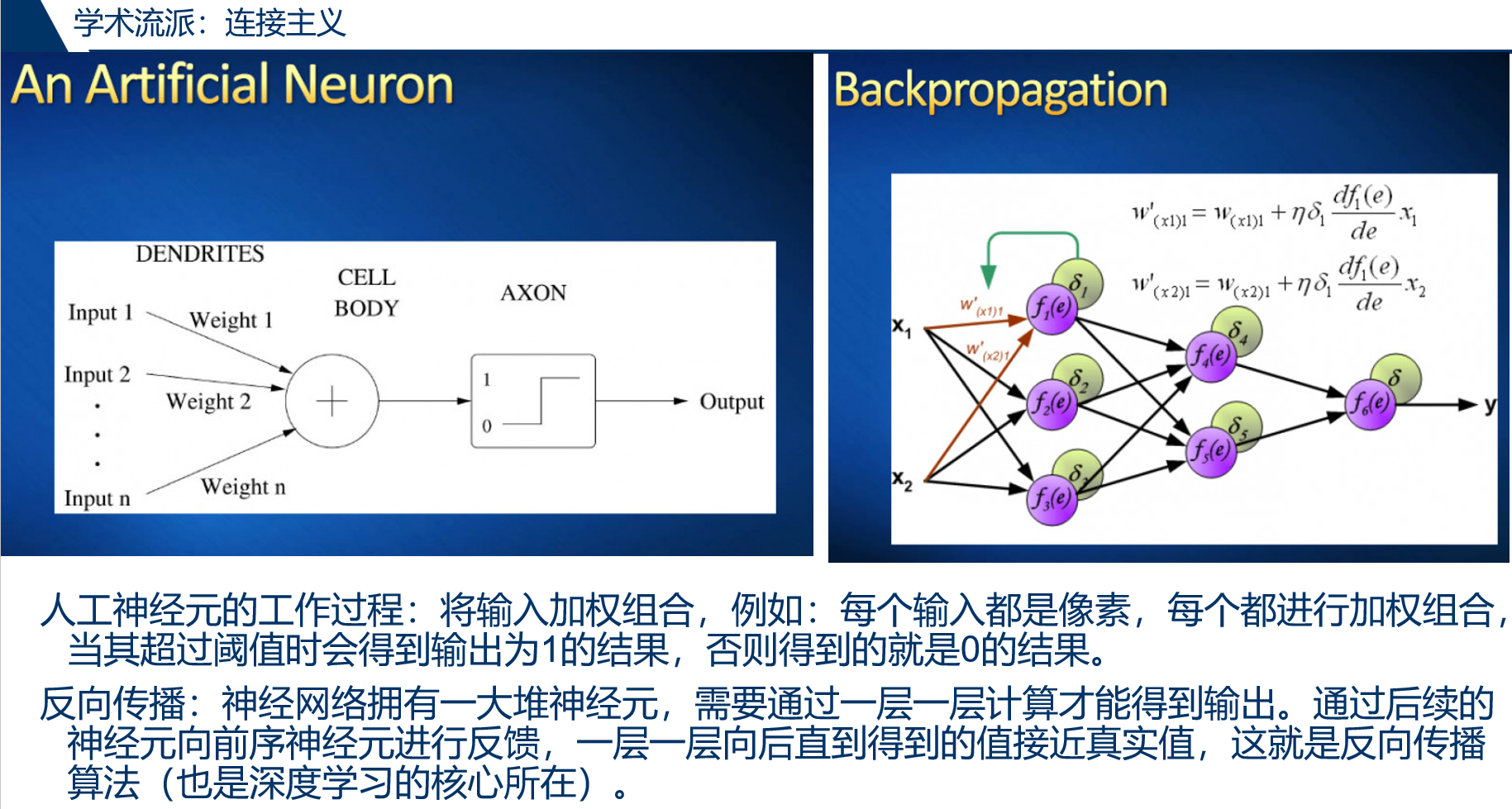
人工神经网络(Artificial Neural Network, ANN)，是一种旨在模仿人脑结构及其功能的信息处理系统。

神经元是神经网络的基本处理单元，科学研究过程中一般是用一个多输入/多输出的非线性器件来模拟生物神经细胞的：

在 M-P 模型中：

$$Y=\text{sign}[\sum_{i=1}^n x_iw_i-\theta]$$

$x_i$ 表示神经元的输入，$w_i$ 表示输入的对应权值，即信号源神经元与该神经元的连接强度，Y 为神经元的输出，$\theta$ 表示神经元的阈值。

深度学习一般指深度神经网络，这里的深度指神经网络的层数较多。

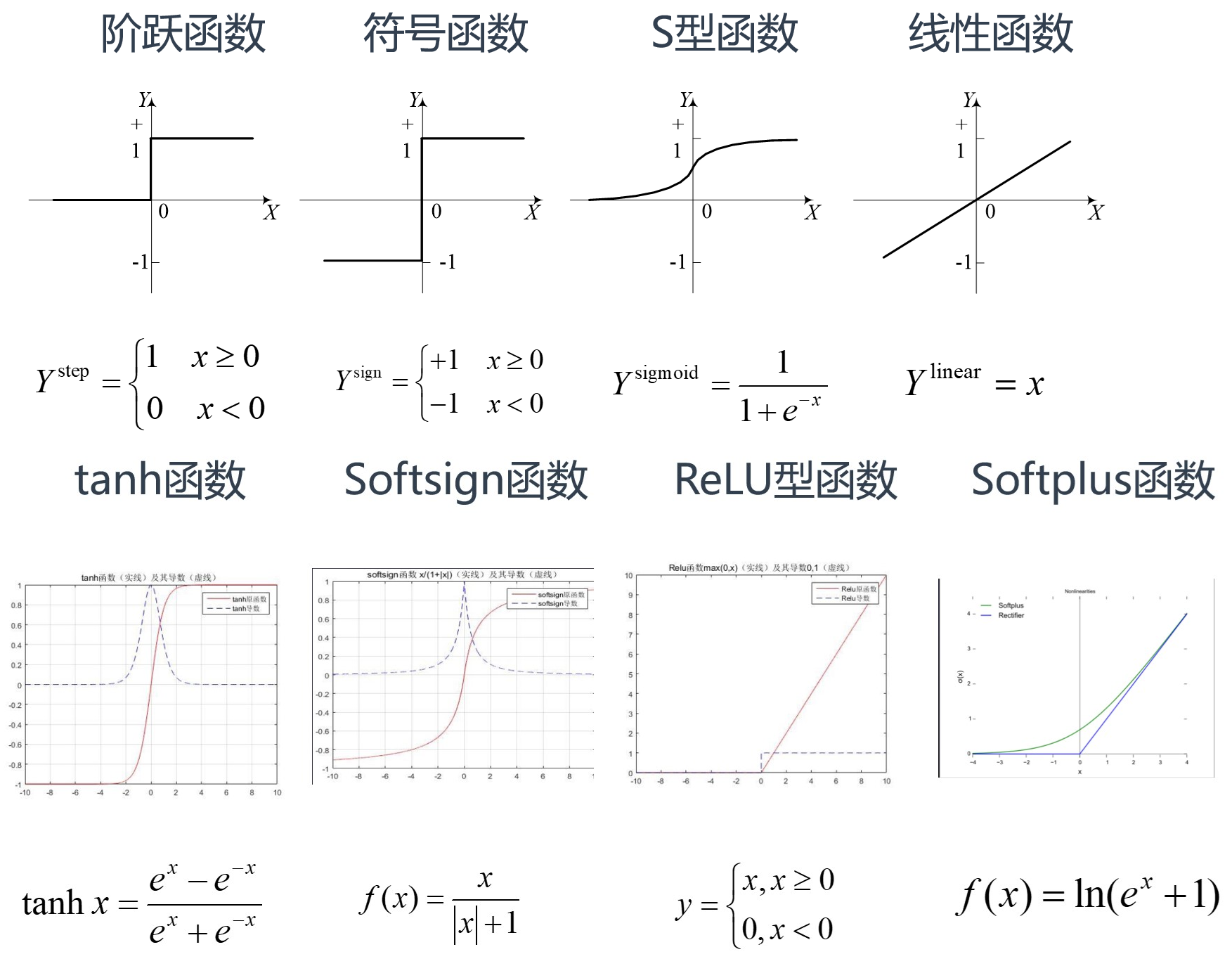
激活函数设计一般需要考虑的因素：

• 非线性
• 连续可微性
• 有界性
• 单调性
• 平滑性
• 原点附近近似 Identity

基本模型：

感知器

感知器基于 M-P 神经元模型。该模型由一个可调整权重的神经元(线性组合器)和一个硬限幅器组成。输入的加权和施加于硬限幅器，硬限幅器当其输入为正时输出为+1，输入为负时输出为-1（也可以是其他情况，具体由激活函数决定）。

一个基本感知器，用超平面将 n 维空间分为两个决策区域，超平面由线性分隔函数定义：

$$\sum_{i=1}^n x_iw_i-\theta =0$$

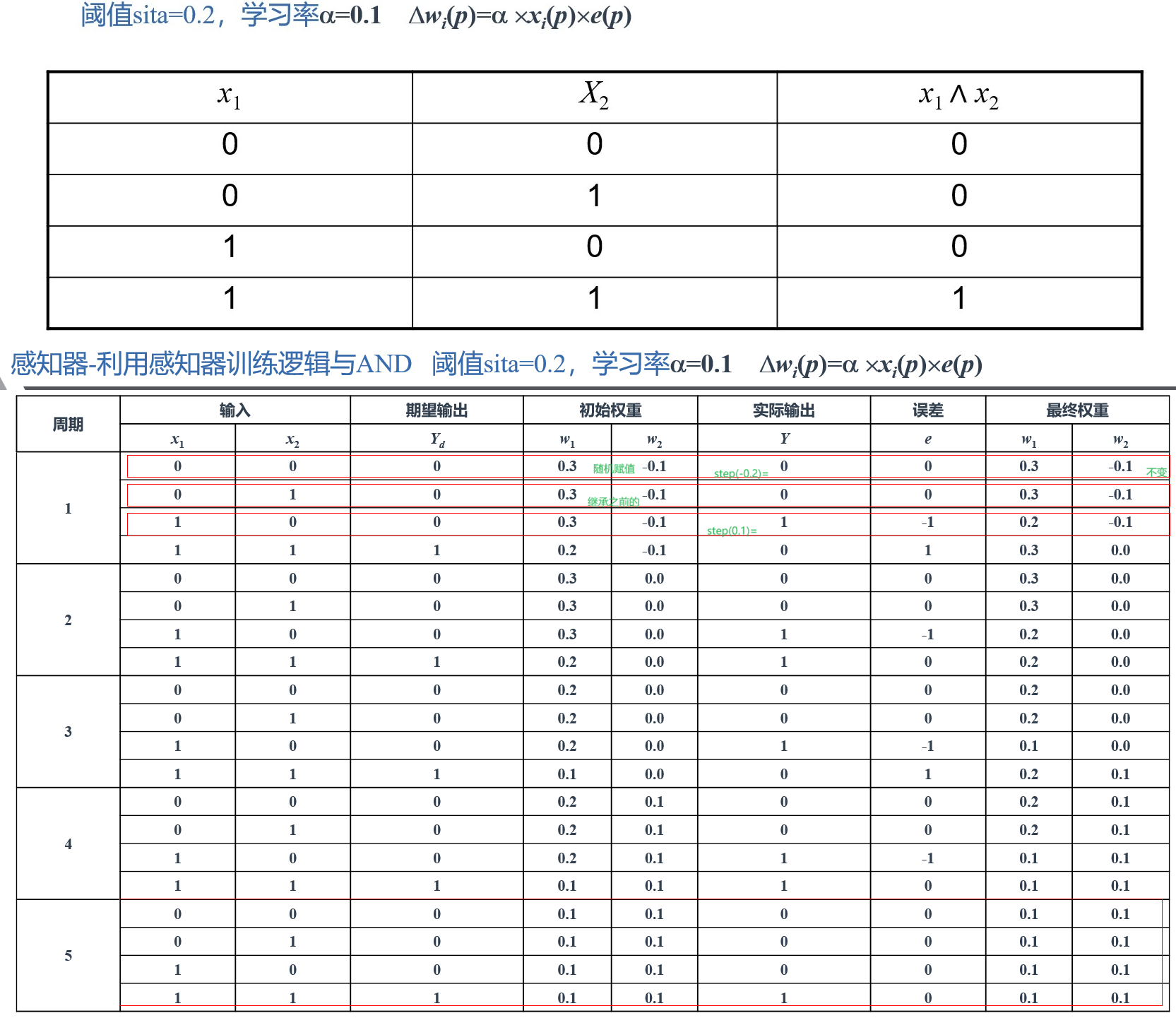
用于分类任务的感知器训练算法：

步骤1：初始化。设置权重w1, w2, … , wn和阈值 $\theta$ 的初值。初始权重可以随意赋值，取值范围通常为 [-0.5, 0.5] ，然后通过训练样本调整。
步骤2：激活。通过用输入x1(p), x2(p), … ,xn(p)以及期望输出 $Y_d(p)$ 来激活感知器。迭代 p 时的实际输出为：

$$Y(p) = \text{step} [\sum_{i=1}^n x_i(p) w_i(p)-\theta]$$

其中，n 为感知器输入的数量，step 为阶跃激活函数。
步骤3：权重训练。修改感知器的权重为：

$$w_i(p+1)= w_i(p)+ \Delta w_i(p)$$

其中， $\Delta w_i(p)=\alpha x_i(p)e(p)$ . e(p) 为误差。
步骤4：迭代。迭代 p 加 1，回到步骤 2，重复以上过程直至收敛。

例子：

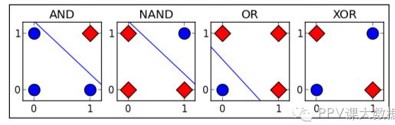
感知器仅能学习线性分割函数，单层感知器只能解决线性分类问题。XOR 问题中无法找到一条合适的线进行分类。

多层感知器可以解决非线性分类问题。

可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制，使其能处理更普遍的函数关系类型。

最简单的方法是将许多全连接层堆叠在一起。每一层都输出到上面的层，直到生成最后的输出。我们可以把前 L−1 层看作表示，把最后一层看作线性预测器。这种架构通常称为多层感知机（multilayer perceptron），通常缩写为 MLP。

梯度下降、损失函数

当训练样例线性不可分时，我们无法找到一个超平面，令感知器完美分类训练样例，但是我们可以近似的分类它们，而允许一些小小的分类错误。怎样让这个错误最小呢，首先要参数化描述这个错误，这就是损失函数（误差函数），它反映了感知器目标输出和实际输出之间的错误。最常用的误差函数为 L2 误差：

$$E(w) = \frac{1}{2} \sum_{d \in D} (t_d - o_d)^2$$

其中，d 为训练样例，D 为训练样例集，$t_d$ 为目标输出，$o_d$ 为实际输出。

梯度下降算法：

• 全局梯度下降算法
• 随机梯度下降算法
• Mini-Batch 梯度下降算法

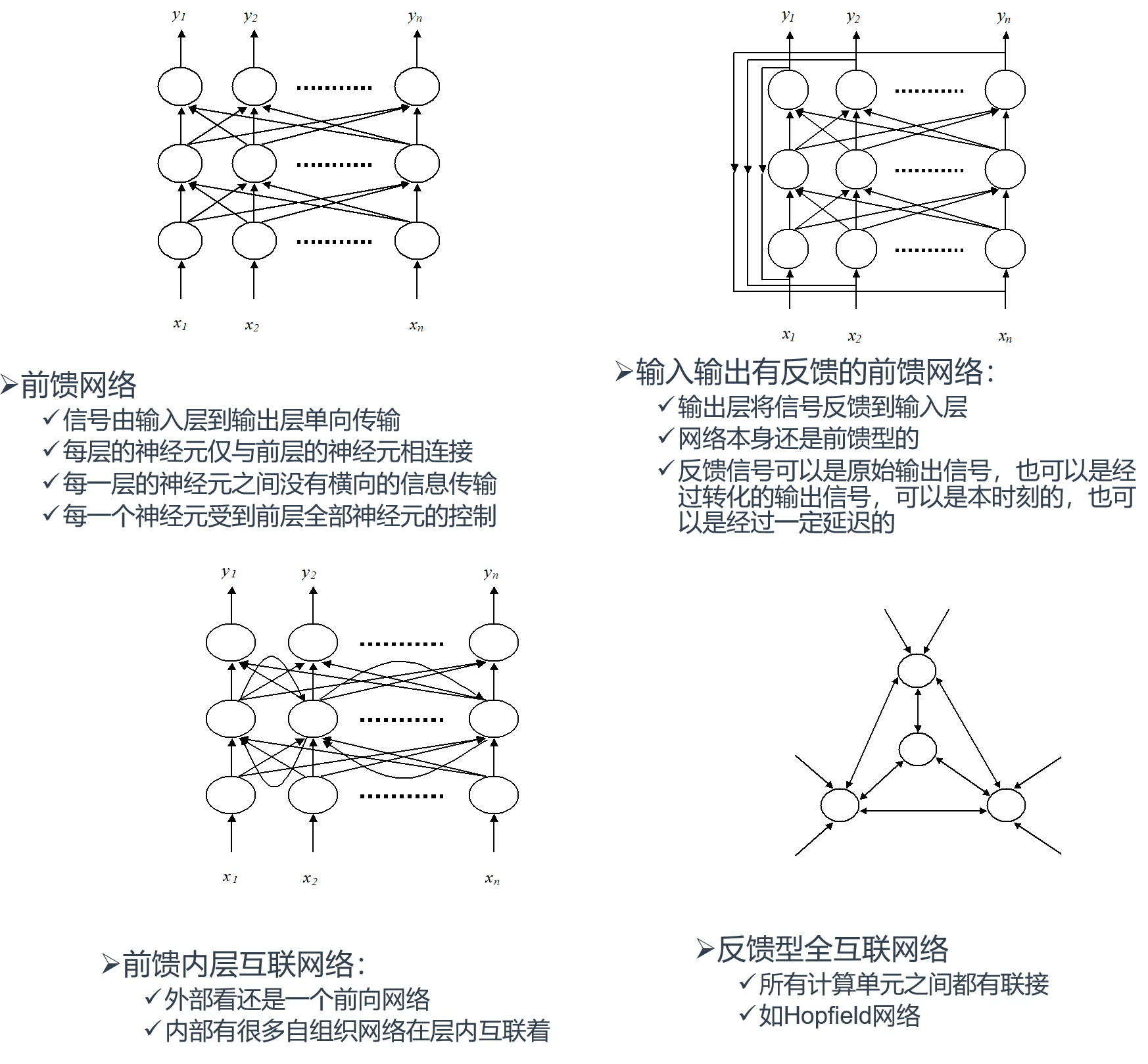
BP 网络

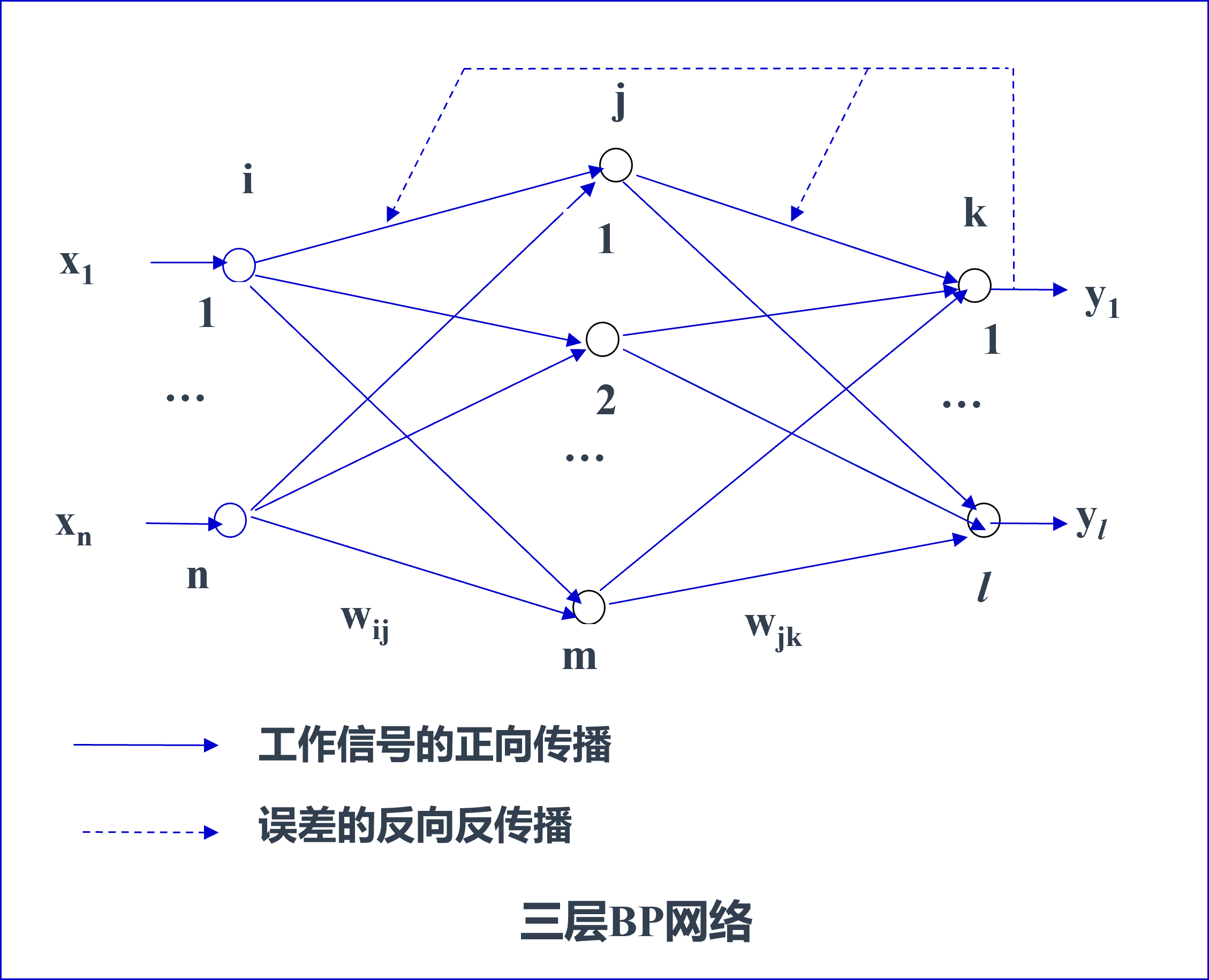
BP 网络学习的网络基础是具有多层前馈结构的 BP 网络。为讨论方便，采用如下所示的三层 BP 网络。

对上述三层 BP 网络，分别用 i,j,k 表示输入层、隐含层、输出层节点，且以下符号表示：

• $O_i$, $O_j$, $O_k$ 分别表示输入层节点 i、隐含层节点 j，输出层节点 k 的输出；
• $I_i$, $I_j$ ,$I_k$ 分别表示输入层节点 i、隐含层节点 j，输出层节点 k 的输入；
• $w_{ij}$, $w_{jk}$ 分别表示从输入层节点 i 到隐含层节点 j ，从隐含层节点 j 输出层节点 k 的输入节点 j 的连接权值；
• $θ_j$ 、$θ_k$ 分别表示隐含层节点 j、输出层节点 k 的阈值。

计算过程和之前大体相当。

BP 网络的激发函数通常采用连续可微的函数，例如 sigmoid 函数：

$$f(x) = \frac{1}{1+e^{-x}}$$

其一阶导数为：

$$f'(x) = f(x) [1-f(x)]$$

BP 网络学习过程是一个对给定训练模式，利用传播公式，沿着减小误差的方向不断调整网络联结权值和阈值的过程。

设样本集中的第 r 个样本，其输出层结点 k 的期望输出用 $d_{rk}$ 表示，实际输出用 $y_{rk}$ 表示。其中，$d_{rk}$ 由训练模式给出，且

$$y_{rk} = O_{rk}$$

如果仅针对单个输入样本，其实际输出与期望输出的误差为

$$E = \frac{1}{2} \sum_{k=1}^l (d_k - y_k)^2$$

上述误差定义是针对单个训练样本的误差计算公式，它适用于网络的顺序学习方式。若采用批处理学习方式，需要定义其总体误差。假设样本集中有 R 个样本，则对整个样本集的总体误差定义为：

$$E_R = \sum_{r=1}^R E_r = \frac{1}{2} \sum_{r=1}^R \sum_{k=1}^l (d_{rk} - y_{rk})^2$$

针对顺序学习方式，其联结权值的调整公式为

$$w_{jk}(t+1) = w_{jk}(t) + \Delta w_{jk}$$

式中，$w_{jk}(t)$ 和 $w_{jk}(t+1)$ 分别是第 t 次迭代和 t+1 次迭代时，从结点 j 到结点 k 的联结权值；$\Delta w_{jk}$ 是联结权值的变化量。

在开始推导之前，补充一点知识：

其实下面的推导只会用到这个 pdf 最开始的概念。多数情况下可以非常粗糙地理解——只要记住某些符号其实代表了一个向量，而每个向量都有很多元素，但是都可以用同一种方法计算，因而将它们记成了向量。

为了使联结权值能沿着 E 的梯度下降的方向逐渐改善，网络逐渐收敛，权值变化量 $\Delta w_{jk}$ 的计算公式如下：

$$\Delta w_{jk} = - \eta \frac{\partial E}{\partial w_{jk}}$$

式中，$\eta$ 为增益因子，取 [0, 1] 区间的一个正数，其取值与算法的收敛速度有关。

$$\frac{\partial E}{\partial w_{jk}} = \frac{\partial E}{\partial I_k} \frac{\partial I_k}{\partial w_{jk}}$$

注：E 是一个复合函数，这里用了链式法则。这样拆分是有实际意义的，比较显然。

$$\frac{\partial I_k}{\partial w_{jk}} = \frac{\partial}{\partial w_{jk}} \sum_{j=1}^m w_{jk} O_{j} = O_j$$

令局部梯度

$$\delta _k = - \frac{\partial E}{\partial I_k}$$

注意，这里 $\delta _k$ 代表了 $l$ 个变量，它们具有类似的形式。

那么有

$$\Delta w_{jk} = -\eta \frac{\partial E}{\partial I_k} \frac{\partial I_k}{\partial w_{jk}} = \eta \delta _k O_j$$

对于输出层上的结点，则有 $O_k=y_k$ ，因此（这里 $y_k$ 也是向量）

$$\delta _k = - \frac{\partial E}{\partial I_k} = - \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial I_k}$$

得到

$$\begin{aligned} \frac{\partial E}{\partial y_k} &= \frac{\partial}{\partial y_k} ( \frac{1}{2} \sum_{i=1}^l (d_i - y_i)^2 ) \\ &= \frac{1}{2} \cdot 2 (d_k - y_k) \cdot (-1) \\ &= -(d_k - y_k) \end{aligned}$$

又因为

$$\frac{\partial y_k}{\partial I_k} = f'(I_k - \theta)$$

所以

$$\delta _k = (d_k - y_k) f'(I_k - \theta)$$

又因为 $f(I_k - \theta) = y_k$ ，再由 sigmoid 函数的导数的公式，有

$$\delta _k = (d_k - y_k) y_k (1-y_k)$$

代入之前的结果：

$$\Delta w_{jk} = \eta (d_k - y_k) (1 - y_k) y_k O_j$$

那么，对输出层有：

$$\begin{aligned} w_{jk}(t+1) &= w_{jk}(t) + \Delta w_{jk} \\ &= w_{jk}(t) + \eta (d_k - y_k) (1-y_k) y_k O_j \\ \end{aligned}$$

现在，我们想要类似地计算 $\Delta w_{ij}$ 。

对于不是输出层的结点。它表示联结权值是作用于隐含层上的结点，我们可以类似地定义 $\delta _j$ ：

$$\delta _j = - \frac{\partial E}{\partial I_j} = - \frac{\partial E}{\partial O_j} \frac{\partial O_j}{\partial I_j}$$

容易得到：

$$\delta _j = - \frac{\partial E}{\partial O_j} f'(I_j - \theta _j)$$

为了便于理解，下面的 $O_j$ 可以理解为隐藏层中的随意一个节点的输出值（实际上它是向量）：

$$\begin{aligned} -\frac{\partial E}{\partial O_j} &= - \frac{\partial E}{\partial I_k} \frac{\partial I_k}{\partial O_j} \\ &= (-\frac{\partial E}{\partial I_k}) \cdot \frac{\partial}{\partial O_j} \sum_{j=1}^m w_{jk} O_j \\ &= (- \frac{\partial E}{\partial I_k}) w_{jk} \\ \end{aligned}$$

上面式子最后结果中的 $w_{jk}$ 是指该 $O_j$ 对应的权值。

这个结果非常的 amazing 啊，注意到

$$\delta _k = - \frac{\partial E}{\partial I_k}$$

于是有：

$$-\frac{\partial E}{\partial O_j} = \delta _k w_{jk}$$

于是

$$\delta _j = \delta _k w_{jk} f'(I_j - \theta _j)$$

这说明，低层结点的 $\delta$ 值是通过上一层结点的 $\delta$ 值来计算的。这样，我们就可以先计算出输出层上的 $\delta$ 值，然后在较低层上计算。

$$\delta _j = \delta _k w_{jk} f(I_j - \theta _j) [1 - f(I_j - \theta _j)]$$

于是

$$\begin{aligned} \Delta w_{ij} &= \eta \delta _k w_{jk} f(I_j - \theta _j) [1 - f(I_j - \theta _j)] O_i \\ &= \eta \delta _k w_{jk} O_j (1 - O_j) x_i \end{aligned}$$

那么，对隐含层有：

$$\begin{aligned} w_{ij}(t+1) &= w_{ij}(t) + \Delta w_{ij} \\ &= \text{代入即可} \cdots \\ \end{aligned}$$

BP 网络的算法流程：

拓展内容

目录
卷积神经网络(CNN) 2
RNN 6
LSTM结构 9
注意力机制 11
正则化与优化器 18