Perlin Noise
柏林噪声算法常用于程序生成随机内容,在游戏、电影等领域应用广泛。
本文的目标是使用 Python 生成如下的图像,由这个图像出发可以实现很多效果[1]。
虽然柏林噪声算法有一个改进版本[2],但本文仍是基于旧原理的实现。
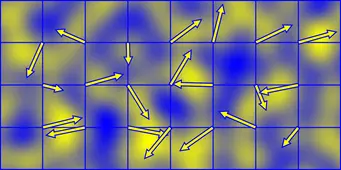
很多时候,我们并不是想要这样的随机:
我们需要更平滑的随机,就像本文第一张图片那样。
39-1.jpg(第一张图片)是一张灰度图,可以将其每个像素的灰度值映射为数值,用二维坐标索引,就得到一个三维的曲面(如果你愿意忽略它是离散的的话)。显然 39-1.jpg 就像是杂乱的水面,而 39-2.png 就是钉床了(虽然由于钉子非常密集躺上去应该还不至于当场去世)。
Perlin 的做法是:
在网格上生成图片,每个小格子称为“晶格”。首先,在格点上生成一个随机的梯度向量。对于晶格内的点,作由四个晶格格点到自身的向量,这些向量与对应的四个梯度向量作点积,得到格点上的四个数值,那么对于此晶格内的点,噪声值就是这四个数值的双线性插值[3]。此外,你可能需要一个 $fade$ 函数使图像更平滑。
But wait … , why it even works ?
一个可能的解释:
对此我也不是很清楚。虽然这大致和梯度的几何意义有关(想象一下那个三维曲面),但是还是有一些细节不能理解。等以后搞明白了再说。
OK,原理介绍完了,缝一个简陋的代码:
1 | import numpy as np |
再放一张输出结果:
顺带一提,这种噪音图会引起博主的轻微不适,原因不明。
我们假设,图片一共被划分为 $x\cdot y$ 个晶格,横向 $x$ 个,纵向 $y$ 个。每个晶格是 $l\cdot l$ 像素的正方形。
向量场格点从 $0$ 开始编号,横:$0,1,2,\cdots ,x$ ;纵:$0,1,2,\cdots ,y$ .
晶格从 $0$ 开始编号,$(0,0),(0,1),\cdots ,(0,x-1);\cdots$
对于每个晶格,处理过程是类似的:
1 | for i in range(x): |
每个晶格里面,需要填充每个像素的噪声值。如何计算这个噪声值,上文已经提过。
其中,single_point_noise函数是在连续意义下的单位正方形中计算点的噪声值,而在生成图片时,却是离散的像素点。这里我直接简单粗暴地使用像素点的几何中心坐标,传值到single_point_noise函数中。另外,由于是单位正方形,所以值要除以 $l$ .
在此基础上,有一个简单的拓展:如果在时间维度上插值,就可以制作出三维的情形,或是动态变化的二维柏林噪声——这两者是一回事。
1 | import numpy as np |
将得到的图片转为 GIF(博客中的 PythonNote 有提),最终输出结果如下:
这个动图看起来动静似乎不明显,这是因为设置了t=1 ,过大的话计算量太大。将 t 再稍微放大点,gif 的时间间隔缩短点,效果就会好很多。
在拓展维度时,代码的编写很大程度上是出于对某种统一形式的信仰——这代码就该这么写,而不需要考察其细节。在编写代码的时候,我甚至没有查找三线性插值是如何进行的。
最后的 tip : 上面代码的输出文件名可能不太好,因为在合成 gif 时,顺序可能是按严格的字典序排的。我是最后手动修改了文件名,反正也不多,就没有改代码了,因为很讨厌处理字符串。
记录一下最近看的感觉不错的电影,因为实在没必要开个新文章写这些:壳中少女、末代皇帝。另外在看我推,目前看着还行。
[1] The Absurd Usefulness of Noise in Game Development
[2] Ken Perlin’s SIGGRAPH 2002 paper: Improving Noise (已备份)
[3] 维基百科 双线性插值 (已备份)