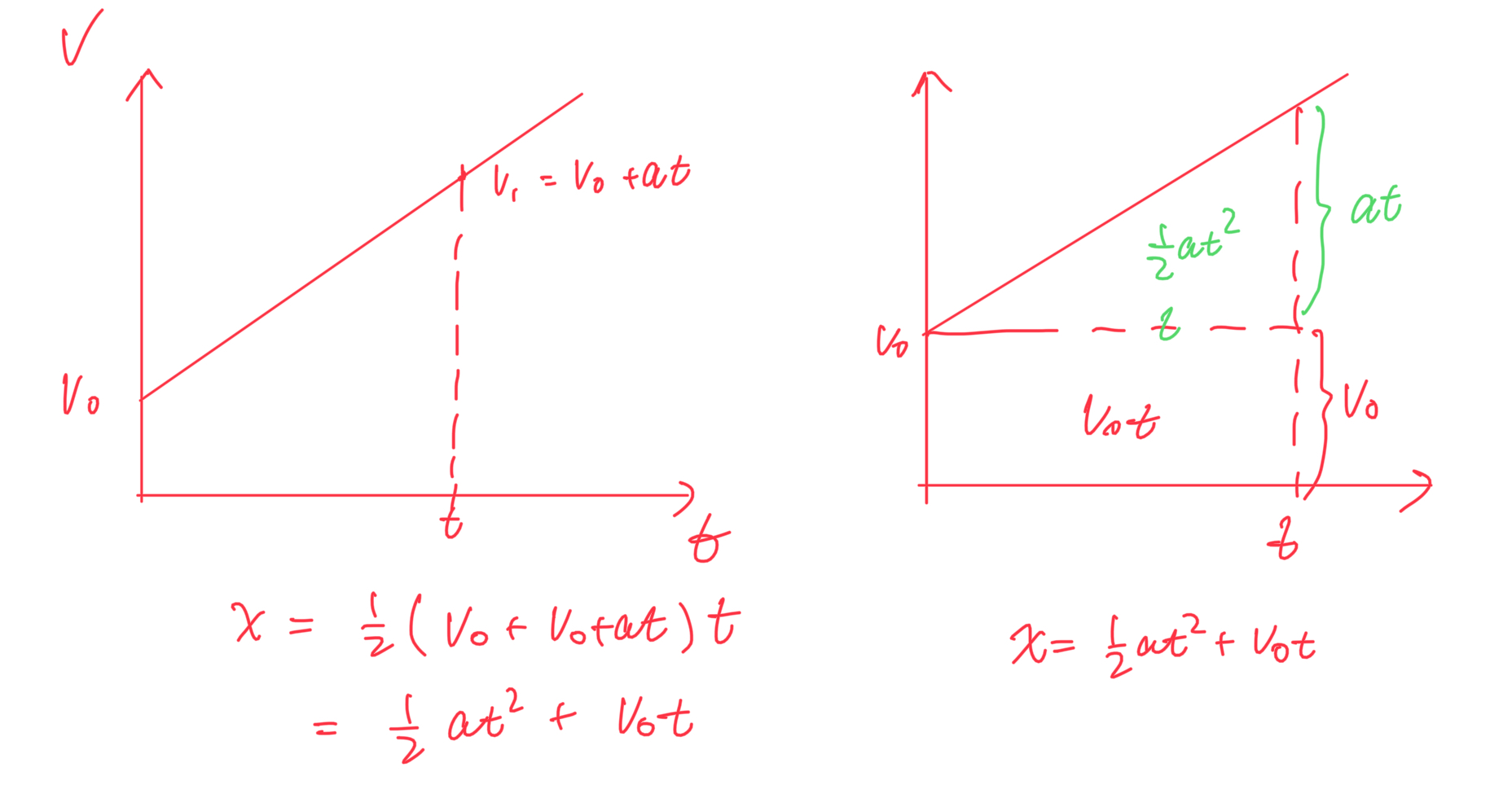高中物理讲义

非常惭愧地又带了一个高中生。

在之前的基础上重新整理了讲义，并添加了新内容。

实际上教学中会有更多例题，但这篇文章主要是给我自己串知识点的，简单的题目我应该可以推出来，因此不放了。

持续更新中…

运动的描述

知识点梳理

质点：理想模型，忽略大小形状，具有质量。

• 具体问题具体分析

例题：

参考系：描述物体运动时选定的参考。

位移：矢量，由起点指向终点，大小和方向。

速度：位移与发生该位移的时间的比。 $v=\Delta x/\Delta t$

• $1m/s=3.6km/h$
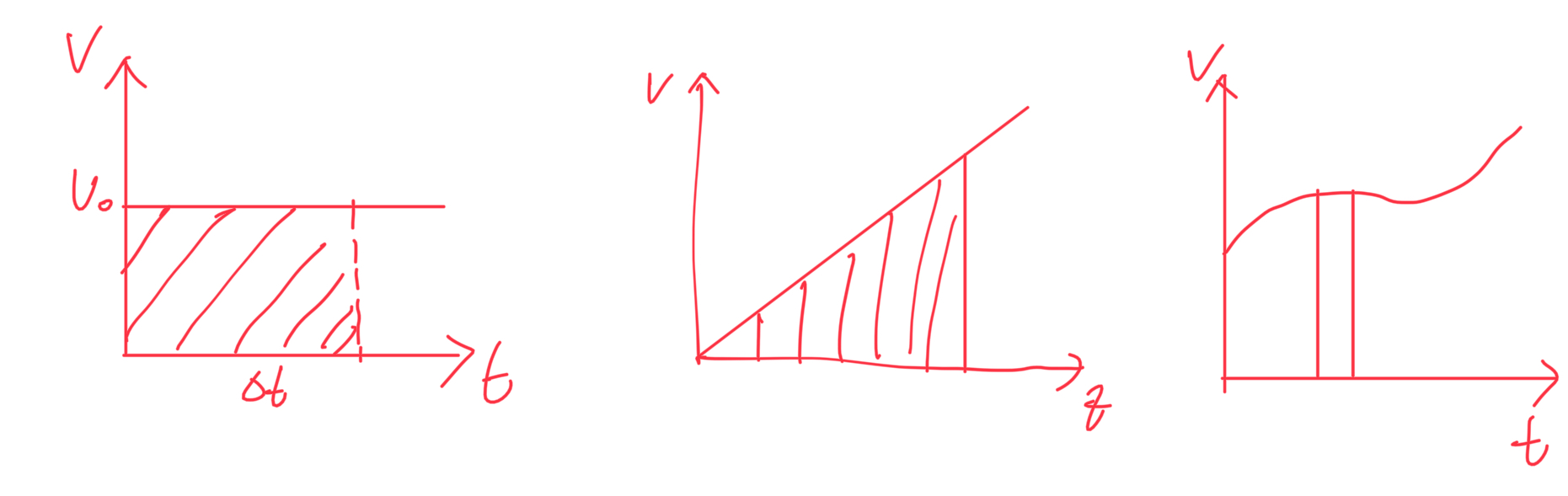
• $v-t$图像，与$x-t$图像的关系，几何意义

v-t 图像 直线/曲线 下方面积就是位移。

例题：

平均速度：$\overline{v}=\dfrac{\Delta x}{\Delta t}$ $\quad$ 瞬时速度：$v=\dfrac{\Delta x}{\Delta t}(\Delta t \to 0)$

例题：

加速度：速度的变化率。 $a=\Delta v/\Delta t$

• 加速度具有方向，在未声明正方向的题目中需自行声明。
• $v-t$图像中的加速度。

速度与加速度的关系：

练习

匀变速直线运动

知识点梳理

定义

匀变速直线运动：加速度不变的直线运动。

在辨析题中注意区分，例如圆周运动、平抛运动可以作为很多反例。

公式

通过 $v-t$ 图像理解 $x=\dfrac{1}{2}at^2+v_0t$ 的导出：

并通过类似方法理解匀变速运动中中点时刻速度等于平均速度（自行完成）。

联立 $x=\dfrac{1}{2}at^2+v_0t$ 与 $v=at+v_0$ 得到：

$v^2-v_0^2=2ax$

重要推论

$$\Delta x=aT^2$$

含义：匀变速直线运动中，任意相等的连续时间间隔 $T$ 内位移之差为定值 $aT^2$

拓展（方便理解）：对于一个符合二次函数的数列，例如：

$$1,4,9,16,25,... \quad (1)$$

逐项作差：

$$3,5,7,9,\quad ...(2)$$

对 $(2)$ 继续作差：

$$2,2,2,\quad ...(3)$$

将得到定值。

这个规律对任一以二次函数为数列通项公式的数列都成立。

其中数列 (1) 可理解为位移，数列 (2) 理解为速度。而数列 (3) 中的数与二次函数的二次项系数有关，在匀变速直线运动中与加速度有关。

推论 $\Delta x=aT^2$ 实质上与此类似， 在 $x-t$ 图像（$x=\dfrac{1}{2}at^2+v_0t$ 为二次函数）上等距取点，算出函数值作差（第一次作差）得到等间隔内的位移,将此位移继续作差（第二次作差）得到定值。

拓展（小车实验的基础）：第 $m$ 个时间 $T$ 内与第 $n$ 个时间 $T$ 内的位移差：

$$\Delta x=x_m-x_n=(m-n)aT^2$$

重要的比例式

初速度为 0 的匀加速直线运动中几个重要的比例式：

• 时间等分
• 位移等分
  • 前 nx
  • 第 n 个 x

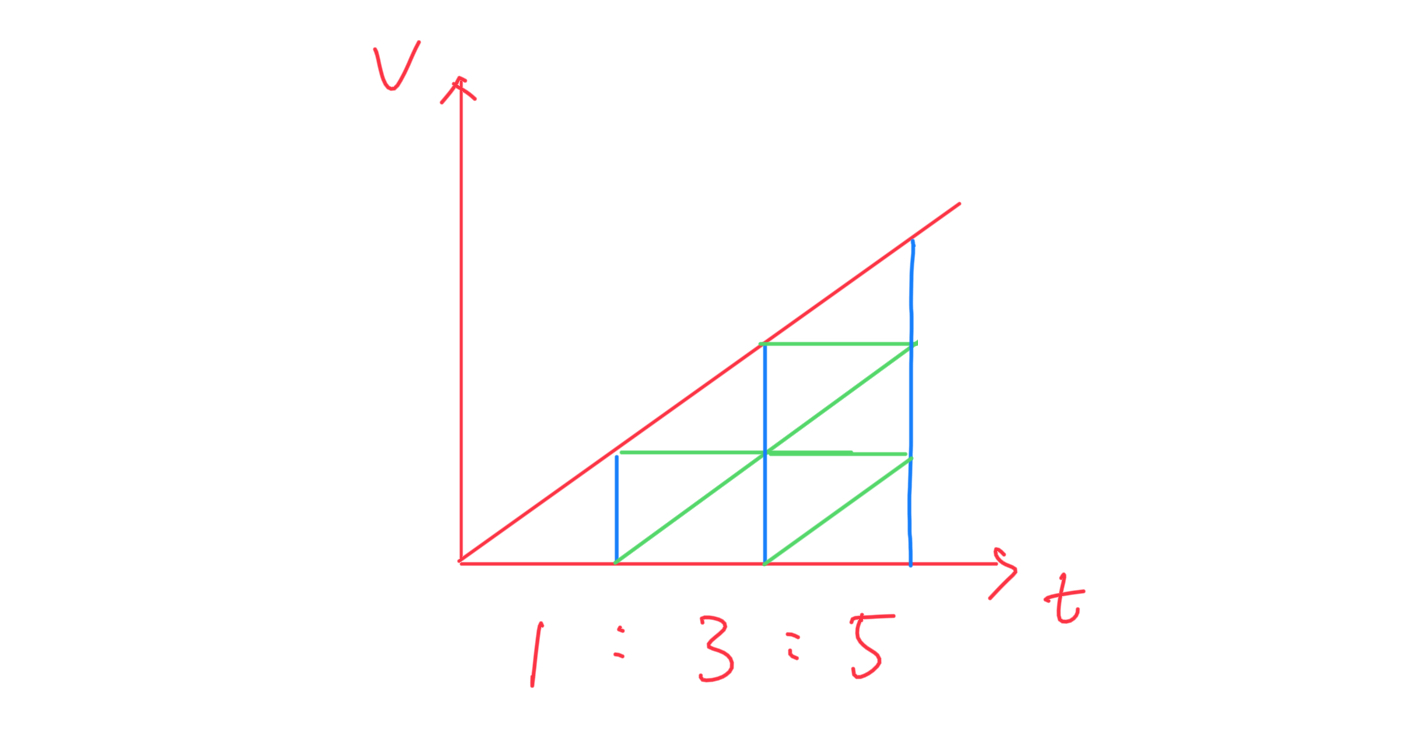
时间等分：第一个 T 内、第二个 T 内、第三个 T 内、… 的位移之比为 1 : 3 : 5 : …

位移等分（前 nx）：通过前$x$，前$2x$，$…$,前$nx$位移时的速度之比为：

$$v_1:v_2:v_3:...:v_n=1:\sqrt 2:\sqrt 3:...:\sqrt n$$

推导方法，由 $v^2-v_0^2=2ax$ 导出：

$$v^2-v^2_0=2ax$$ $$x=\frac{1}{2a}(v^2-v_0^2)=\frac{v^2}{2a}$$ $$\frac{2x}{x}=2=\frac{v_2^2}{v_1^2}$$ $$\frac{v_2}{v_1}=\sqrt{2}$$ $$\frac{v_3}{v_1}=\sqrt{3}$$ $$\cdots$$

位移等分（第 n 个 x）：通过第一个 $x$，第二个 $x$，$…$，第 $n$ 个 $x$ 所用时间之比：

$$t_1:t_2:t_3:...:t_n=1:(\sqrt 2-1):(\sqrt 3-\sqrt 2):...:(\sqrt n-\sqrt{n-1})$$

推导方法：因为初速度为零，速度正比于时间。至此，由 位移等分（前 nx） 的公式不难得到。

自由落体、竖直上抛

自由落体运动：匀变速直线运动的一种特例，$a=g$，$v_0=0$ .

$$v=gt,x=\dfrac{1}{2}gt^2$$

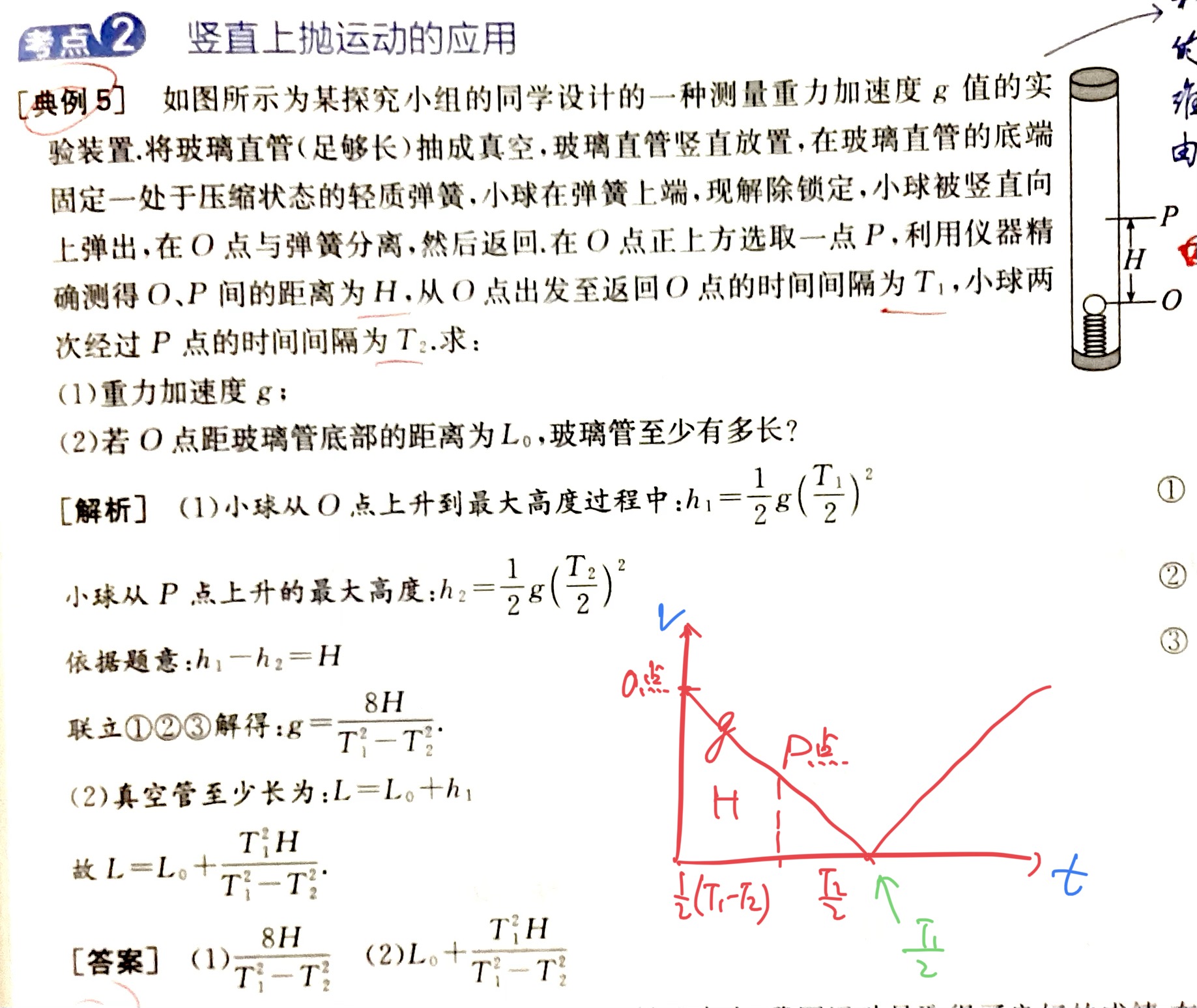
竖直上抛运动：仍然是匀变速直线运动的一种

实验 小车测加速度

实验 - 小车速度随时间的变化规律 的注意点:

• 交流电频率 $50Hz$ ，打点计时器打出的两点时间间隔为$0.02s$
• 小车释放位置：靠近打点计时器
• 先接通电源打点，后释放小车
• 改变钩码数量，重复实验
• 实验方案创新，频闪照相，等效替代等，通过 $v-t$ 图像理解剪下纸带的长度

一种常见的数据处理方法：

$$a=\frac{\Delta x}{(m-n)T^2}$$ $$a=\frac{x_4-x_1}{3T^2}=\frac{x_5-x_2}{3T^2}=\frac{x_6-x_3}{3T^2}$$ $$a=\frac{x_6+x_5+x_4-(x_3+x_2+x_1)}{9T^2}$$

练习

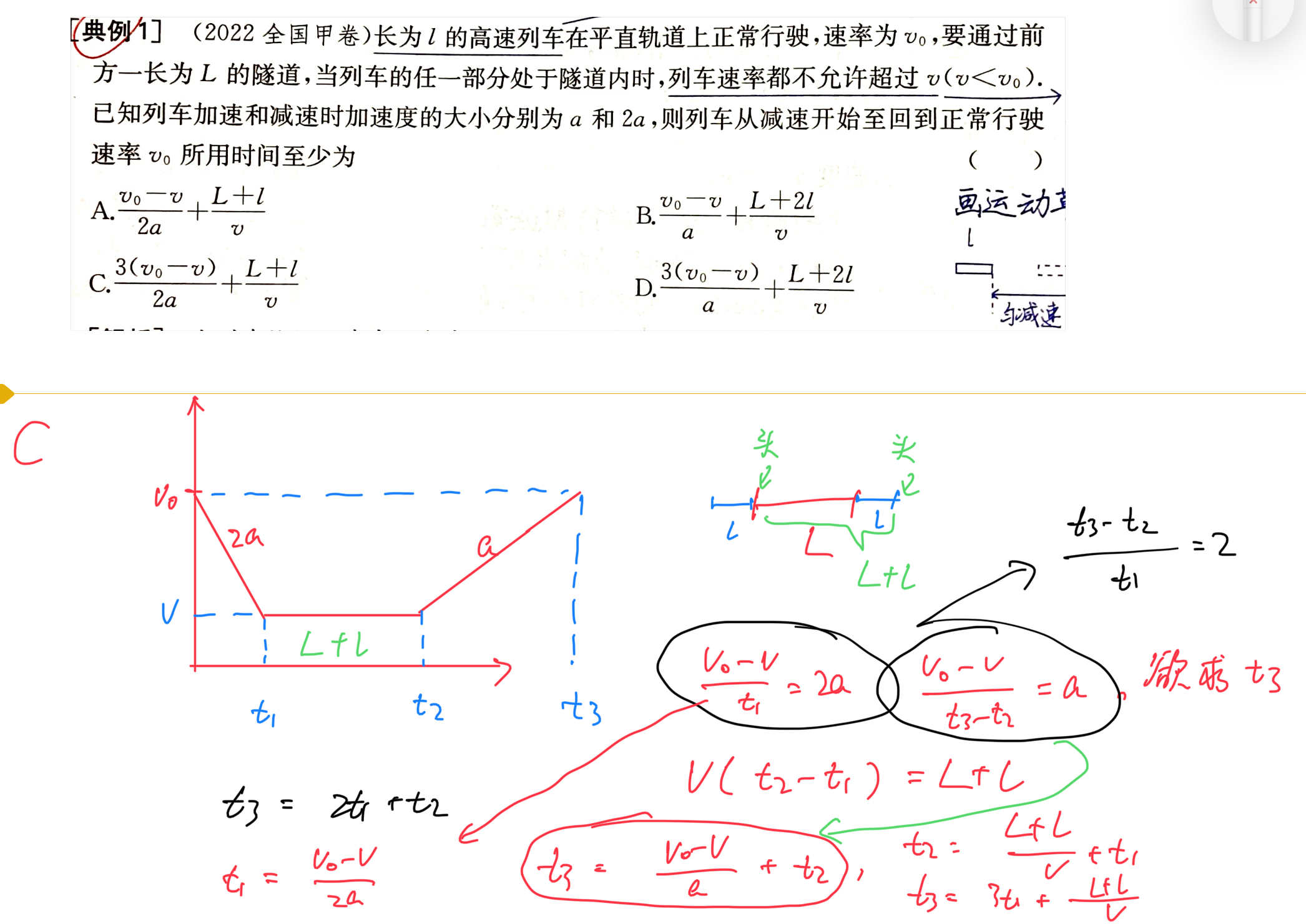
画图分析，列方程，解方程：

活用 v-t 图像：

力

重力 弹力 摩檫力

重力

定义：由于地球的吸引而使物体受到的力。

$$G=mg$$

注意：在地球表面附近可近似认为重力等于万有引力。 严格来说，只有在两极和赤道处，重力的方向才指向地心。其余位置，万有引力会分解为两个力：使物体随着地球自转的向心力 $F_{向}$ 和 $mg$ .

方向：竖直向下。 注意：竖直向下是和水平面垂直，不一定指向地心。

重心：因为物体的各部分都受到重力作用，在研究问题是可认为重力作用集中于物体的一点，即重心。质量分布均匀、形状规则的物体的重心在其几何中心上。

弹力

定义：形变的物体有恢复原状的趋势，对与之接触的物体产生力的作用，这种力叫做弹力。

产生条件：物体相互接触且发生弹性形变。

方向：与作用在物体上使之发生形变的外力方向相反。

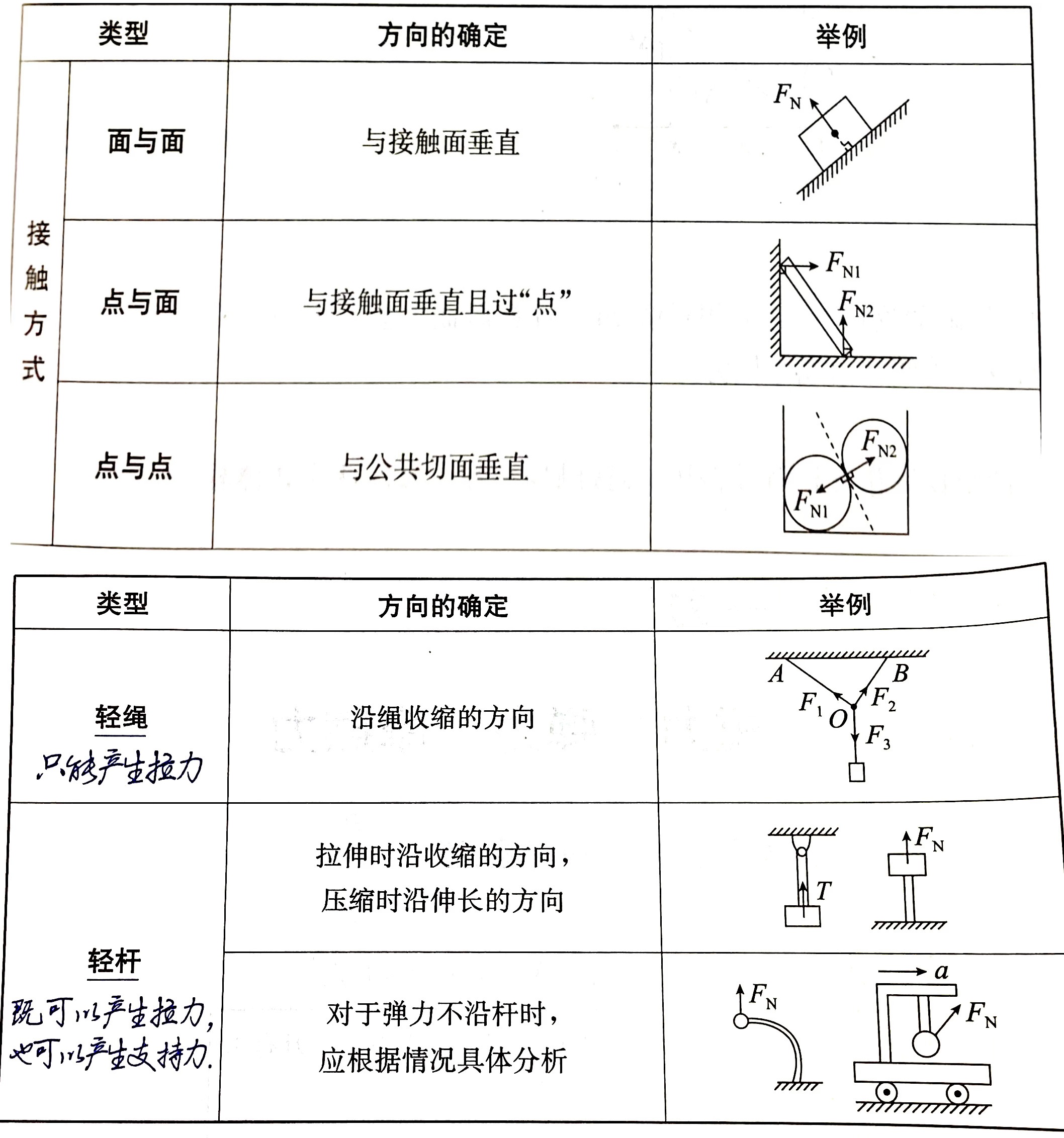
常见的弹力及其方向：

重要：接触面、绳、杆上的弹力可以突变。

胡克定律

内容：在弹性限度内（弹簧发生弹性形变），弹力 $F$ 的大小和弹簧长度的变化量 $x$ 成正比。

$$F=kx$$

其中 $k$ 称为劲度系数。

滑动摩檫力

定义：两个相互接触的物体，当它们相对滑动时，接触面上会产生阻碍这种相对运动的力，即滑动摩擦力。

产生的条件：

1. 接触面粗糙
2. 两个物体互相接触并挤压（即接触处有弹力）
3. 两个物体相对运动

方向：沿着接触面，与相对运动的方向相反。

大小：

$$F_f=\mu F_{压}$$

其中，$\mu$ 是动摩擦因数，与两个物体的材料和接触面的粗糙程度有关，与接触面的面积和运动速度无关。

静摩檫力

定义：相互接触的两个物体只有相对运动的趋势（并没有发生相对运动）时的摩檫力。

产生条件：

1. 接触面粗糙
2. 接触处有弹力
3. 两物体间有相对运动的趋势

大小（介于 0 和最大静摩擦力之间）：

$$0<F\le F_{max}$$

一点可有可无的细节补充：

1. 最大静摩擦力的大小和正压力近似成正比。
2. $F_{max}$ 略大于滑动摩檫力。在解题中，如无特别说明，可认为两者相等。

练习

在两个正交（互相垂直）的方向上分解力，列出等式，联立方程：

考虑如下的模型：

斜坡固定，物体静止在斜坡上，斜坡与物体之间有摩擦，动摩擦因数为 $\mu$, 斜坡的倾角为 $\theta$.

对物体受力分析：物体受重力、摩檫力、斜面对物体的弹力。

将重力分解为沿着斜坡向下的力和垂直指向斜坡的力，建立方程：

$$mg\cos \theta =F_n$$ $$f=mg\sin \theta =\mu F_n=\mu mg\cos \theta$$ $$\sin \theta = \mu \cos \theta$$ $$\mu = \tan \theta$$

即，在这种情况下，物体想要保持静止，斜面的动摩擦因数至少为 $\tan \theta$ ，若小于这个值，物体会因为重力沿着斜面向下的力大于摩檫阻力而向下滑落。

力的合成与分解

知识点梳理

合力：一个力可以等效替代某几个力的共同作用。

分力：合力所等效替代的那几个力。

力的合成遵循 平行四边形法则 / 三角形法则。

两个共点力的合力范围：

$$|F_1-F_2| \le F \le F_1 + F_2$$

三个共点力的合力大小范围：（可以由两个点的情形推广而来）…

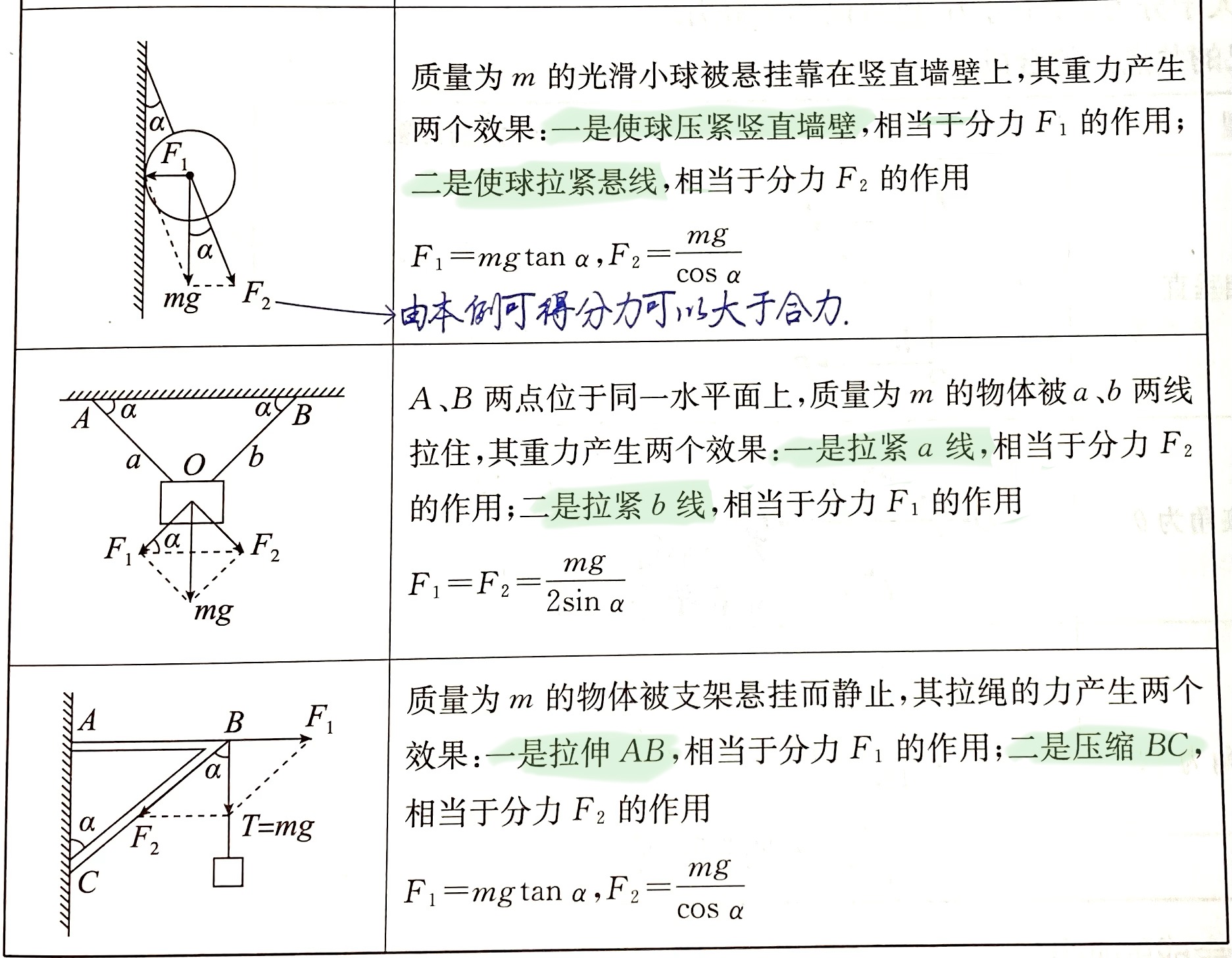
一些力的分解案例：

力的正交分解：将力分解到两个互相垂直的方向上。

专题 共点力平衡

受力分析的方法：整体法（不考虑系统内部的相互作用）、隔离法。