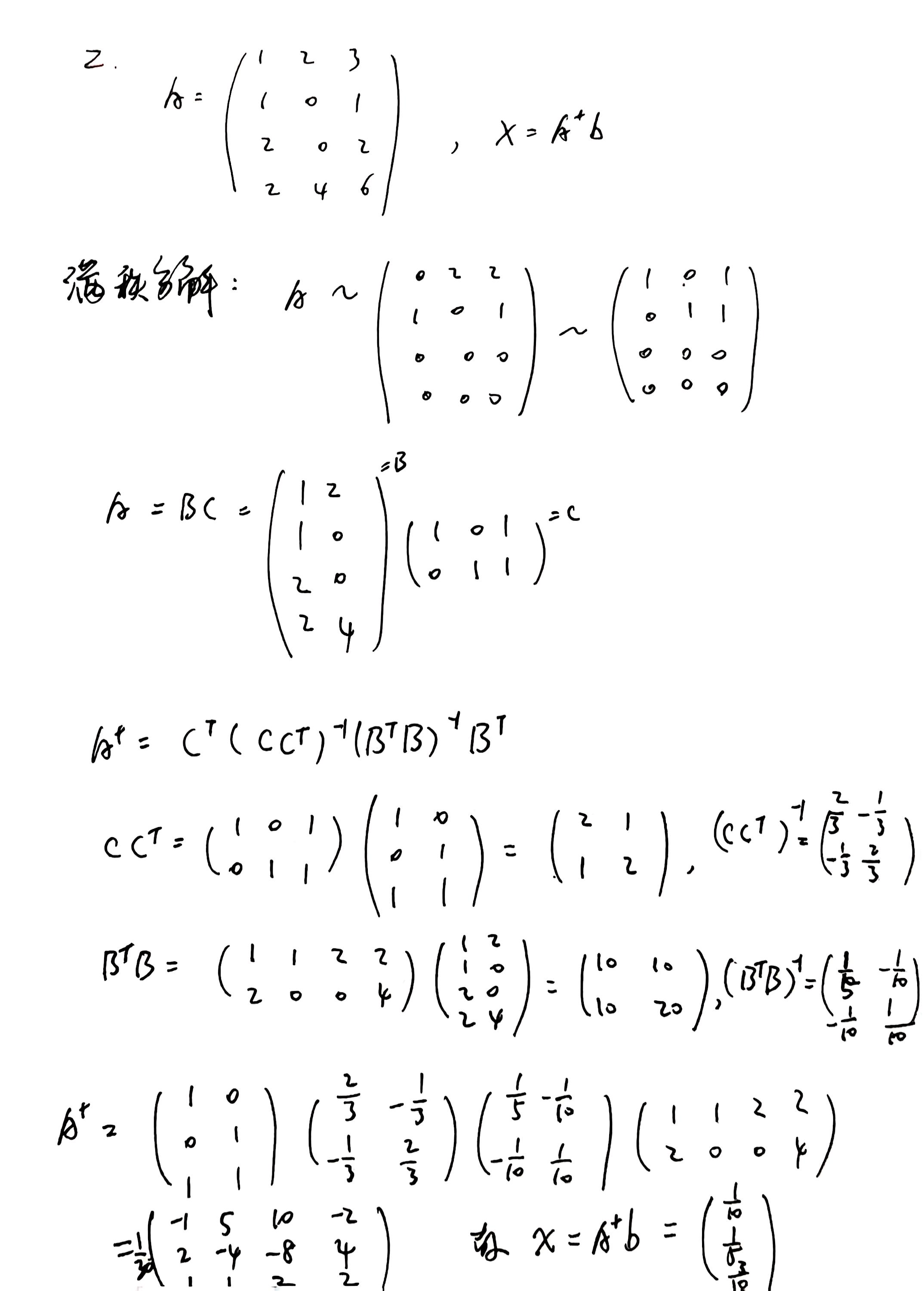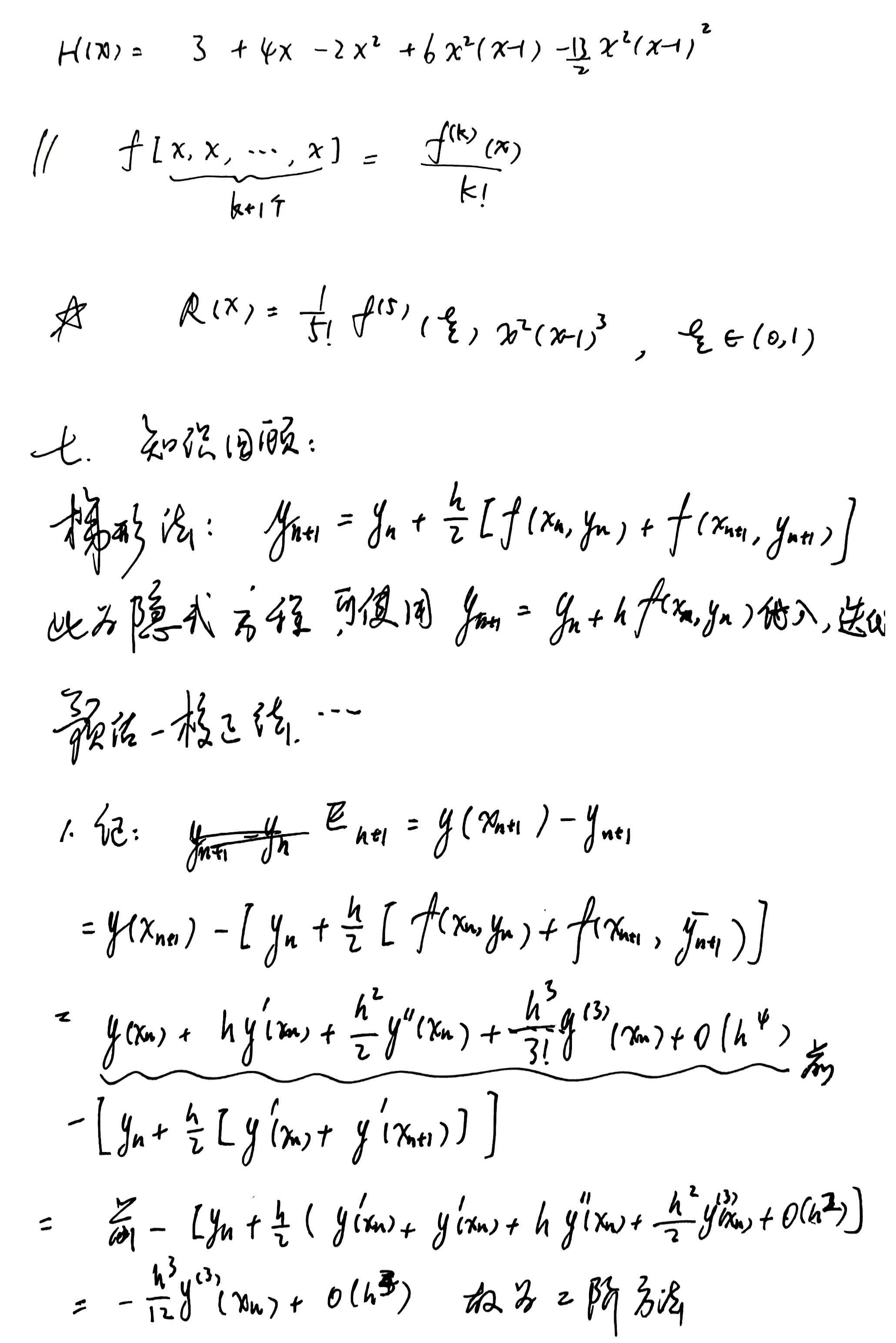矩阵论

一些内容补充可以参考之前的线性代数笔记。

矩阵论（上）：

目录
矩阵及其基本运算 4
矩阵的特征值与特征向量 5
特征值估计（圆盘定理） 7
LU 分解（Doolittle 分解，Crout 分解…） 12
QR 分解 26
满秩分解 27
奇异值分解 31
线性空间的基、维数与坐标 35
过渡矩阵 40
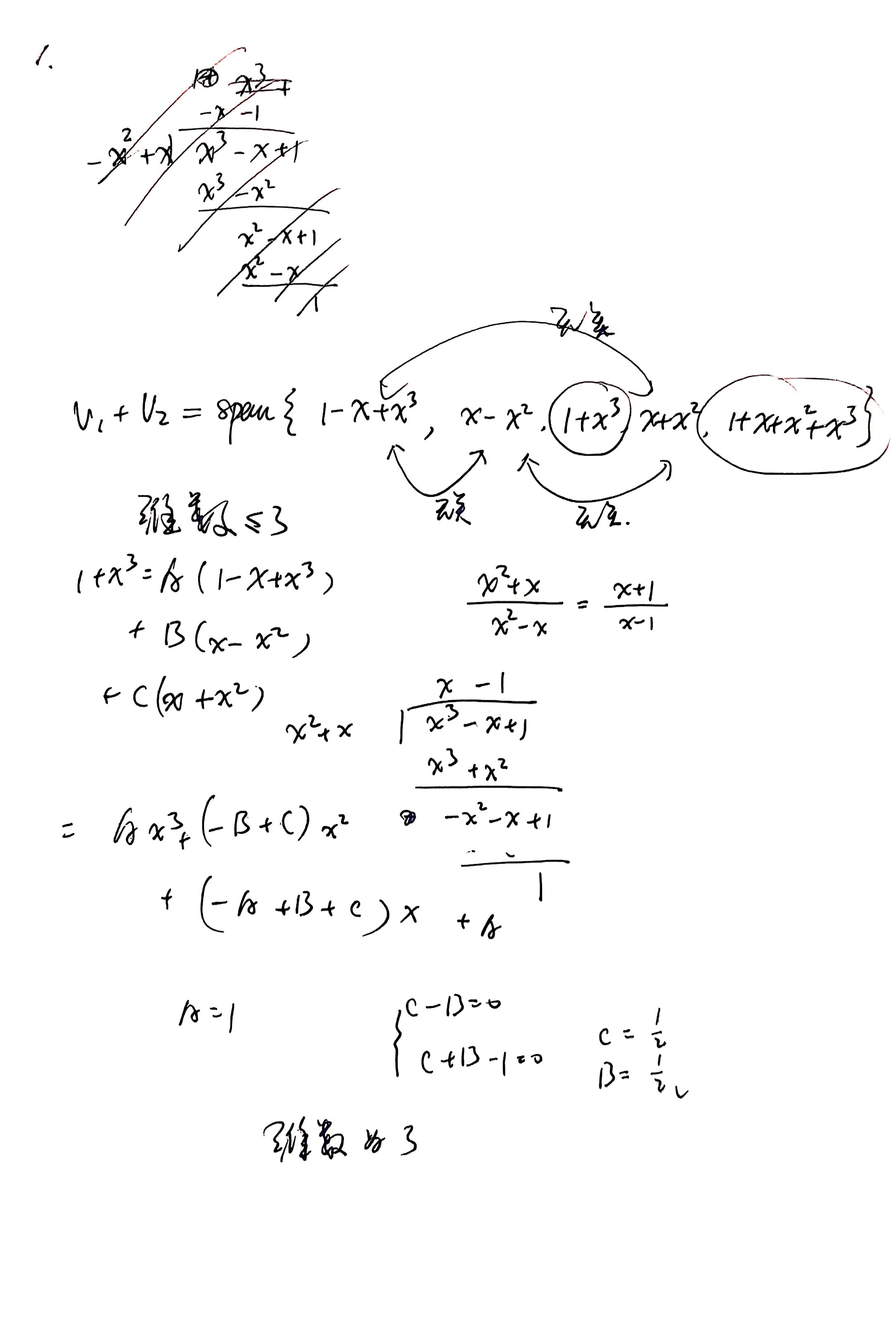
子空间交与和（和空间、直和、补空间） 47
广义逆 58
赋范线性空间 77
柯西不等式 83
方阵空间上的范数 85
向量范数的诱导范数 91
赋范线性空间中的距离 97
对角占优 100
内积空间 102
内积空间的度量矩阵 109
正交多项式 117

矩阵论（下）：

目录
线性变换及其运算 1
不变子空间 13
表示矩阵 14
λ 矩阵 28
Smith 标准型、不变因子 31
初等因子 33
k 阶行列式因子 35
Jordan 块 46
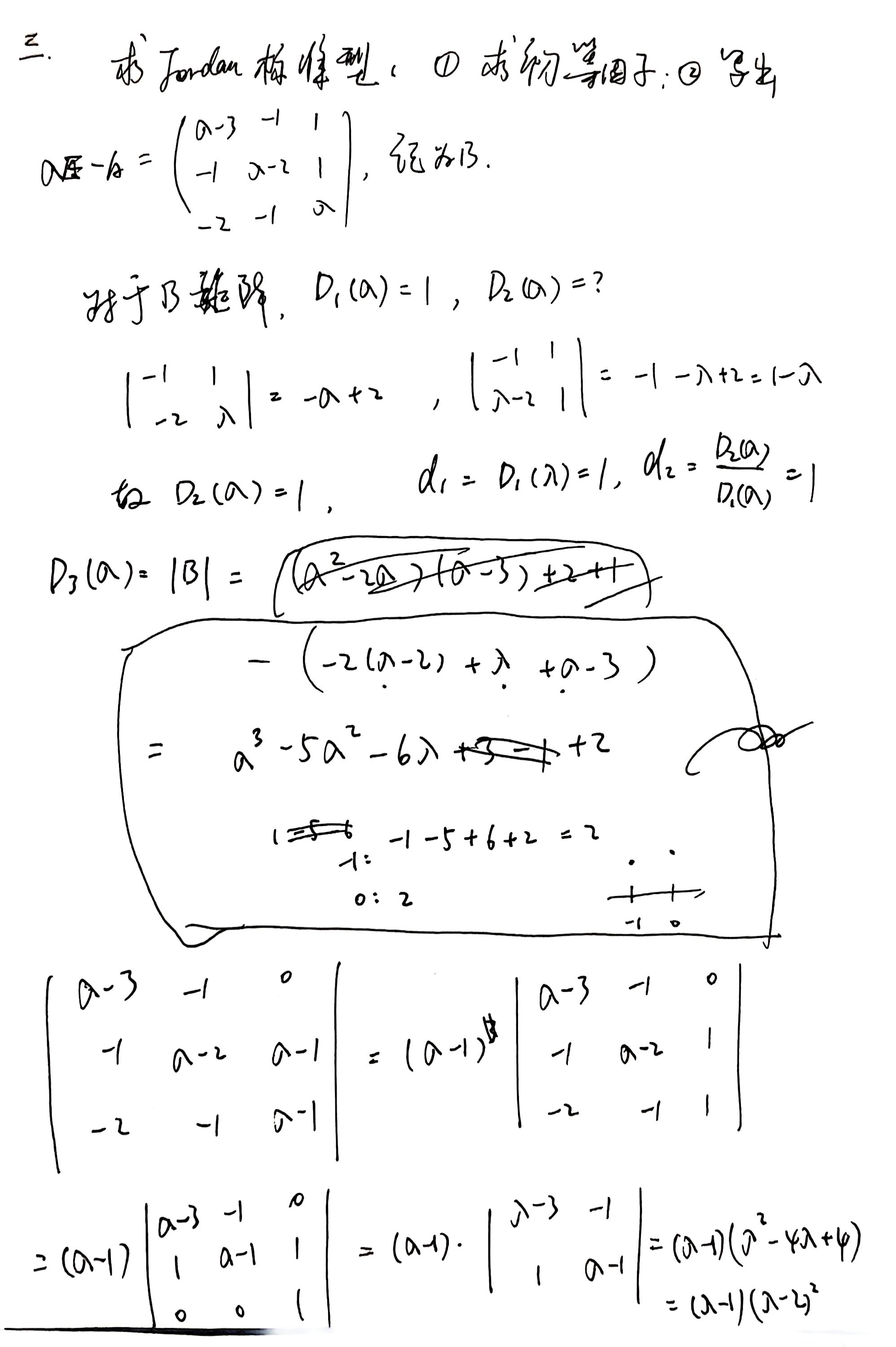
Jordan 标准形 47
凯莱-哈密顿定理 59
零化多项式、最小多项式 61
常系数线性微分方程组 73
矩阵的高次幂（Jordan标准型法） 76
矩阵函数的幂级数定义 77
利用若尔当标准型求矩阵函数 83
矩阵函数的一般定义与计算 85
一阶常系数微分方程组的初值问题 91
n 阶常系数线性微分方程 97

数值分析

数值分析（上）：

目录
数值分析的研究对象和特点 1
误差的来源与分类（模型误差、观测误差、截断误差、舍入误差、有效数字） 5
减少误差的原则 17
数学问题的稳定性、病态良态 23
数值稳定性 29
迭代法的构造 36
迭代法的收敛性与收敛速度 42
事后估计、事前估计 48
平均收敛速度 51
渐近收敛速度 52
雅可比迭代公式 54
高斯-赛德尔公式 55
SOR 迭代法 60
迭代法的矩阵表示 62
非线性方程的数值解法 75
二分法 79
试位法 83
不动点迭代 88
迭代法的收敛性（利普希茨常数、…） 91
p 阶收敛 99
艾特金加速法 104
斯蒂芬森迭代法 106
牛顿（Newton）迭代法 114
牛顿迭代法的收敛性 119
牛顿迭代法的重根处理（…、弦截法） 123
解非线性方程组的迭代法 131
不动点迭代法 134
牛顿迭代法 138

数值分析（下）：

目录
第五章数值逼近方法和数值微积分
插值问题与插值多项式 4
插值余项与误差估计 11
线性插值与二次插值 17
拉格朗日插值 20
均差与牛顿插值公式 31
Runge 现象 50
埃尔米特插值 52
埃尔米特插值的拉格朗日型插值基函数法 54
牛顿型 Hermite 插值 60
连续函数的最佳平方逼近 66
===> 问题的提法与求解 70
===> 基于幂函数的最佳平方逼近 84
===> 基于正交多项式的逼近函数类 88
===> 五种重要的正交多项式 91
数值求积公式及代数精度 107
插值型求积公式 113
Newton-Cotes公式 116
复化求积公式 124
龙贝格求积法 134
高斯型求积公式（高斯-勒让德公式、高斯-切比雪夫求积公式 …） 148
数值微分 160
泰勒展开法求数值微分 162
用插值多项式函数求数值微分 167
将数值微分转化为求数值积分 175
第六章常微分方程的数值解法
欧拉法 186
梯形法 193
预估校正法（改进欧拉法） 197
单步法的误差分析和稳定性
===> 整体截断误差和局部截断误差 198
===> 收敛性和整体截断误差 204
===> 稳定性 207
龙格库塔方法 214
标准四阶 R-K 方法的绝对稳定区域 229
变步长的龙格—库塔方法 231
线性多步法 233
预估-校正算法 243
多环节的 Adams 预估－校正公式 246

运筹学

目录
线性规划问题及其数学模型 1
单纯形法原理 5
单纯形法计算步骤 12
单纯形法的进一步讨论（人工变量、两阶段） 16
线性规划的对偶问题 21
对偶问题的基本性质 26
===> 单纯形法计算的矩阵描述 27
===> 对偶问题的基本性质 29
影子价格 31
对偶单纯形法 33
灵敏度分析 36
非线性规划的基本概念 44
无约束极值问题 50
约束极值问题 56
===> 最优性条件 56
===> 制约函数法 73